字典树<算法>

一，思想

试想一下，你查一个单词比如说book，那么你在字典中，先翻到b开头的部分，在翻到b这一段o开始的部分，依次类推，直到找到book这个单词，如果你不小心看错了一个字母，比如book你看成了boak,那么显然你查找到字母a后，查找不下去了，或者是查找到错误的单词，字典树，就是描述的上述过程。

---

举个栗子：

六个单词：an,am,and,math,mac,ok那么字典树如下：

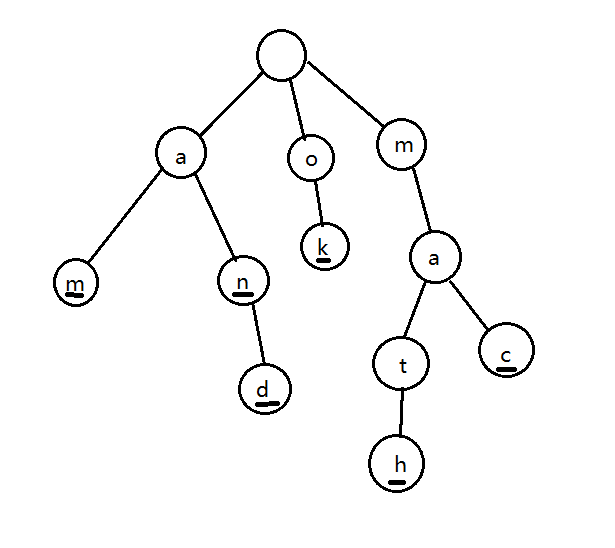
每个单词结束时给个标记，比如下面画一个短横线。

二，用途

• 字符串索引，查找。
• 统计单词个数（只需要在单词结束标记处增加一个计数即可）。
• 前缀匹配，这个很像linux下命令一样，你只需要输入前面几个字母，按tab键即可补全命令。
• 字符串排序（按照字典顺序插入，前序遍历字典树即可）。

三，复杂度

• 暴力匹配复杂度：逐个匹配复杂度为O(mn),m为字符串平均长度。
• 字典树，插入和查找都时O(m),m为插入字典树的单词的长度。

四，实现

树结构来实现

#include <iostream>
#include <string.h>
using namespace std;


struct Trie{
    Trie* next[26]; // 一个节点只会出现26个字母26种情况
    int num;    // 记录以当前字符串为前缀的单词数量
    Trie(){
        for(int i = 0; i < 26; i++)
            next[i] = NULL;
        num = 0;
    }
};

Trie root; // 根节点
void Insert(char str[]){
    // 将字符串插入字典树中
    Trie *p = &root;
    for(int i = 0; str[i]; i++){
        if(p->next[str[i]-'a'] == NULL){   // 如果当前字符没有对应的节点则创建一个
            p->next[str[i]-'a'] = new Trie; // 创建一个新的节点
        }
        p = p->next[str[i]-'a'];
        p -> num++;
    }
}

int Find(char str[]){
    // 查找以str为前缀的单词数量
    Trie *p = &root;
    for(int i = 0; str[i]; i++){    // 从第一个字母开始从顶向下依次查找
        if(p->next[str[i]-'a'] == NULL){    // 如果当前节点没有这个单词中的当前位置的字母则查找失败
            return 0;
        }
        p = p->next[str[i]-'a'];
    }
    return p->num;  // 返回当前单词结尾处的前缀数量
}

数组实现(更紧凑的代码)

int trie[10005][26];    // 数组定义字典树，存储下一个字符的位置
int num[10005] = {0};   // 统计某一个字符串为前缀的数量
int pos = 1;    // 当前新分配的存储位置

void Insert(char str[]){
    int p = 0;
    for(int i = 0; str[i]; i++){
        int n = str[i] - 'a';
        if(trie[p][n] == 0){    // 当前节点没有值
            trie[p][n] = pos++; // 为了在num数组中更好的记录前缀出现的次序
        }
        p = trie[p][n];
        num[p] ++;
    }
}

int Find(char str[]){
    int p = 0;
    for(int i = 0; str[i]; i++){
        int n = str[i] - 'a';
        if(trie[p][n] == 0){
            return 0;
        }
        p = trie[p][n];
    }
    return num[p];
}

五，应用

查找一组单词中，以某个词为前缀的单词有多少个

int main()
{
    char str[11];
    while(gets(str)){
        if(!strlen(str)) break; // 输入空行则跳出去
        Insert(str);
    }
    while(gets(str)) cout << Find(str) <<endl;
    return 0;
}

输出结果：

am
and
ok
math
mac // 输入结束

ma
2
a
2
and
1
c
0

注： 当然解决该问题，map为一个不错的方法，只需定义map<string, int> m 将单词插入时，只需要m[str]++即可。