1. 首先来说拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。
该序列必须满足下面两个条件:
第一:每个顶点出现且只出现一次。
第二:若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
当然有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
例如,右边这个图: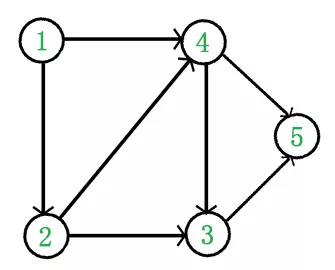
它是一个 DAG 图,那么如何写出它的拓扑排序呢?
2. 怎么求拓扑排序。
思路一:从 DAG 图中选择一个 没有前驱(即入度为0)的顶点并输出。从图中删除该顶点和所有以它为起点的有向边。
重复这两个动作直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
于是,上图得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。
但是要注意:一个图的拓扑排序得到的结果可能存在多个
这次算法也就是我们经常说到的Kahn算法。
给个例题吧:UVA - 10305

利用我们的Kahn算法来写就是如下:
#include <iostream>
#include <stdio.h>
#include <string>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n,m;
int a,b;
vector<int>v[maxn];
int indrgee[maxn];
int order[maxn];
queue<int>q;
void toposort()
{
for(int i=1;i<=n;i++)//找到初始情况下入度为0的点
{
if(indrgee[i]==0)
q.push(i);
}
int cnt=0;
while(!q.empty())
{
int temp=q.front();
q.pop();
order[cnt++]=temp;
int len=v[temp].size();
for(int i=0;i<len;i++)
{
indrgee[v[temp][i]]--;
//每次删去该顶点和所有以它为起点的有向边故对应点的入度减一,如果为0,就放入队列
if(indrgee[v[temp][i]]==0)
q.push(v[temp][i]);
}
}
printf("%d",order[0]);
for(int i=1;i<cnt;i++)
printf(" %d",order[i]);
printf("
");
}
int main()
{
while(scanf("%d %d",&n,&m)!=EOF)
{
if(n==0&&m==0)
break;
while(!q.empty())
q.pop();
for(int i=0;i<=n;i++)
{
v[i].clear();
indrgee[i]=0;
}
while(m--)
{
scanf("%d %d",&a,&b);
v[a].push_back(b);
indrgee[b]++;//对应的入度加1.
}
toposort();
}
return 0;
}
思路二:
首先我们讨论一下拓扑排序的性质,对于一个图,它可能会有好几种拓扑排序,但他们同时满足一个规律,那就是如果存在有向边u->v, 那么结点u必须排在v之前(前驱)。同时这种性质具有传递性,也就是说如果同时存在v->t, 那么满足u在t之前。同样的,如果u和v两个结点在图中并不满足这种性质,那么谁在前谁在后就无所谓了。正是利用这个规则,我们进行dfs的顺序是无所谓的。
为何?因为我们从root结点开始dfs一遍,可以找到所有的必须在这个root结点之后的点,那么我们就满足了拓扑序的规则了,那么我们无论先dfs(u)还是先dfs(v), 都不会违背这个规则(除非有环),那么同时我们只要按照某种合理的方式存储所有这些点,那么他们就是拓扑序了。
什么是合理的方式?栈!考量一个dfs(u), 在它结束该退出时,它代表它的结点u。在dfs递归中,什么点会最先exit?没有后继结点的点(或者后继已入栈的点)!那么把所有点分成两个集合,一个是待处理的点集D,一个是已拓扑排序后的点集A,当且仅当D中某个点没有后继结点(或该后继结点已经加入了点集A中)时,它可以从D转移到A,而dfs的回溯方式,恰恰就自动实现了这样的功能。
那么上面的那个例题用dfs来写的话就是
#include <iostream>
#include <stdio.h>
#include <string>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
const int maxn=105;
int n,m;
int a,b;
bool G[maxn][maxn];
int vis[maxn];
int order[maxn];//代替栈,每次插入插到拓扑排序首位
int len;
//用vis数组,vis[u]=0表示从来没访问过,vis[u]=1表示已经访问过了,vis[u]=-1表示
//正在访问,即递归调用还在进行,尚未返回。
bool dfs(int u)
{
vis[u]=-1;
for(int v=1;v<=n;v++)
{
if(G[u][v])
{
if(vis[v]<0)
return false;
else if(!vis[v]&&!dfs(v))
return false;
}
}
vis[u]=1;
order[--len]=u;
return true;
}
bool toposort()
{
len=n;
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
{
if(!vis[i])//如果没有被访问过
{
if(!dfs(i))//如果没有还
return false;
}
}
return true;
}
int main()
{
while(scanf("%d %d",&n,&m)!=EOF)
{
if(n==0&&m==0)
break;
memset(G,0,sizeof(G));
while(m--)
{
scanf("%d %d",&a,&b);
G[a][b]=true;
}
toposort();
printf("%d",order[0]);
for(int i=1;i<n;i++)
printf(" %d",order[i]);
printf("
");
}
return 0;
}