1. LeetCode - 98. Validate Binary Search Tree (判断一颗二叉树是不是一颗二叉搜索树)
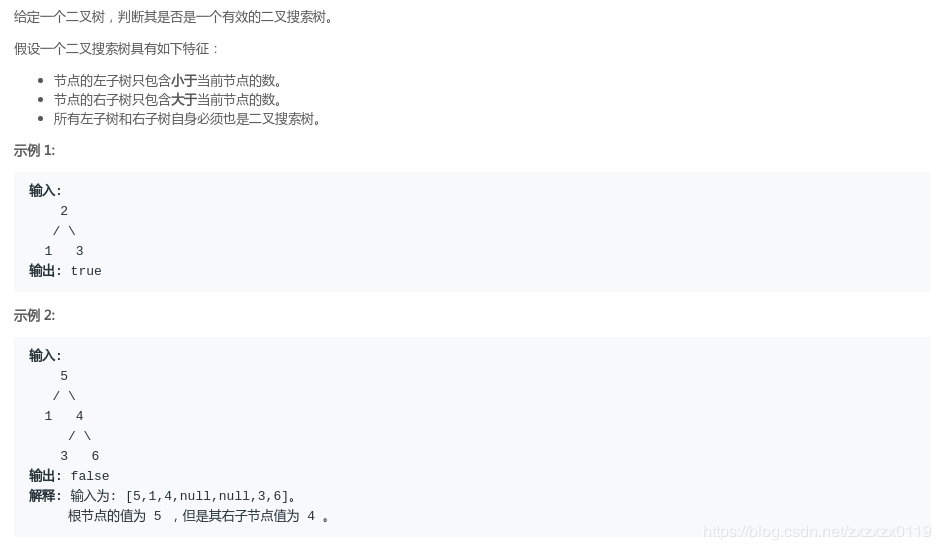
什么是二叉搜索树?任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
根据性质怎么判断一颗二叉树是不是搜索二叉树呢? 其实很简单,只要这颗二叉树的中序遍历的顺序是升序的,那么就是一颗二叉搜索树,因为中序遍历的顺序是左->中->右,所以当中序遍历升序的时候,就有左<中<右,所以就可以判断。
class Solution {
public boolean isValidBST(TreeNode root) {
if(root == null)
return true;
Stack<TreeNode>stack = new Stack<>();
TreeNode cur = root;
TreeNode pre = null;
while(!stack.isEmpty() || cur != null){
if(cur != null){
stack.push(cur);
cur = cur.left;
}else {
cur = stack.pop();
if(pre != null && cur.val <= pre.val)
return false;
pre = cur;
cur = cur.right;
}
}
return true;
}
}
2. 判断一个二叉树为完全二叉树
判断过程:
1.按照层次遍历的顺序遍历二叉树,每一层从左到右;
2.如果当前结点有右孩子但没有左孩子,直接返回false;
3.如果当前结点不是左右孩子都全(包括两种情况),那之后的结点必须都为叶节点,否则返回false;
4.遍历过程中如果没有返回false,就返回true;
//判断一棵二叉树是不是完全二叉树
static boolean isCBT(TreeNode root){
if(root == null)
return true;
Queue<TreeNode>queue = new LinkedList<>();
boolean leaf = false; //如果碰到了 某个结点孩子不全就开始 判断是不是叶子这个过程
queue.add(root);
TreeNode top = null,L = null,R = null;
while(!queue.isEmpty()){
top = queue.poll();
L = top.left; R = top.right;
//第一种情况
if((R != null && L == null))
return false;
//第二种情况 开启了判断叶子的过程 而且又不是叶子 就返回false
if(leaf && (L != null || R != null)) //以后的结点必须是 左右孩子都是null
return false;
if(L != null)
queue.add(L);
//准确的说是 只要孩子不全就开启leaf,
//但是前面已经否定了有右无左的情况,这里只要判断一下右孩子是不是为空就可以了(如果为空就开启leaf)
if(R != null)
queue.add(R);
else
leaf = true;
}
return true;
}
3. 判断一棵树是否为二叉平衡树
解决方法:从根节点开始,先判断左右子树的高度差是否超过1,然后接着判断左右子树是否是平衡二叉树。这边用到了递归思想。
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if( root == null) { //一棵空树就是平衡二叉树
return true;
}
if( Math.abs(getDepth(root.left) - getDepth(root.right)) <= 1 ) {
//满足左右子树高度差小于等于1,那就接着判断左右子树是不是二叉树
return (IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right));
} else {
//不满足左右子树高度差小于等于1,那这棵树肯定不是平衡二叉树啦
return false;
}
}
public int getDepth(TreeNode root) {
if( root == null ) return 0;
int left = getDepth(root.left);
int right = getDepth(root.right);
return ( left > right ? left : right ) + 1;
}
}