1. 红黑树是在二叉查找树的基础上延伸的。先看下二叉查找树。定义是:它不为空树时,它左子树上所有的元素都小于根节点的元素,而根节点右子树上所有的元素都大于根节点的元素。可以看下图(扒来的)
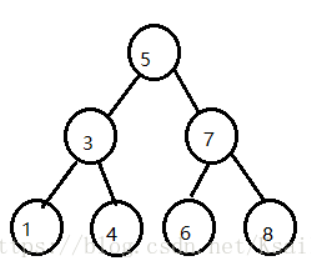
2. 为了保证二叉查找树不失衡(出现线性查找的情况),就有了平衡的二叉查找树:红黑树。
它除了满足二叉查找树的特征还满足:节点是红色或者黑色;根节点是黑色;每个红色节点的儿子都是黑色的(红节点不能连续);从任一节点到其每个叶子的路径包括个数相同的黑色节点。
插入一个元素到红黑树的时间为log(N);采用迭代器遍历一棵红黑树的时间复杂度是O(N)
如图:
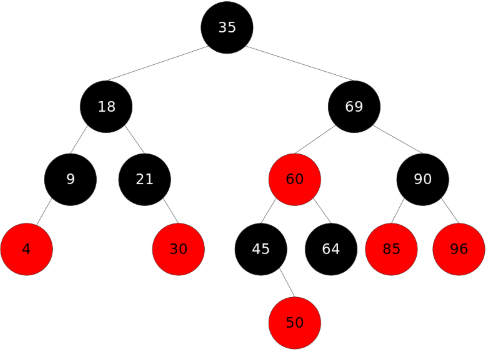
3. 红黑树的插入
1.如果插入的节点是根节点,也就是说初始的红黑树为空,这是最简单的情况,直接将该节点标识成黑色即可。
2.如果新插入的节点不是红黑树的根节点,如果新插入的节点的父节点是黑色的话,那么红黑树是不需要调整的
3.如果新插入的节点的父亲P和叔叔U都是红色的情况。这时,将P、U都染成黑色,而G染成红色以满足性质5(从任一节点出发到其每个叶子节点的路径,黑色节点的数量是相等的)。现在,当前的红色节点N有一个黑色的父亲,而且所有经过父亲和叔叔节点的路径仍然保持与原来相同的节点个数。但是爷爷节点G可能会违反性质2(根节点必须是黑色)或者性质4(红色节点必须有两个黑色儿子节点)(在G节点的父亲也是红色节点时,会破坏性质4)。要修复这个问题,可以对节点G递归执行Case1的操作
4.父亲P是红色,叔叔U是黑色,并且N是P的右孩子,P是G的左孩子的情况。这时,对节点P执行左旋操作,使P变成N的左孩子,N变成G的左孩子,也就是说进入了5 的情况。
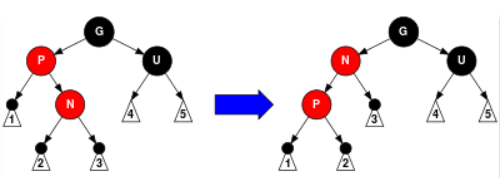
5.父亲P是红色,但叔叔U是黑色, N是左孩子,P也是左孩子的情况。此时,对节点G执行一次右旋。使P成为N和G的父节点。已知G是黑色(P是红色,为了不破坏性质4(红色节点必须有两个黑色儿子节点),G肯定是黑色),所以将G染成红色,P染成黑色。
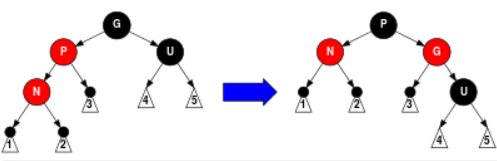
4. 红黑树的删除
看这个吧:https://www.cnblogs.com/zutterhao/p/7535878.html