在一年前赢得了小镇的最佳草坪比赛后,FJ 变得很懒,再也没有修剪过草坪。
现在,新一轮的最佳草坪比赛又开始了,FJ 希望能够再次夺冠。
然而,FJ 的草坪非常脏乱,因此,FJ 只能够让他的奶牛来完成这项工作。
FJ 有 N 只排成一排的奶牛,编号为 1 到 N。
每只奶牛的效率是不同的,奶牛 i 的效率为 Ei。
编号相邻的奶牛们很熟悉,如果 FJ 安排超过 K 只编号连续的奶牛,那么这些奶牛就会罢工去开派对。
因此,现在 FJ 需要你的帮助,找到最合理的安排方案并计算 FJ 可以得到的最大效率。
注意,方案需满足不能包含超过 K 只编号连续的奶牛。
输入格式
第一行:空格隔开的两个整数 N 和 K;
第二到 N+1 行:第 i+1 行有一个整数 Ei。
输出格式
共一行,包含一个数值,表示 FJ 可以得到的最大的效率值。
数据范围
\(1≤N≤105,\)
\(0≤Ei≤109\)
输入样例:
5 2
1
2
3
4
5
输出样例:
12
样例解释
FJ 有 5 只奶牛,效率分别为 1、2、3、4、5。
FJ 希望选取的奶牛效率总和最大,但是他不能选取超过 2 只连续的奶牛。
因此可以选择第三只以外的其他奶牛,总的效率为 1 + 2 + 4 + 5 = 12。
思路
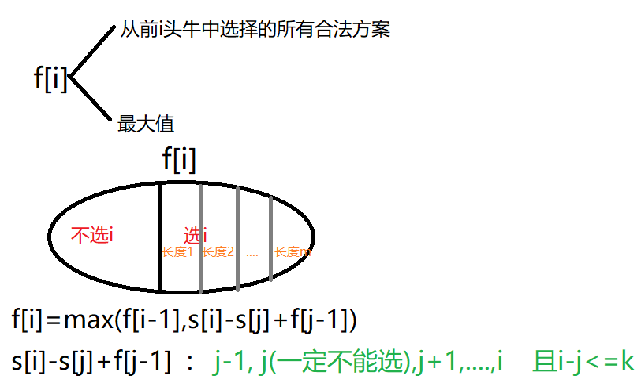
求f[i]时,s[i]是定值,f[j-1]-s[j]在j合法的范围内最小,这个值可以通过滑动窗口来维护。
代码
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N=100010;
LL f[N],s[N],q[N];
int main(int argc, char * argv[])
{
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;++i) cin>>s[i],s[i]+=s[i-1];
int hh=0,tt=0;
LL res=0;
tt++;
for(int i=1;i<=n;++i){
f[i]=f[i-1];
if(hh!=tt && i-q[hh]>m) hh++;
f[i]=max(f[i],f[max(0ll,q[hh]-1)]-s[q[hh]]+s[i]);
while(hh!=tt && f[max(0ll,q[tt-1]-1)]-s[q[tt-1]]<=f[i-1]-s[i]) tt--;
q[tt++]=i;
res=max(f[i],res);
}
cout<<res<<endl;
return 0;
}