一、深度学习
定义:深度学习是为了能够得到有助于理解图片、声音、文本等的数据所表述的意义而进行的多层次的表示和抽取的学习。用简单的机器学习,例如用含2个或3个隐含层的神经网络,是不可能达到与人类类似的判别决策的。这就需要多层的学习器,逐层学习并把学习到的知识传递给下一层,以便下层能够得到更高级别的表述形式,期望可以得到与人类类似的结论。
学习的深度
学习器的深度,决定于学习器的构造。根据学习的深度,机器学习可以分为浅度学习和深度学习。假设学习器为一个有向流通图,那么深度就是从开始结点到结束结点的最长路径。例如,一个支撑向量机的深度是2,是输入经过一个核变换到核空间,再加上一个线性组合。再如多层前传神经网络的深度是隐含层层数加1(输出层)。如果说学习到一次知识,就是一个深度的话,那么学习的深度是原始数据被逐层学习的次数。
二、深度学习的方法
深度监督学习:卷积神经网络(Convolutional Neural Nets,CNNs)
深度非监督学习:深度置信网(Deep Belief Nets,DBNs)
2.1 卷积神经网络:非全连+权值共享+子采样→降低BP网复杂度
卷积神经网络是一种非全连接的BP神经网络,在最前面加了2种特征抽取结构:卷积层和子采样层。
1)非全连(减参):全连接网络学习100x100的图像提取100个特征,需要10^4个输入单元并学习10^6个参数。因此采用非全连结构,神经元只学习局部特征最后组合。
2)卷积层(特征抽取):。用模板(滤波器)fx去卷积输入图像(之后为特征图),加上偏置bx,得到卷积层cx。


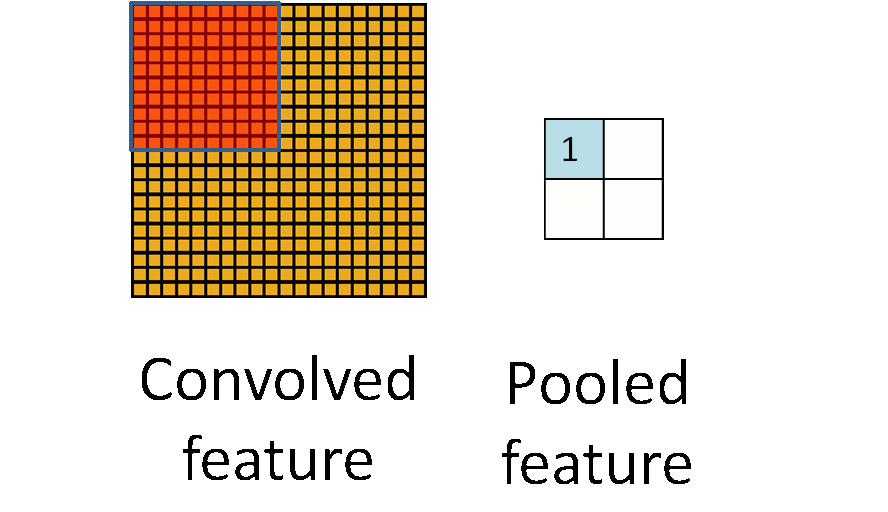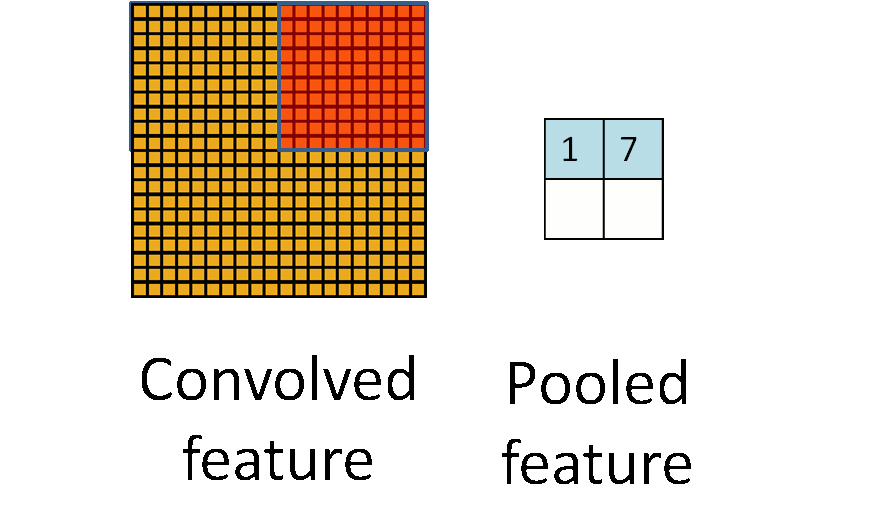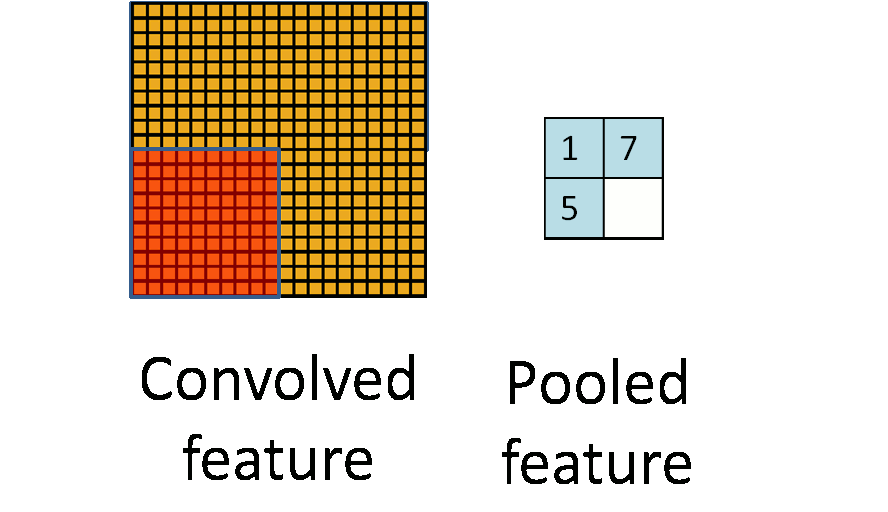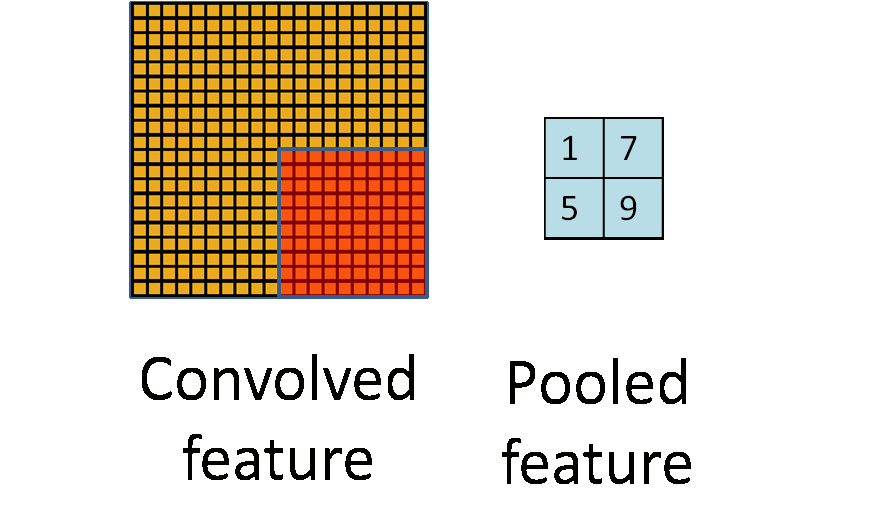
3)子采样(池化):减少学习参数(由n*(|f|^2+1)个参数变为n*(1+1)个参数)。每领域四个像素求和,通过Wx+1加权并加上偏置bx+1,最后通过sigmoid激活函数产生缩为1/4的特征图Sx+1。
上图中:c1层用6个5x5模版卷积原始32x32图像得到6个28x28图像;s2层进行模糊滤波减参;c3层是s2层特征图的组合,再用16个5x5模板分别去卷积;s4层进行1/4模糊滤波减参;c5层是s4层的全组合(16*15/2),再用1个5x5模板去卷积,得到120个1x1特征图;F6为隐层神经元,与c5层全相连,计算输入向量与权重向量的点积;O7为径向基单元输出层,每个RBF单元计算输入向量与参数向量的距离,目标最小化距离。
实例:LeNet模型(用于识别手写/机打字体等多类图形)
输入层后有2组隐含层抽取输入图像的特征,最后有一个全连接的隐含层完成对输入图像的识别。LeNet模型抗噪能力很强,用传统的BP进行训练。
2.2深度置信网
DBNs是多个RBM的累加。Boltzmann机是基于能量理论的概率模型,通过能量函数定义概率分布:Boltzmann分布。设随机变量x,能量函数E(x),则该状态出现的概率分布密度函数为p(x)=exp(-E(x))/Z,其中Z=Σexp(-E(x))。典型的Boltzmann机是一个无向循环图,其能量函数定义为:
其中x是可见变量,可以观察到实际数据;h是隐含变量,无法观察到实际值;b和c分别是可见变量和隐含变量的系数;W,U,V是结点间的连接权重,若对Boltzmann机加约束(RBM),令其不能自身链接,则得到一个有向无环图,其能量函数定义为:
一个典型的置信网可以看成是由多个随机变量组成的有向无环图,也可以看成是多个RBM的累加,而深层置信网就是一个复杂度很高的有向无环图。一个有L个隐含层的典型的DBN,可以用联合概率分布刻画输入向量x和隐含向量h的关系
DBN学习的过程,就是学习联合概率分布(产生式模型)的过程。RBM深度学习模型如下:
通过一个非监督贪婪逐层方法去预训练获得生成模型的权值。在此训练阶段,可视层会产生一个向量v,通过它将值传递到隐层。反过来,可视层的输入会被随机的选择,以尝试去重构原始的输入信号。最后,这些新的可视神经元将前向传递重构隐层,获得h(在训练过程中,首先将可视向量值映射给隐单元;然后可视单元由隐层单元重建;这些新可视单元再次映射给隐单元获取新的隐单元,即Gibbs采样)。这些后退和前进的步骤就是Gibbs采样,而隐层激活单元和可视层输入之间的相关性差别就作为权值更新的主要依据。