一、背景
Python中提供了List用于存储一组数据

但是由于机器学习中类型大多一致,List每次都需要判断各个数据的类型,性能较低。
Python中又提供了Array类型
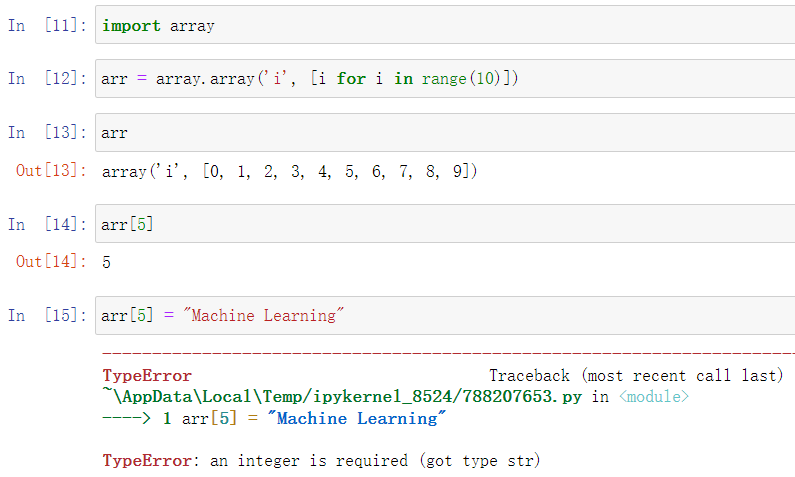
但由于机器学习中大多为向量的计算,array并没有兼顾此方面。
因此以上两种结构都不适用于机器学习的数据存储,故引入了Numpy模块,其支持大量的维度数组与矩阵运算。
二、模块导入及简单演示
使用import导入Numpy模块,由于经常调用可以为其取别名np
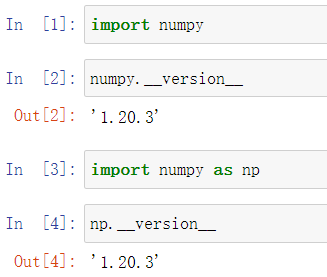
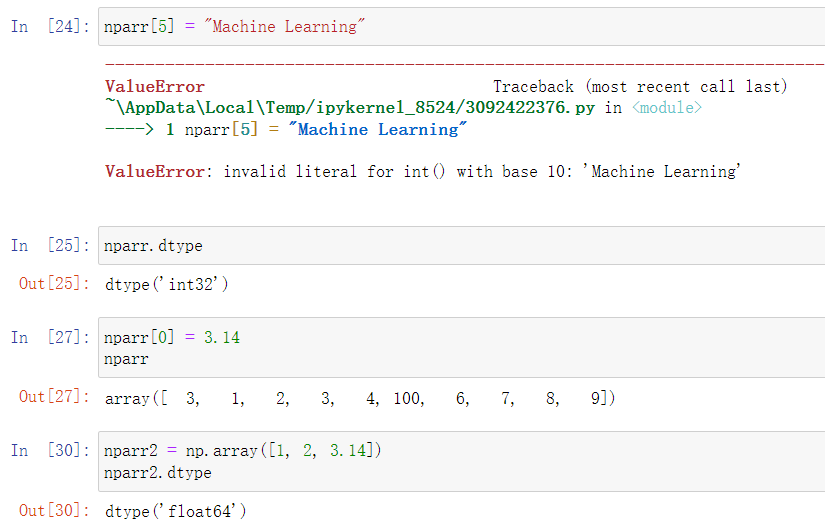
同样,numpy.array只支持同类型数据的存储

当赋予其他类型的数据时可能会报错,也可能会发生隐式转换
三、创建数组和矩阵
1.zeros,ones,full
numpy中提供了方法zeros用于创建一个全为0的数组
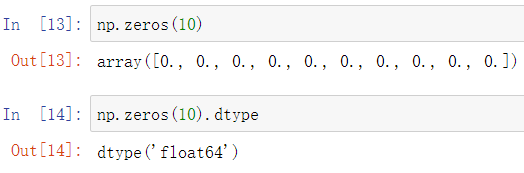
由此可见,numpy.array的默认数据类型64位浮点型
此外,可以设置dtype参数指定数据类型

通过传入元组,可以创建矩阵,如下3行5列矩阵

numpy还提供了ones方法用于创建全为1的数组

若要为数组指定某个其他值,可以使用full方法

2.arange
在Python中提供了range方法

同样的,numpy中也有一个类似的方法arange,不同之处在于其步长可以为小数

3.linsapce
此外,numpy还提供了linsapce方法,其第三个参数为等长截取的数据的个数(如下分别截取成10、11个)

4.random
numpy同样提供了random用于生成随机数,如使用randint生成指定范围内的随机整数
同样地,可以为其指定size以生成向量和矩阵

通过seed方法指定随机种子,可以保证每次随机生成相同的数据

调用random方法可以随机生成 [0, 1) 间的随机数,并传入参数生成指定大小的向量和矩阵
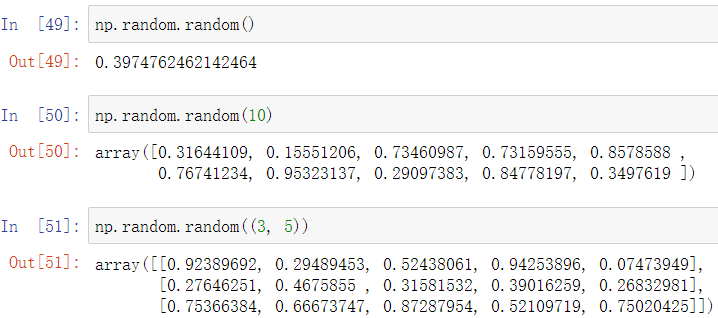
若要随机数符合正态分布,则可以使用normal方法
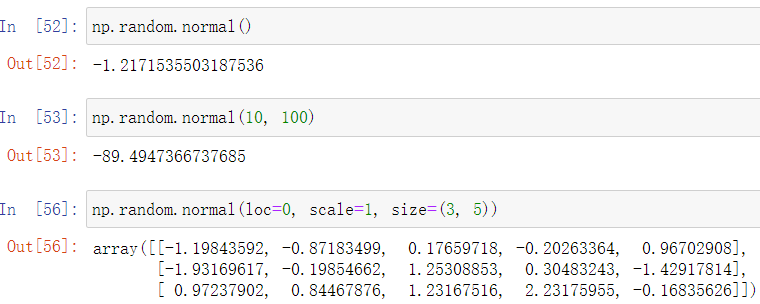
如上面生成符合平均数为0,标准差为1的正态分布的随机数组成的3行5列矩阵
注:若要查看方法参数,Jupyter Notebook中使用?或者help()
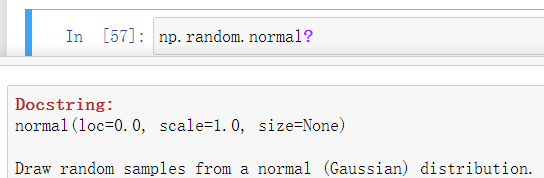
四、数组的基本操作
1.基本属性
现有如下两个数组x和X

ndim:获取数组的维数

shape:获取数组行列数

size:获取数组大小
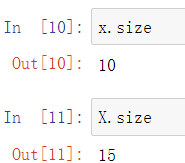
2.数据访问
和Python的List相同,numpy.array同样支持索引访问数据
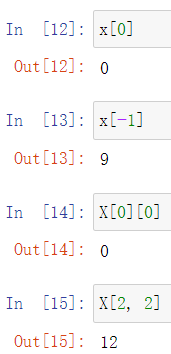
注意:当使用索引访问矩阵时,建议使用传入元组 (i ,j) 的形式访问,括号可省略,如X[2, 2],不建议使用X[i][j]的形式
在访问数据时,同样支持List的切片操作

可以发现,若使用X[i][j]的形式,将会先截取前两行,再截取该两行数据的前三行,显然不是想要的前两行三列
若要访问矩阵的某一行,如下:

若要访问矩阵的某一列,如下:
![]()
注意:与Python的List不同,由numpy数组生成的子数组是同一个对象引用,修改其中一个,另一个也会随之更改

若要将其区分为两个独立的对象,则使用copy方法

通过调用reshape方法,可以转换矩阵的行列数

若想让其智能地转为n行或n列的矩阵,则可将另一个行或列参数赋为-1

注意:输入的行数或列数必须能被总数整除
五、数组的合并与分割
1.合并操作
使用concatenate方法合并数组
假设现有两个numpy数组
![]()
通过传入数组列表的方式,可以将多个数组进行合并
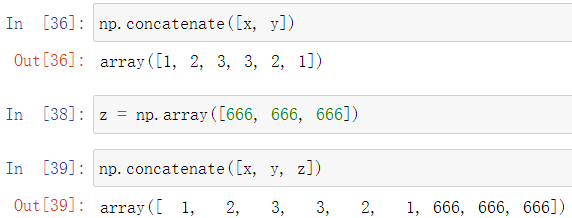
同样,可以对矩阵进行合并,并使用axis指定合并的方向(默认为0,对行合并;1为对列合并)

注意:当使用concatenate时,传入的矩阵必须拥有相同的维数,若要将向量合并到矩阵,需要先使用reshape方法转为矩阵

此外, numpy提供了更加便捷的vstack和hstack方法实现垂直、水平方向的合并,且直接适用于向量

2.分割操作
使用split方法实现数组的分割,通过传入list的形式指定分割点的索引

在对矩阵进行分割时,应当区分垂直或水平分割(默认为0,对行分割;1为对列分割)

同样numpy提供了更便捷的方法vsplit和hsplit方法,进行垂直、水平方向上的分割

适用场景:机器学习中通过数组的形式,传入其特征feature和标记label,如下面的data,前三列为样本特征,最后一列为标记,则可以使用hsplit对其分割
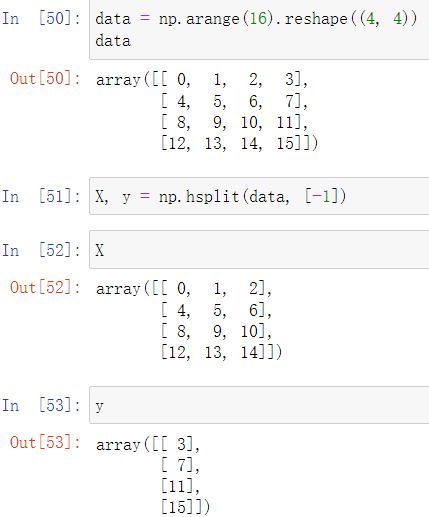
一般标记以向量的形式表示,如下获取标记向量
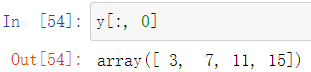
六、矩阵运算
1.引入
在Python中提供了以下方式实现对list中元素的计算
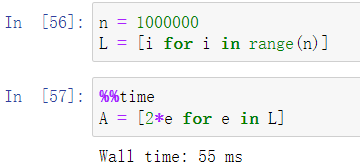
同样,numpy中也可以使用列表推导式实现,且更高效
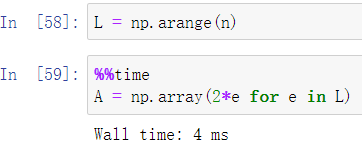
此外,numpy还提供了更简洁的直接运算,且效率较前者更高
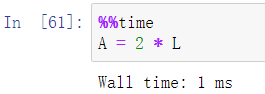

2.基本数学运算
对于矩阵,numpy实现了大量的基本运算
如:加减乘除、地板除
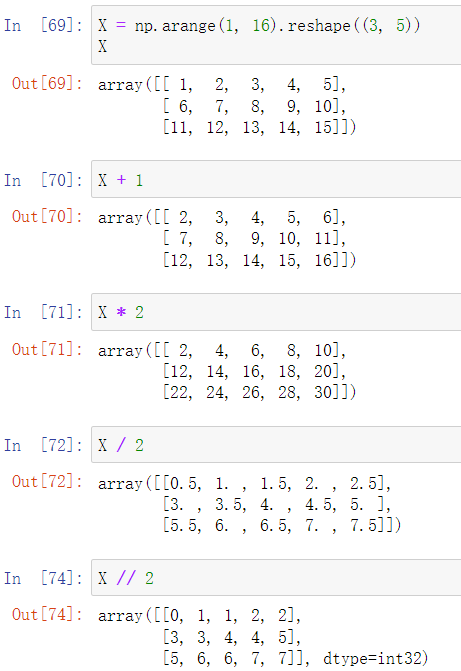
如:幂运算(power或**),模运算


如:取倒数,绝对值,三角函数等等
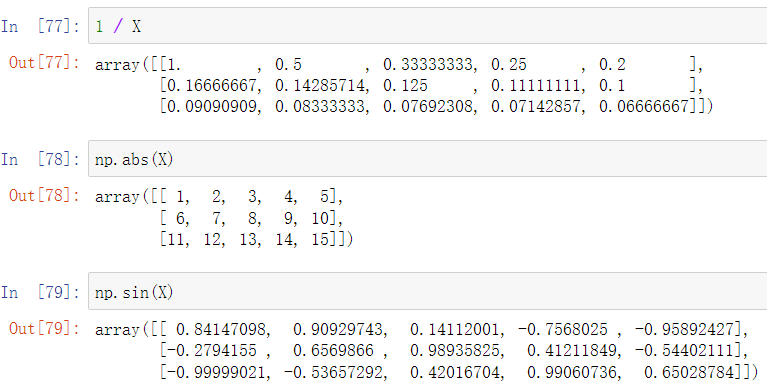
如:对数运算(log,log2,log10)

3.矩阵间的运算
注意:下列运算都是对矩阵中的每个数据一一对应的分别运算
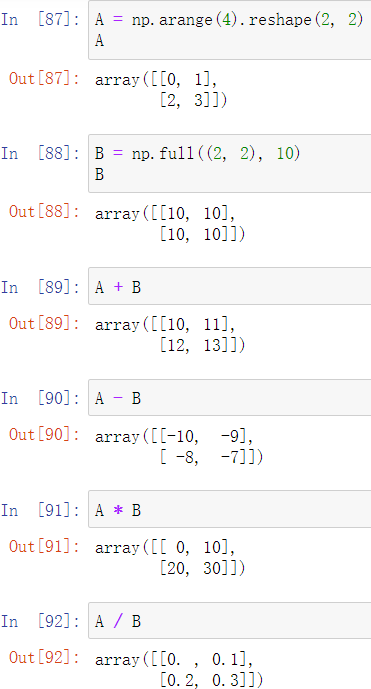
若要获取矩阵的积(前行乘后列,设A为m*p的矩阵,B为p*n的矩阵,则A与B的乘积为m*n的矩阵),应调用dot方法

获取矩阵的转置(行列互换),调用属性T
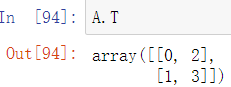
4.向量与矩阵的运算
numpy支持向量与矩阵的直接运算
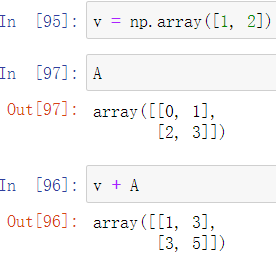
这在线性代数中是不合理的,若要满足线性代数计算方式,同理等价为:先将向量堆叠再计算

实现向量的堆叠,numpy提供了更直接的tile方法,如下:将向量行方向堆叠2次,列方向堆叠1次

向量与矩阵的积同样使用dot方法,注意:dot方法会根据向量v的前后位置自动判断为行向量或列向量

调用np.linalg.inv方法可以求得逆矩阵,注意:只有方阵才存在逆矩阵,二者乘积为单位矩阵

在机器学习中经常需要求逆,即便该矩阵不是方阵,此时可以调用np.linalg.pinv获取伪逆矩阵,二者乘积也为单位矩阵(主对角线之外的数不为零是由计算机精度引起的)
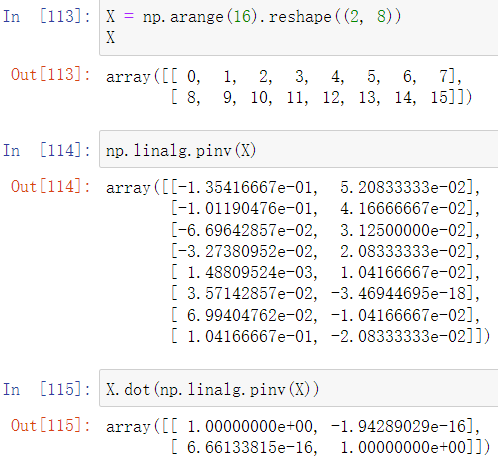
七、聚合运算
所谓聚合运算可以理解为将一组值转为一个值,如求数组的和,numpy提供了一系列方法用于聚合运算
sum:求和
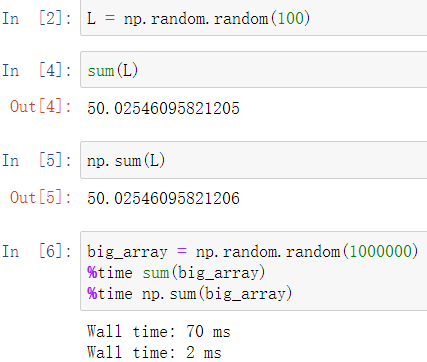
与python自带的方法相比,其效率更高
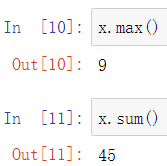
min、max:最小、最大值

这些方法也支持面向对象的方式进行调用,如:
在对矩阵进行求和运算时,其会对所有数进行累加操作

若要求某列或某行的和,则可以指定axis参数(0为行方向上求和,1为列方向上求和)

prod:获取所有数的乘积
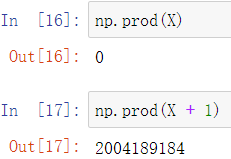
第一个结果为0是因为第一个数就是0
mean:获取平均值

median:获取中位数
![]()
注意:当存在某些脱离整体的数据时,中位数比平均值更具代表性

此时中位数2.0更能代表整体
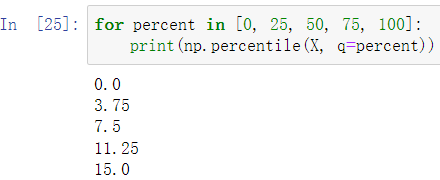
percentile:获取小于整体的指定百分比位置的数
如:X中有50%的数小于等于7.5;100%的数小于等于15,即最大值

var:求方差
![]()
std:求标准差
![]()
下面生成一个满足正态分布的随机数数组进行测试
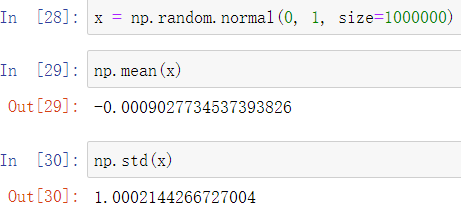
其平均值0与标准差1都与指定值一致(误差源于计算机精度问题)
八、arg索引
numpy中提供了arg一类的方法用于获取数据原索引
如min可以获取最小值,那么argmin方法就可以获取最小值的索引,argmax方法获取最大值的索引

numpy提供了sort方法进行排序,如下先初始化一个数组,并调用shuffle方法乱序化

调用np.sort获取有序化后的数组
![]()
若要将原有数组有序化,应当以面向对象的方式调用sort方法

sort方法同样适用于矩阵,设置axis参数可以指定排序的方向,默认为按列方向排序(axis=1)

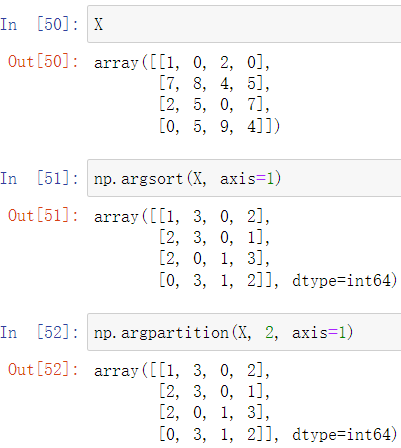
现在如果想知道获取的结果中的数据在原未排序数组中的索引,可以调用argsort方法(如:排序后的第一个数0在原数组中的索引为1)

partition方法可以按照指定数进行前后分组(小于该数的在此数前,大于的在该数后,前后分组中的数是无序的)

同样,调用argpartition可以获取在原数组中的索引

以上方法同样适用于矩阵
九、FancyIndexing与数据比较
1.FancyIndexing
之前提到, numpy数组支持索引的方式访问数据,如下:

但这只能访问某些特定规则的数据,如果要想访问任意指定的索引,numpy提供了fancyindexing,如需访问索引为3,5,8的元素,可以如下表示:

其同样支持以矩阵的形式传入索引,其结果也以矩阵的形式输出

fancyindexing同样适用于矩阵,如下指定需要访问的行和列索引

也可以传入一个bool数组,其中True表示要获取的行或列

2.数据比较
numpy数组支持直接以运算符的方式对数组中的数进行比较判断,并返回一个bool数组
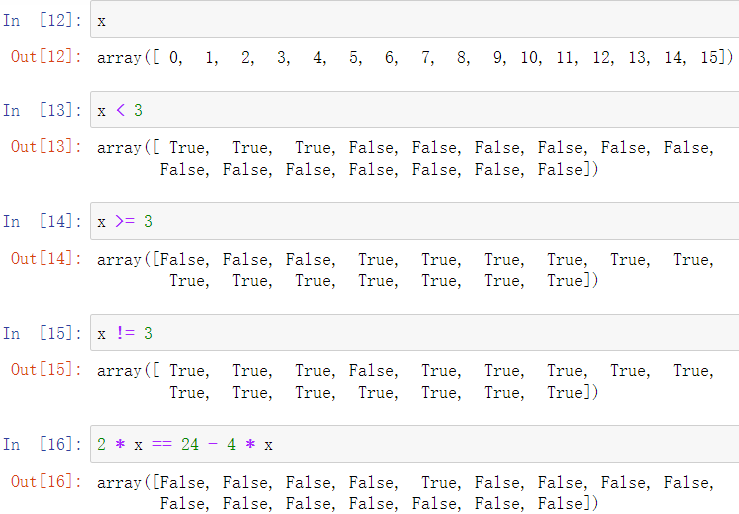
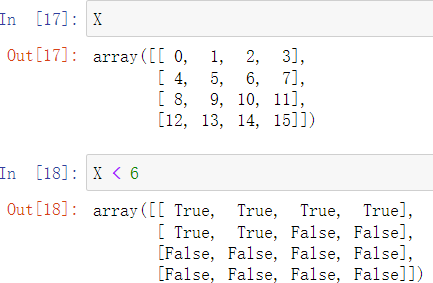
3.结合使用
由于数据比较返回的是一个numpy数组,且fancyindexing需要传入一个数组作为索引,故二者可以结合使用以获取满足特定条件的数组或数值
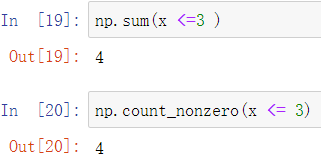
numpy提供了count_nonzero方法获取非零项总数,True即非零
使用any方法可以判断是否存在满足要求的项
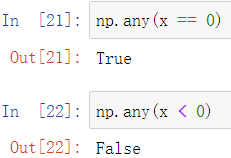
使用all方法可以判断是否所有项都满足要求
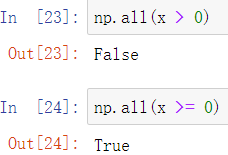
对于矩阵,可以通过参数axis指定行或列进行筛选

数据比较时支持与、或、非运算,注意:此处使用的是位运算符&,而不是条件运算符&&,这是因为运算的对象为数组,而不是布尔值

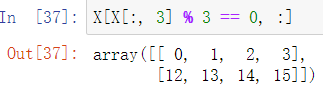
结合使用举例:获取矩阵中所有满足第4列能被3整除的行