目录:
- 定义(What)
- 判定表的四个组成部分
- 规则及规则合并
- 判定表的建立步骤(How)
- 使用场景
- 优缺点
- 实战演练
1.定义(What)
判定表是分析和表达多逻辑条件下执行不同操作的工具。它能够将复杂的问题按照各种可能的情况全部列举出来,因此,利用判定表能够设计出完整的测试用例集合。在一些数据处理问题当中,某些操作的实施依赖于多个逻辑条件的组合,即:针对不同逻辑条件的组合值,分别执行不同的操作。判定表很适合于处理这类问题。
2.判定表的四个组成部分
- 条件桩(Condition Stub):列出了问题的所有条件。通常认为列出的条件的次序无关紧要。
- 动作桩(Action Stub):列出了问题规定可能采取的操作。这些操作的排列顺序没有约束。
- 条件项(Condition Entry):列出针对它所列条件的取值。在所有可能情况下的真假值。
- 动作项(Action Entry):列出在条件项的各种取值情况下应该采取的动作。
3.规则及规则合并
- 规则:任何一个条件组合的特定取值及其相应要执行的操作称为规则。在判定表中贯穿条件项和动作项的一列就是一条规则。显然,判定表中列出多少组条件取值,也就有多少条规则,即条件项和动作项有多少列。
- 化简:就是把规则进行合并。合并的标准是,有两条或多条规则具有相同的动作,并且其条件项之间存在着极为相似的关系。
4.判定表的建立步骤(根据软件规格说明)

- 确定规则的个数。假如有n个条件。每个条件有两个取值(0,1),故有2^n种规则;
- 列出所有的条件桩和动作桩;
- 填入条件项;
- 填入动作项。等到初始判定表;
- 简化,合并相似规则(相同动作)。
5.使用场景
B. Beizer 指出了适合使用判定表设计测试用例的条件:
- 规格说明以判定表形式给出,或很容易转换成判定表;
- 条件的排列顺序不会也不影响执行哪些操作;
- 规则的排列顺序不会也不影响执行哪些操作;
- 每当某一规则的条件已经满足,并确定要执行的操作后,不必检验别的规则;
- 如果某一规则得到满足要执行多个操作,这些操作的执行顺序无关紧要。
B. Beizer提出这5个必要条件的目的是为了使操作的执行完全依赖于条件的组合。其实对于某些不满足这几条的判定表,同样可以使用判定表设计测试用例,只不过还需要增加其它的测试用例。
6.优缺点
- 优点:它能把复杂的问题按各种可能的情况一一列举出来,简明而易于理解,也可以避免遗漏。
- 缺点:不能表达重复执行的动作,例如循环结构。
7.实战演练
需求描述:”……对功率大于50马力的机器、维修记录不全或已运行10年以上的机器,应给予优先的维修处理……” 。这里假定,“维修记录不全”和“优先维修处理”均已在别处有更严格的定义 。请建立判定表。
(1)确定规则的个数。规则个数的取值为2的n次方,n为条件个数。需求描述中有3个条件(功率大于50马力、维修记录不全、运行10年以上),每个条件有两个取值,故应有2的3次方,共8种规则;
(2)列出所有的条件桩和动作桩;

(3)填入条件项。可以从第1列开始次序减去1。按照二进制计算方法。如7(111)、6(110)、...、0(000);
(4)填入动作桩和动作顶,这样便得到如下图的初始判定表;
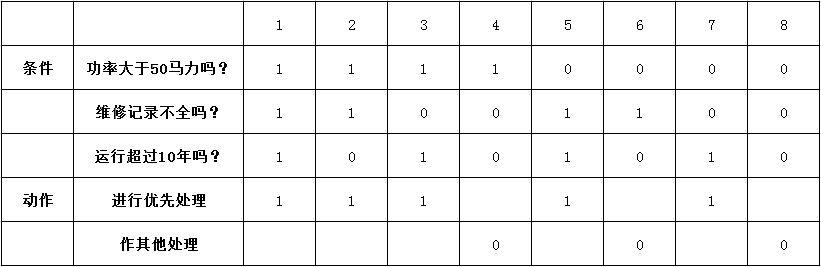
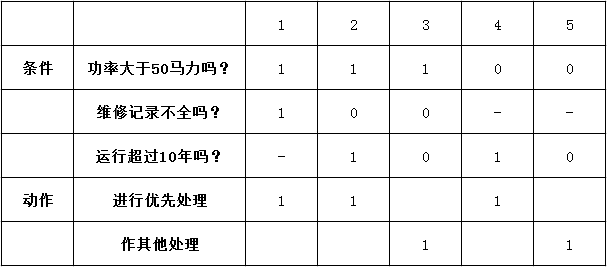
(5)化简,合并相似规则后得到如下图。
------------------------End------------------------