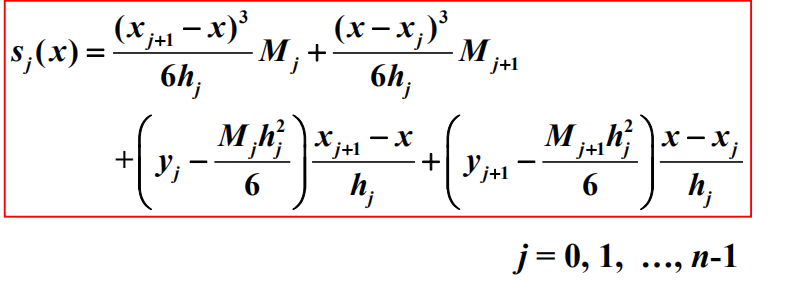分析:
第一问,给出的是第一类边界条件
第二问,给出的是第二类边界条件
我们按照想要的步骤,分别求第一类与第二类边界条件下的三次样条插值函数即可
为了不重复计算,且易于扩展,我们用C++编程,循环实现即可。
(这肯定不能手算的,手算必手酸)
1 #include <cstdio> 2 #include <iostream> 3 4 using namespace std; 5 6 const int N = 5; 7 8 int main() 9 { 10 // 录入数据 11 double x[N]={0.25,0.30,0.39,0.45,0.53}; 12 double y[N]={0.5,0.5477,0.6245,0.6708,0.7280}; 13 // 输出数据 14 printf("X(i),i=0...%d ",N-1); 15 for(int i=0;i<N;++i) 16 { 17 printf("%f ",x[i]); 18 } 19 printf(" Y(i),i=0...%d ",N-1); 20 for(int i=0;i<N;++i) 21 { 22 printf("%f ",y[i]); 23 } 24 printf(" "); 25 26 // 计算h[i] 27 double h[N]; 28 for(int i=0;i<N-1;++i) 29 { 30 h[i]=x[i+1]-x[i]; 31 } 32 // 输出数据 33 printf("h(i),i=0...%d ",N-2); 34 for(int i=0;i<N-1;++i) 35 { 36 printf("%f ",h[i]); 37 } 38 putchar(' '); 39 putchar(' '); 40 41 // 计算u[i],r[i] 42 double u[N],r[N]; 43 for(int i=1;i<N;++i) 44 { 45 u[i]=h[i-1]/(h[i-1] + h[i]); 46 r[i]=h[i]/(h[i-1] + h[i]); 47 } 48 // 输出数据 49 printf("u(i),i=1...%d ",N-1); 50 for(int i=1;i<N;++i) 51 { 52 printf("%f ",u[i]); 53 } 54 putchar(' '); 55 putchar(' '); 56 printf("r(i),i=1...%d ",N-1); 57 for(int i=1;i<N;++i) 58 { 59 printf("%f ",r[i]); 60 } 61 putchar(' '); 62 putchar(' '); 63 64 // 计算f[x(i-1),x(i)] 65 // 用f[i]表示f[x(i-1),x(i)] 66 double f[N+1]; 67 for(int i=1;i<N;++i) 68 { 69 f[i]=(y[i] - y[i-1])/(x[i] - x[i-1]); 70 } 71 // 输出数据 72 printf("f[x(i),x(i-1)],i=1...%d ",N-1); 73 for(int i=1;i<N;++i) 74 { 75 printf("%f ",f[i]); 76 } 77 putchar(' '); 78 putchar(' '); 79 80 // 记录两个导数 81 f[0]=1; 82 f[N]=0.6868; 83 84 // 计算d(i) 85 double d[N+1]; 86 d[0]=6*(f[1]-f[0])/h[0]; 87 for(int i=1;i<N-1;++i) 88 { 89 d[i]=6*(f[i+1]-f[i])/(h[i-1] + h[i]); 90 } 91 d[N]=6*(f[N]-f[N-1])/h[N-2]; 92 93 printf("d[i],i=0...%d ",N); 94 for(int i=0;i<=N;++i) 95 { 96 printf("%f ",d[i]); 97 } 98 99 // AX=B 100 // X=[A^(-1)]*B 101 return 0; 102 }

求出上述数据后,代入矩阵求解即可得到所有的M( i ) 的值,对应矩阵的求逆与矩阵乘法的操作,用python或matlab都可以实现,这里不再重复实现,只需将上述计算所得的数据,写入相应的文件,然后在python中读取调用numpy库函数或用matlab实现都可。

所有数据都已经求出后,带入,三次样条函数即为所求
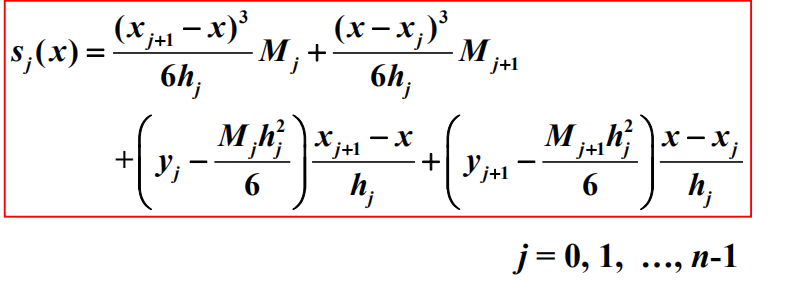
第二问给出了第二类边界条件
M0与Mn即为给出的第二类边界条件的值,这里都是0,计算更加的简单,等式右边的直接与之前一问所求的d相同,无需重复计算
同样带入如下矩阵,
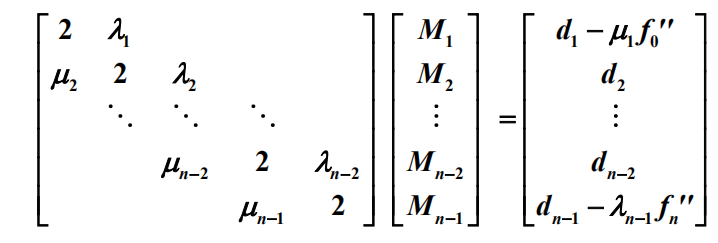
利用矩阵的逆运算,即可求出剩余的M1,...,n-1.
同样,所有数据已知,带入,三次样条函数即为所求。