| 这个作业属于哪个班级 | 数据结构--网络2011/2012 | |
|---|---|---|
| 这个作业的目标 | 学习数据结构基本概念、时间复杂度、顺序表、单链表、有序表的结构设计及运算操作 | |
| 姓名 | 郑俊佳 |
目录:
1.1 绪论
1.1.1 数据结构有哪些结构,各种结构解决什么问题?
1.1.2 时间复杂度及空间复杂度概念。
1.1.3 时间复杂度有哪些?如何计算程序的时间复杂度和空间复杂度
1.2 线性表
1.2.1 顺序表
1.2.2 链表
1.2.3 有序表
2.PTA实验作业
2.1 两个有序序列的中位数
2.2 一元多项式的乘法与加法运算
3.阅读代码
3.1 题目及解题代码
0.PTA得分截图

1.本周学习总结(5分)
请回答下面每个知识点问题,并详细介绍相关知识点内容。
1.1 绪论(1分)
1.1.1 数据结构有哪些结构,各种结构解决什么问题?
- 数据结构分为逻辑结构&储存结构;
- 逻辑结构:数据元素之间的逻辑关系,体现在文字描述;
- 储存结构:将逻辑结构转化成计算机能够储存的结构,体现在代码设计;
1.1.2 时间复杂度及空间复杂度概念。
时间复杂度&空间复杂度统称为算法复杂度;
时间复杂度指执行这个算法所需要的计算工作量;
空间复杂度指执行这个算法所需要的内存空间;
空间复杂度:
1:空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度;
2:一个算法在计算机上占用的内存包括:程序代码所占用的空间,输入输出数据所占用的空间,辅助变量所占用的空间这三个方面,程序代码所占用的空间取决于算法本身的长短,输入输出数据所占用的空间取决于要解决的问题,是通过参数表调用函数传递而来,只有辅助变量是算法运行过程中临时占用的存储空间,与空间复杂度相关;
3:通常来说,只要算法不涉及到动态分配的空间,以及递归、栈所需的空间,空间复杂度通常为0(1);
4: 对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时,可能会使空间复杂度的性能变差,即可能导致占用较多的存储空间;反之,求一个较好的空间复杂度时,可能会使时间复杂度的性能变差,即可能导致占用较长的运行时间。另外,算法的所有性能之间都存在着或多或少的相互影响。因此,当设计一个算法(特别是大型算法)时,要综合考虑算法的各项性能,算法的使用频率,算法处理的数据量的大小,算法描述语言的特性,算法运行的机器系统环境等各方面因素,才能够设计出比较好的算法。
1.1.3 时间复杂度有哪些?如何计算程序的时间复杂度和空间复杂度,举例说明。
常见的时间复杂度有:
- 常数阶O(1),
- 对数阶O(log2 n),
- 线性阶O(n),
- 线性对数阶O(n log2 n),
- 平方阶O(n^2),
- 立方阶O(n^3)
- k次方阶O(n^K),
- 指数阶O(2^n)。
随着n的不断增大,时间复杂度不断增大,算法花费时间越多。
计算时间复杂度法子:
(1).对于一些简单的输入输出语句或赋值语句,近似认为需要O(1)时间
(2).对于顺序结构,需要依次执行一系列语句所用的时间可采用大O下"求和法则" 求和法则:
是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1(n)+T2(n)=O(max(f(n),g(n)))。
特别地,若T1(m)=O(f(m)), T2(n)=O(g(n)),则 T1(m)+T2(n)=O(f(m)+g(n))
(3).对于选择结构,如if语句,它的主要时间耗费是在执行then字句或else字句所用的时间,需注意的是检验条件也需要O(1)时间
(4).对于循环结构,循环语句的运行时间主要体现在多次迭代中执行循环体以及检验循环条件的时间耗费,一般可用大O下"乘法法则":
是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1T2=O(f(n)g(n))
(5).对于复杂的算法,可以将它分成几个容易估算的部分,然后利用求和法则和乘法法则技术整个算法的时间复杂度
另外还有以下2个运算法则:(1) 若g(n)=O(f(n)),则O(f(n))+O(g(n))=O(f(n));(2)O(Cf(n)) = O(f(n)),其中C是一个正常数。
如果算法中包含嵌套的循环,则基本语句通常是最内层的循环体,如果算法中包含并列的循环,则将并列循环的时间复杂度相加。
例如:
for (i=1; i<=n; i++)
x++;
for (i=1; i<=n; i++)
{
for (j=1; j<=n; j++)
x++;
}
第一个for循环的时间复杂度为O(n),第二个for循环的时间复杂度为O(n2),则整个算法的时间复杂度为O(n+n2)=O(n2)。
1.2 线性表(1分)
1.2.1 顺序表
顺序表结构体定义:
typedef struct {
Elemtype data[MaxSize];//存放顺序表元素
int length;//存放顺序表长度
}List;
typedef List* SqList;
顺序表创建操作:
void CreateList(SqList &L,int n)
{
int i;
L=new List;
L->length=n;
for(i=0;i<L->length;i++)
cin>>L->data[i];
}
顺序表插入操作:
void InsertSq(SqList& L, int x)
{
int i;
for (i = 0; i < L->length; i++)
{
if (L->data[i] > x)
break;
}
int j;
for (j = L->length;j > i;j--)
L->data[j] = L->data[j - 1];
L->data[i] = x;
L->length++;
}
顺序表删除操作:
(1)删除区间数:
void DelNode(SqList& L, int min, int max)
{
int k = 0,i;
for (i = 0; i < L->length; i++)
{
if (!(L->data[i] >= min && L->data[i] <= max))
{
L->data[k] = L->data[i];
k++;
}
}
L->length = k;
}
(2)删除特定位置:
bool ListDelete(SqList &L,int i)
{
if(i<1||i>L->length)
return false;
i--;
int j;
for(j=i;j<L->length-1 ;j++)
L->data[j]=L->data[j+1];
L->length--;
return ture;
}
假设Pi是在第i个元素之前插入一个元素的概率,则在长度为n的线性表中插入一个元素时所需移动元素次数的期望值(平均次数)为:
1.
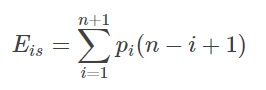
假设qi是删除第i个元素的概率,则在长度为n的线性表中删除一个元素时所需移动元素次数的期望值(平均次数)为:
2.
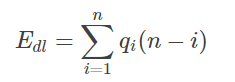
假定在线性表上的任意位置上插入或删除元素都是等概率的,即:
3.

通过3我们可以将上面的1和2进行相应的简化,其简化结果为:
4.
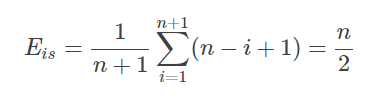

1.2.2 链表(2分)
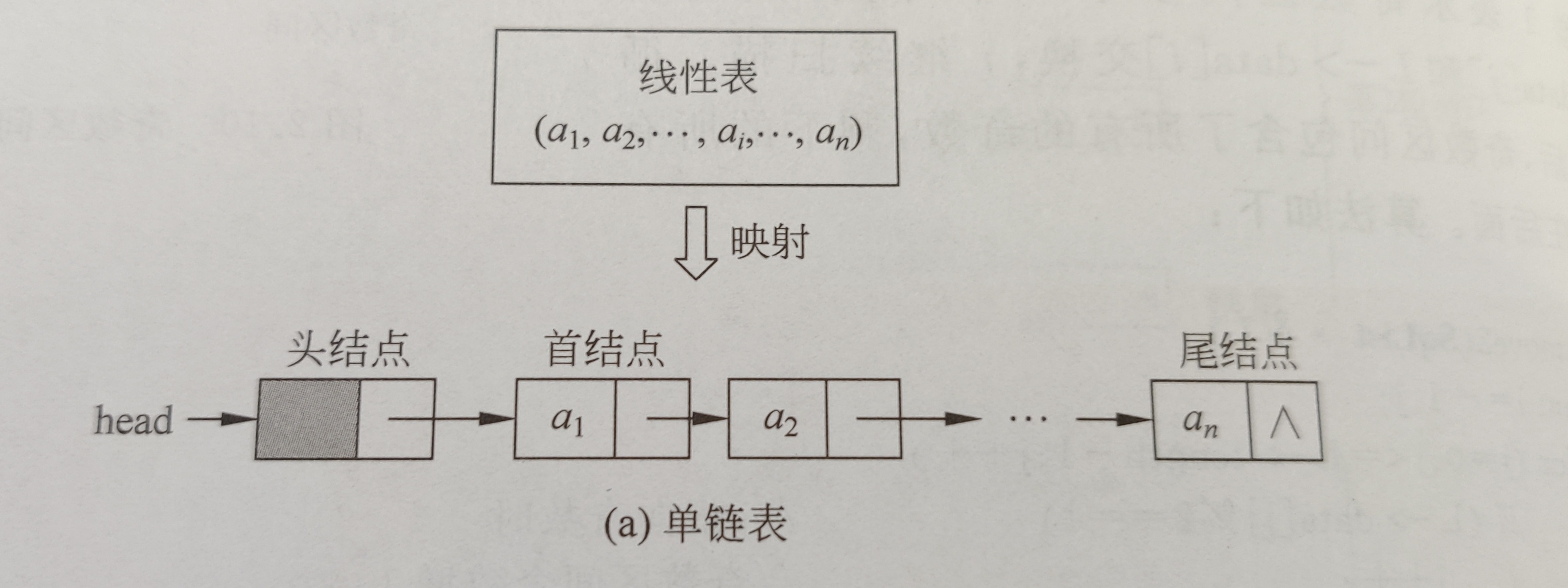
LinkNode类型声明:
typedef struct LNode
{ ElemType data;//用于储存元素值
struct LNode * next;//指向后继结点
}LinkNode;//单链表结点类型
ElemType自定义类型声明:
typedef int ElemType;
头插法代码:
void CreateListF(LinkNode * &L,ElemType a[],int n)
{ LinkNode * s;
L=(LinkNode *)malloc(sizeof(LinkNode));
L->next=NULL; //创建头结点,其next域置为NULL
for(int i=0;i<n;i++) //循环建立数据结点s
{ s=(LinkNode *)malloc(sizeof(LinkNode));
s->data=a[i]; //创建数据结点s
s->next=L->next; //将结点s插入到原首节点之前,头节点之后
L->next=s;
}
}
尾插法代码:
void CreateListR(LinkNode * &L,ElemType a[],int n)
{ LinkNode * s,* r;
L=(LinkNode *)malloc(sizeof(LinkNode)); //创建头结点
r=L; //r始终指向尾结点,初始时指向头结点
for(int i=0;i<n;i++) //循环建立数据结点
{ s=(LinkNode *)malloc(sizeof(LinkNode));
s->data=a[i]; //创建数据结点s
r->next=s; //将结点s插入到结点r之后
r=s;
}
r->next=NULL; //尾结点的next域置为NULL
}
链表插入代码:
bool LinkInsert(LinkNode*& L, int i, ElemType e)
{
int j = 0;
LinkNode* p = L, * s; //p指向头结点,j置为0(即头结点的序号为0)
if (i <= 0) //i错误返回false
return false;
while (j < i - 1 && p != NULL) //查找第i-1个结点p
{
j++;
p = p->next;
}
if (p == NULL) //未找到第i-1个结点,返回false
return false;
else //找到第i-1个结点p,插入新结点并返回true
{
s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = e; //创建新结点s,其data域置为e
s->next = p->next; //将结点s插入到结点p之后
p->next = s;
return true;
}
}
链表删除代码:
bool ListDelete(LinkNode*& L, int i, ElemType& e)
{
int j = 0;
LinkNode* p = L, * q; //p指向头结点,j置为0(即头结点的序号为0)
if (i <= 0) //i错误返回false
return false;
while (j < i - 1 && p != NULL) //查找第i-1个结点
{
j++;
p = p->next;
}
if (p == NULL) //未找到第i-1个结点,返回false
return false;
else //找到第i-1个结点p
{
q = p->next; //q指向第i个结点
if (q == NULL) //若不存在第i个结点,返回false
return false;
e = q->data;
p->nxet = q->next; //从单链表中删除q结点
free(q); //释放q结点
return true; //返回true表示成功删除第i个结点
}
}
重构链表如何操作?链表操作注意事项请罗列。
链表及顺序表在存储空间、插入及删除操作方面区别,优势?
1.2.3 有序表(1分)
有序顺序表插入操作,代码或伪代码介绍。
有序顺序表插入代码:
void ListInsert(SqList * &L,ElemType e)
{
int i=0,j;
while(i<L->length&&L->data[i]<e)
i++; //查找值为e的元素
for(j=ListLength(L);j>i;j--) //将data[i]及后面的元素后移一个位置
L->data[j]=L->data[j-1];
L->data[i]=e;
L->length++; //有序顺序表的长度加一
}
有序单链表数据插入、删除。代码或伪代码介绍。
有序单链表数据插入代码:
void ListInsert(LinkNode *&L,ElemType e)
{
LinkInsert *pre=L,*p;
while(pre->next!=NULL&&pre->next->data<e)
pre=pre->next; //找到插入结点的前驱结点pre
p=new LinkNode;
p->data=e; //创建存放e的数据结点p
p->next=pre->next; //在pre结点之后插入p结点
pre->next=p;
}
有序链表合并,代码或伪代码。尽量结合图形介绍。
void MergeList(LinkList& L1, LinkList L2)
{
LinkList p;
LinkList q;
p = new LNode;
p = L1->next;
q = new LNode;
q = L2->next;
L1->next = NULL;
LinkList tail;
tail = L1;
while (p && q)
{
if (p->data < q->data)
{
tail->next = p;
tail=p;
p=p->next;
}
else if (p->data > q->data)
{
tail->next = q;
tail=q;
q=q->next;
}
else
{
tail->next = p;
p = p->next;
q = q->next;
tail = tail->next;
}
}
if (p == NULL)
{
tail->next = q;
}
else
{
tail->next = p;
}
}
有序链表合并和有序顺序表合并,有哪些优势?
2.PTA实验作业(4分)
此处请放置下面2题代码所在码云地址(markdown插入代码所在的链接)。如何上传VS代码到码云
2.1 两个有序序列的中位数
2.1.1 解题思路及伪代码
#include <iostream>
#define MaxSize 100001
using namespace std;
typedef int ElemType;
typedef struct {
ElemType data[MaxSize];
int length;
}List;
typedef List* SqList;
int main()
{
int N;
cin >> N;
int i;
SqList L1, L2, L;
L1 = new List;
L2 = new List;
L1->length = 0;
L2->length = 0;
L = new List;
L->length = 0;
for (i = 0; i < N; i++)
{
cin >> L1->data[i];
}
for (i = 0; i < N; i++)
{
cin >> L2->data[i];
}
int j ;
int k ;
for(j=0,k=0;j<N&&k<N;)
{
if (L1->data[j] < L2->data[k])
{
L->data[L->length] = L1->data[j];
j++;
}
else
{
L->data[L->length] = L2->data[k];
k++;
}
L->length++;
}
if (j < N)
{
for (j; j < N; j++)
{
L->data[L->length] = L1->data[j];
L->length++;
}
}
if (k < N)
{
for (k;k< N; k++)
{
L->data[L->length] = L2->data[k];
L->length++;
}
}
cout << (L->data[N] + L->data[N - 1]) / 2;
}
2.1.2 碰到问题及解决方法
无法合并统一,寻找中位数是会超时等。
2.2 一元多项式的乘法与加法运算
2.2.1 解题思路及伪代码
2.2.2 碰到问题及解决方法
3.阅读代码(1分)
找1份优秀代码,理解代码功能,并讲出你所选代码优点及可以学习地方。主要找以下类型代码:
考研题种关于线性表内容。可以找参加过考研的学长学姐拿。尤其是想要考研同学,可以结合本章内容,用考研题训练学习。
ACM题解
leecode面试刷题网站,找线性表相关题目阅读分析。
leecode经典题目
注意:不能选教师布置在PTA的题目。完成内容如下。
3.1 题目及解题代码
可截图,或复制代码,需要用代码符号渲染。
3.2 该题的设计思路及伪代码
链表题目,请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。