自动编码器是一种特殊的神经网络,经过训练可以将其输入复制到其输出。例如,给定手写数字的图像,自动编码器首先将图像编码为较低维的潜在表示,然后将潜在表示解码回图像。自动编码器学会在最小化重构误差的同时压缩数据。
要了解有关自动编码器的更多信息,请考虑阅读Ian Goodfellow,Yoshua Bengio和Aaron Courville撰写的Deep Learning中的第14章。
导入TensorFlow和其他库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.metrics import accuracy_score, precision_score, recall_score
from sklearn.model_selection import train_test_split
from tensorflow.keras import layers, losses
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Model
加载数据集
首先,您将使用Fashon MNIST数据集训练基本的自动编码器。该数据集中的每个图像均为28x28像素。
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print (x_train.shape)
print (x_test.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 32768/29515 [=================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26427392/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 8192/5148 [===============================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4423680/4422102 [==============================] - 0s 0us/step (60000, 28, 28) (10000, 28, 28)
第一个示例:基本自动编码器
定义一个具有两个密集层的自动encoder :一个encoder (将图像压缩为64维潜矢量)和一个decoder (从decoder空间重建原始图像)。
要定义模型,请使用Keras模型子类API 。
latent_dim = 64
class Autoencoder(Model):
def __init__(self, encoding_dim):
super(Autoencoder, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential([
layers.Flatten(),
layers.Dense(latent_dim, activation='relu'),
])
self.decoder = tf.keras.Sequential([
layers.Dense(784, activation='sigmoid'),
layers.Reshape((28, 28))
])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Autoencoder(latent_dim)
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
使用x_train作为输入和目标来训练模型。 encoder将学习将数据集从784个维压缩到潜在空间,而decoder将学习重建原始图像。 。
autoencoder.fit(x_train, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test, x_test))
Epoch 1/10 1875/1875 [==============================] - 3s 1ms/step - loss: 0.0236 - val_loss: 0.0133 Epoch 2/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0116 - val_loss: 0.0106 Epoch 3/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0100 - val_loss: 0.0097 Epoch 4/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0094 - val_loss: 0.0094 Epoch 5/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0091 - val_loss: 0.0091 Epoch 6/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0090 - val_loss: 0.0091 Epoch 7/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0089 - val_loss: 0.0089 Epoch 8/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0088 - val_loss: 0.0089 Epoch 9/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0088 - val_loss: 0.0088 Epoch 10/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.0087 - val_loss: 0.0088 <tensorflow.python.keras.callbacks.History at 0x7f7076d484e0>
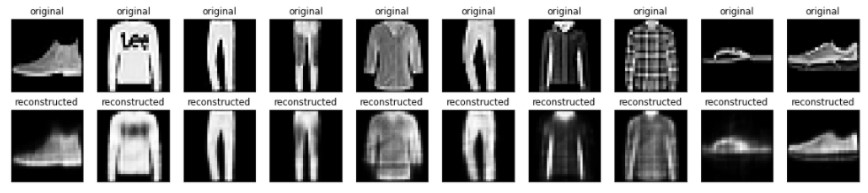
现在已经对模型进行了训练,让我们通过对测试集中的图像进行编码和解码来对其进行测试。
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i])
plt.title("original")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i])
plt.title("reconstructed")
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

第二个例子:图像去噪

还可以训练自动编码器以消除图像中的噪点。在以下部分中,您将通过对每个图像应用随机噪声来创建Fashion MNIST数据集的嘈杂版本。然后,您将使用嘈杂的图像作为输入,并以原始图像为目标来训练自动编码器。
让我们重新导入数据集以省略之前所做的修改。
(x_train, _), (x_test, _) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train[..., tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape)
(60000, 28, 28, 1)
给图像添加随机噪声
noise_factor = 0.2
x_train_noisy = x_train + noise_factor * tf.random.normal(shape=x_train.shape)
x_test_noisy = x_test + noise_factor * tf.random.normal(shape=x_test.shape)
x_train_noisy = tf.clip_by_value(x_train_noisy, clip_value_min=0., clip_value_max=1.)
x_test_noisy = tf.clip_by_value(x_test_noisy, clip_value_min=0., clip_value_max=1.)
绘制嘈杂的图像。
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
plt.show()

定义卷积自动编码器
在本例中,将训练使用卷积自动编码Conv2D层在encoder ,和Conv2DTranspose层在decoder 。
class Denoise(Model):
def __init__(self):
super(Denoise, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Input(shape=(28, 28, 1)),
layers.Conv2D(16, (3,3), activation='relu', padding='same', strides=2),
layers.Conv2D(8, (3,3), activation='relu', padding='same', strides=2)])
self.decoder = tf.keras.Sequential([
layers.Conv2DTranspose(8, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2DTranspose(16, kernel_size=3, strides=2, activation='relu', padding='same'),
layers.Conv2D(1, kernel_size=(3,3), activation='sigmoid', padding='same')])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = Denoise()
autoencoder.compile(optimizer='adam', loss=losses.MeanSquaredError())
autoencoder.fit(x_train_noisy, x_train,
epochs=10,
shuffle=True,
validation_data=(x_test_noisy, x_test))
Epoch 1/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0177 - val_loss: 0.0108 Epoch 2/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0100 - val_loss: 0.0095 Epoch 3/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0091 - val_loss: 0.0087 Epoch 4/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0085 - val_loss: 0.0084 Epoch 5/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0082 - val_loss: 0.0083 Epoch 6/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0080 - val_loss: 0.0080 Epoch 7/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0079 - val_loss: 0.0079 Epoch 8/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0078 - val_loss: 0.0078 Epoch 9/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0077 - val_loss: 0.0077 Epoch 10/10 1875/1875 [==============================] - 4s 2ms/step - loss: 0.0076 - val_loss: 0.0076 <tensorflow.python.keras.callbacks.History at 0x7f70600ede48>
让我们看一下编码器的摘要。请注意,图像是如何从28x28下采样到7x7的。
autoencoder.encoder.summary()
Model: "sequential_2" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d (Conv2D) (None, 14, 14, 16) 160 _________________________________________________________________ conv2d_1 (Conv2D) (None, 7, 7, 8) 1160 ================================================================= Total params: 1,320 Trainable params: 1,320 Non-trainable params: 0 _________________________________________________________________
解码器将图像从7x7升采样到28x28。
autoencoder.decoder.summary()
Model: "sequential_3" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_transpose (Conv2DTran (None, 14, 14, 8) 584 _________________________________________________________________ conv2d_transpose_1 (Conv2DTr (None, 28, 28, 16) 1168 _________________________________________________________________ conv2d_2 (Conv2D) (None, 28, 28, 1) 145 ================================================================= Total params: 1,897 Trainable params: 1,897 Non-trainable params: 0 _________________________________________________________________
绘制由自动编码器产生的噪声图像和去噪图像。
encoded_imgs = autoencoder.encoder(x_test).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# display original + noise
ax = plt.subplot(2, n, i + 1)
plt.title("original + noise")
plt.imshow(tf.squeeze(x_test_noisy[i]))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# display reconstruction
bx = plt.subplot(2, n, i + n + 1)
plt.title("reconstructed")
plt.imshow(tf.squeeze(decoded_imgs[i]))
plt.gray()
bx.get_xaxis().set_visible(False)
bx.get_yaxis().set_visible(False)
plt.show()

第三个示例:异常检测总览
在此示例中,您将训练自动编码器以检测ECG5000数据集上的异常。该数据集包含5,000个心电图 ,每个心电图包含140个数据点。您将使用数据集的简化版本,其中每个示例都被标记为0 (对应于异常节奏)或1 (对应于正常节奏)。您对识别异常节律感兴趣。
您将如何使用自动编码器检测异常?回想一下,对自动编码器进行了培训,以最大程度地减少重构误差。您将只按照正常节奏训练自动编码器,然后使用它来重构所有数据。我们的假设是,异常节律将具有较高的重建误差。然后,如果重构误差超过固定阈值,则将节奏分类为异常。
加载心电图数据
您将使用的数据集基于timeseriesclassification.com中的数据集。
# Download the dataset
dataframe = pd.read_csv('http://storage.googleapis.com/download.tensorflow.org/data/ecg.csv', header=None)
raw_data = dataframe.values
dataframe.head()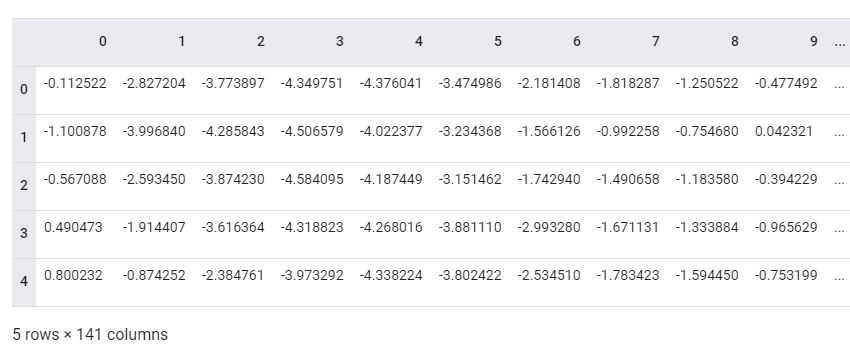
# The last element contains the labels
labels = raw_data[:, -1]
# The other data points are the electrocadriogram data
data = raw_data[:, 0:-1]
train_data, test_data, train_labels, test_labels = train_test_split(
data, labels, test_size=0.2, random_state=21
)
将数据标准化为[0,1] 。
min_val = tf.reduce_min(train_data)
max_val = tf.reduce_max(train_data)
train_data = (train_data - min_val) / (max_val - min_val)
test_data = (test_data - min_val) / (max_val - min_val)
train_data = tf.cast(train_data, tf.float32)
test_data = tf.cast(test_data, tf.float32)
您将仅使用正常节奏训练自动编码器,在此数据集中标记为1 。将正常节律与异常节律分开。
train_labels = train_labels.astype(bool)
test_labels = test_labels.astype(bool)
normal_train_data = train_data[train_labels]
normal_test_data = test_data[test_labels]
anomalous_train_data = train_data[~train_labels]
anomalous_test_data = test_data[~test_labels]
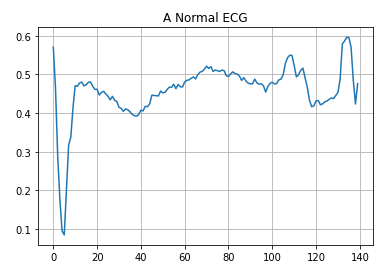
绘制正常的心电图。
plt.grid()
plt.plot(np.arange(140), normal_train_data[0])
plt.title("A Normal ECG")
plt.show()
绘制异常的心电图。
plt.grid()
plt.plot(np.arange(140), anomalous_train_data[0])
plt.title("An Anomalous ECG")
plt.show()

建立模型
class AnomalyDetector(Model):
def __init__(self):
super(AnomalyDetector, self).__init__()
self.encoder = tf.keras.Sequential([
layers.Dense(32, activation="relu"),
layers.Dense(16, activation="relu"),
layers.Dense(8, activation="relu")])
self.decoder = tf.keras.Sequential([
layers.Dense(16, activation="relu"),
layers.Dense(32, activation="relu"),
layers.Dense(140, activation="sigmoid")])
def call(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return decoded
autoencoder = AnomalyDetector()
autoencoder.compile(optimizer='adam', loss='mae')
请注意,仅使用常规ECG训练自动编码器,但使用完整的测试集对其进行评估。
history = autoencoder.fit(normal_train_data, normal_train_data,
epochs=20,
batch_size=512,
validation_data=(test_data, test_data),
shuffle=True)
Epoch 1/20 5/5 [==============================] - 0s 47ms/step - loss: 0.0589 - val_loss: 0.0535 Epoch 2/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0561 - val_loss: 0.0519 Epoch 3/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0536 - val_loss: 0.0502 Epoch 4/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0499 - val_loss: 0.0483 Epoch 5/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0457 - val_loss: 0.0465 Epoch 6/20 5/5 [==============================] - 0s 6ms/step - loss: 0.0417 - val_loss: 0.0437 Epoch 7/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0378 - val_loss: 0.0418 Epoch 8/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0343 - val_loss: 0.0403 Epoch 9/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0312 - val_loss: 0.0386 Epoch 10/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0288 - val_loss: 0.0377 Epoch 11/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0270 - val_loss: 0.0367 Epoch 12/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0257 - val_loss: 0.0363 Epoch 13/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0247 - val_loss: 0.0356 Epoch 14/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0239 - val_loss: 0.0355 Epoch 15/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0234 - val_loss: 0.0350 Epoch 16/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0230 - val_loss: 0.0348 Epoch 17/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0226 - val_loss: 0.0344 Epoch 18/20 5/5 [==============================] - 0s 4ms/step - loss: 0.0221 - val_loss: 0.0343 Epoch 19/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0218 - val_loss: 0.0340 Epoch 20/20 5/5 [==============================] - 0s 5ms/step - loss: 0.0214 - val_loss: 0.0338
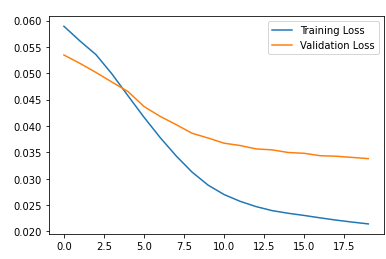
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
<matplotlib.legend.Legend at 0x7f7076948a20>
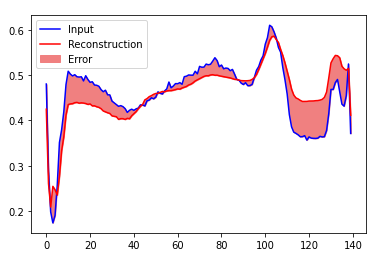
如果重建误差大于正常训练示例的一个标准偏差,您将很快将ECG归类为异常。首先,让我们从训练集中绘制正常的ECG,通过自动编码器进行编码和解码后的重构以及重构误差。
encoded_imgs = autoencoder.encoder(normal_test_data).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
plt.plot(normal_test_data[0],'b')
plt.plot(decoded_imgs[0],'r')
plt.fill_between(np.arange(140), decoded_imgs[0], normal_test_data[0], color='lightcoral' )
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
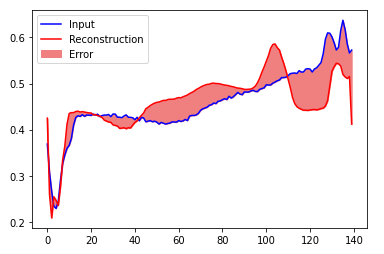
创建一个类似的图,这次是一个异常的测试示例。
encoded_imgs = autoencoder.encoder(anomalous_test_data).numpy()
decoded_imgs = autoencoder.decoder(encoded_imgs).numpy()
plt.plot(anomalous_test_data[0],'b')
plt.plot(decoded_imgs[0],'r')
plt.fill_between(np.arange(140), decoded_imgs[0], anomalous_test_data[0], color='lightcoral' )
plt.legend(labels=["Input", "Reconstruction", "Error"])
plt.show()
检测异常
通过计算重建损失是否大于固定阈值来检测异常。在本教程中,您将计算出训练集中正常样本的平均平均误差,如果重构误差大于训练集中的一个标准偏差,则将未来的样本归类为异常。
从训练集中绘制正常心电图上的重建误差
reconstructions = autoencoder.predict(normal_train_data)
train_loss = tf.keras.losses.mae(reconstructions, normal_train_data)
plt.hist(train_loss, bins=50)
plt.xlabel("Train loss")
plt.ylabel("No of examples")
plt.show()
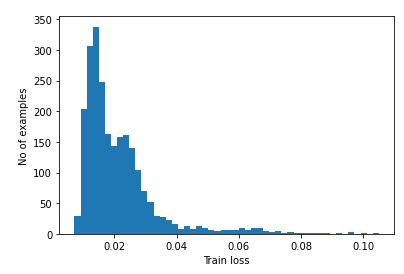
选择一个阈值,该阈值要比平均值高一个标准偏差。
threshold = np.mean(train_loss) + np.std(train_loss)
print("Threshold: ", threshold)
Threshold: 0.033656895
如果检查测试集中异常示例的重构误差,您会发现大多数重构误差都比阈值大。通过更改阈值,可以调整分类器的精度和召回率 。
reconstructions = autoencoder.predict(anomalous_test_data)
test_loss = tf.keras.losses.mae(reconstructions, anomalous_test_data)
plt.hist(test_loss, bins=50)
plt.xlabel("Test loss")
plt.ylabel("No of examples")
plt.show()

如果重建误差大于阈值,则将ECG归类为异常。
def predict(model, data, threshold):
reconstructions = model(data)
loss = tf.keras.losses.mae(reconstructions, data)
return tf.math.less(loss, threshold)
def print_stats(predictions, labels):
print("Accuracy = {}".format(accuracy_score(labels, preds)))
print("Precision = {}".format(precision_score(labels, preds)))
print("Recall = {}".format(recall_score(labels, preds)))
preds = predict(autoencoder, test_data, threshold)
print_stats(preds, test_labels)
Accuracy = 0.943 Precision = 0.9921722113502935 Recall = 0.9053571428571429