// 此博文为迁移而来,写于2015年5月16日,不代表本人现在的观点与看法。原始地址:http://blog.sina.com.cn/s/blog_6022c4720102w0d8.html
UPDATE(20180818):移步新的网络流系列╮(╯▽╰)╭。
I、网络流基础
II、网络流进阶之转换对偶图
III、网络流进阶之费用流
1、前言
先来说一个概念——最小割。最小割是什么呢?在网络流上,截去最小的流,使源点到汇点没有流量可以流通。仔细想想,其实就是最大能通过的流量。于是就能得到一个定理——最小割=最大流。
今天所讲的一种模型,是将平面图转换为对偶图,用最短路来求最小割。它的速度比起裸最小割(Dinic)更快(但是仅适用于网格图)。先来看一道例题:
狼抓兔子 [ BZOJ 1001 / Beijing 2006 ]
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:

左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4)。有以下三种类型的道路 1:(x,y)<==>(x+1,y) 2:(x,y)<==>(x,y+1) 3:(x,y)<==>(x+1,y+1) 道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下解(N,M)的窝中去,狼王开始伏击这些兔子.当然为了保险起见,如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼,才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦.
输入格式
第一行为N,M.表示网格的大小,N,M均小于等于1000.接下来分三部分第一部分共N行,每行M-1个数,表示横向道路的权值. 第二部分共N-1行,每行M个数,表示纵向道路的权值. 第三部分共N-1行,每行M-1个数,表示斜向道路的权值. 输入文件保证不超过10M
输出格式
输出一个整数,表示参与伏击的狼的最小数量.
输入样例
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
输出样例
14
2、转换
其实这道题,直接用Dinic跑最大流,是不会WA的,但是数据之大让Dinic无能为力。我们注意到,我们在割掉一条边的时候(即派遣狼)在边上画一条杠,而最小割就是用最小的代价画一坨杠让图不连通。我们可以把我们画的杠看作一条联通这条边两侧方块(如果在网格图中)的边,而且你会发现,要使起点和终点不连通,我们就会画出一串可以相连的杠(可以试一试),所以这种在平面图上求最小割的方法就应运而生了。
所以,这种方法的本质就是在这一串的割线上跑最短路。
那么,我们这个时候构建一个对偶图:对于每一条边,必定会有两个面在其左右侧。则我们将左右侧两个面连一条边,且其权值为原来那条边的权值。即对于下图中的一条权值为5的边,在对偶图中对应的就是一条由1连向2的权值为5的边。
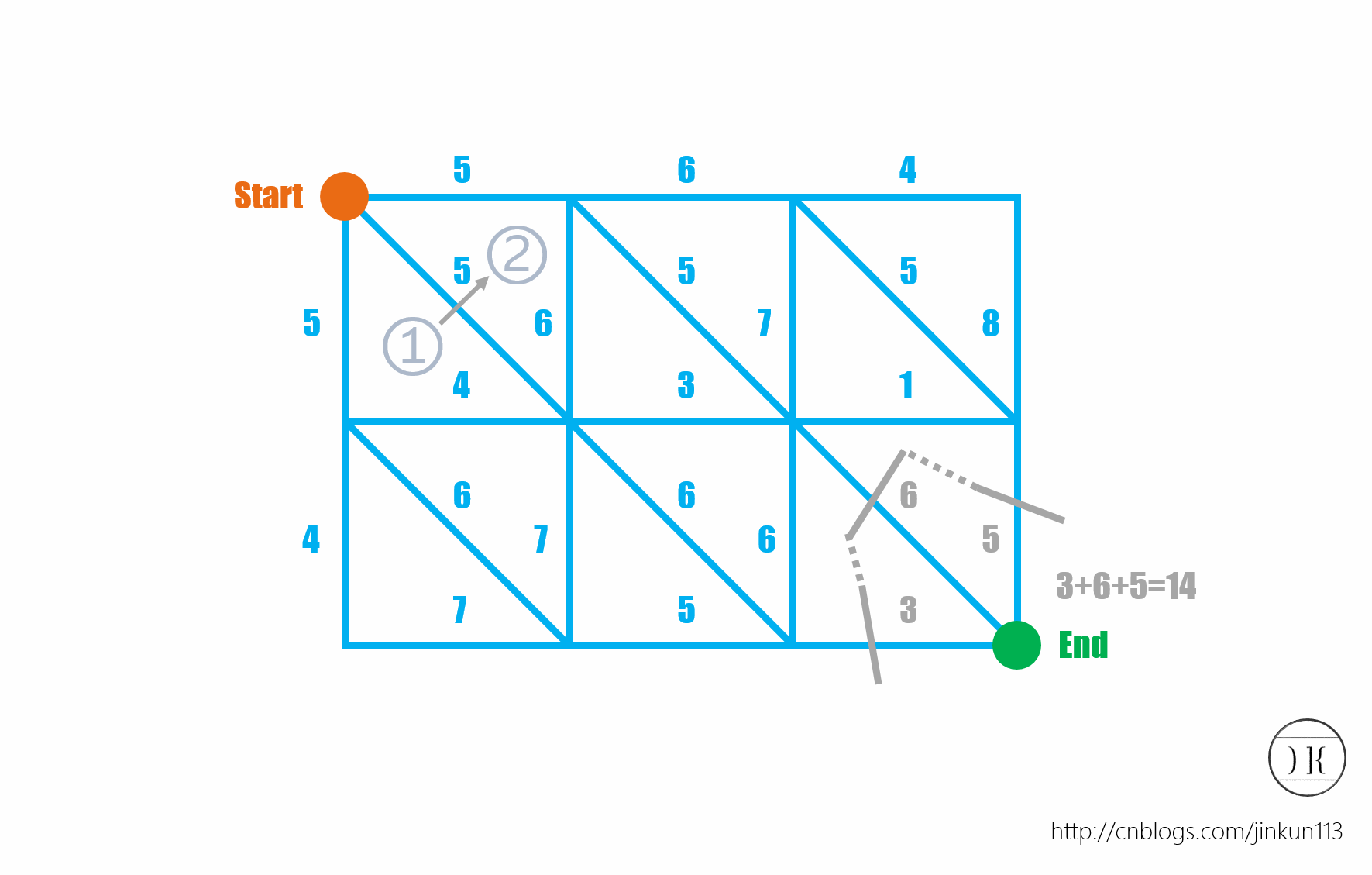

Code:(P.S. 我的代码构建对偶图的方式比较鬼,尽管是对的。。大家可以自行脑补更好的方法 = =)
-----------------------------------------------------------------------------------------------------
#include<cstdio>
#include<cstring>
#include<queue>
#include<cstdlib>
#define MAXN 1000005
#define INF 0x3f3f3f3f
using namespace std;
struct Edge
{
int v,next,val;
};
Edge edge[6*MAXN];
int ggd=INF;
int cycle,n,m,x,now,h[MAXN*6],s,t,dist[MAXN*6],vis[MAXN*6];
void addEdge(int u,int v,int val)
{
now++;
edge[now].v=v;
edge[now].next=h[u];
edge[now].val=val;
h[u]=now;
}
void init1()
{
for (int i=1;i<=n;i++)
for (int j=1;j<=m-1;j++)
{
scanf("%d",&x),ggd=min(ggd,x);
if (i==1) { addEdge(t,(i-1)*cycle+j*2,x); addEdge((i-1)*cycle+j*2,t,x); }
else if (i==n) { addEdge((i-2)*cycle+j*2-1,s,x); addEdge(s,(i-2)*cycle+j*2-1,x); }
else { addEdge((i-2)*cycle+j*2-1,(i-1)*cycle+j*2,x); addEdge((i-1)*cycle+j*2,(i-2)*cycle+j*2-1,x); }
}
}
void init2()
{
for (int i=1;i<=n-1;i++)
for (int j=1;j<=m;j++)
{
scanf("%d",&x),ggd=min(ggd,x);
if (j==1) { addEdge(s,(i-1)*cycle+1,x); addEdge((i-1)*cycle+1,s,x); }
else if (j==m) { addEdge(i*cycle,t,x); addEdge(t,i*cycle,x); }
else { addEdge((i-1)*cycle+j*2-2,(i-1)*cycle+j*2-1,x); addEdge((i-1)*cycle+j*2-1,(i-1)*cycle+j*2-2,x); }
}
}
void init3()
{
int tot=-1;
for (int i=1;i<=n-1;i++)
for (int j=1;j<=m-1;j++)
{
scanf("%d",&x); tot+=2,ggd=min(ggd,x);
addEdge(tot,tot+1,x); addEdge(tot+1,tot,x);
}
}
void init()
{
scanf("%d %d",&n,&m);
cycle=(m-1)*2;
s=(n-1)*(m-1)*2+1,t=s+1;
init1();
init2();
init3();
if(n==1||m==1){ printf("%d",ggd); exit(0); }
}
struct state
{
int num,nowVal;
state() {}
state(int _num,int _nowVal):num(_num),nowVal(_nowVal) {}
friend bool operator < (state a,state b) { return a.nowVal>b.nowVal; }
};
priority_queue q;
int Dijkstra()
{
memset(dist,INF,sizeof(dist));
q.push(state(s,0));
dist[s]=0,vis[s]=0;
while (q.size())
{
state temp=q.top(); q.pop();
if (temp.nowVal>dist[temp.num]) continue;
if (temp.num==t) return dist[t];
for (int x=h[temp.num];x!=0;x=edge[x].next)
{
if (dist[temp.num]+edge[x].val
{
dist[edge[x].v]=dist[temp.num]+edge[x].val;
q.push(state(edge[x].v,dist[edge[x].v]));
}
}
}
return -1;
}
int main()
{
init();
printf("%d",Dijkstra());
return 0;
}
-------------------------------------------------------------------------------------------------------------------
UPDATE:感谢王队(@wyh2000)倾情付出调试1个多小时找到了错误。。。
[所以那个ggd的变量就是他乱搞的大家请无视]