总目录 > 6 数学 > 6.3 高精度计算
前言
同样也是接触甚早同时也使用很多的一个内容,但许多时候手头没有模板又不想打。。所以是时候来个正儿八经的模板了!
子目录列表
1、概念
2、数位存储
3、四则运算
6.3 高精度计算
1、概念
众所周知,int 类型变量是 2 ^ 31(10 ^ 9) 数量级的,long long 类型变量是 2 ^ 63(10 ^ 18) 数量级的,而如果我们需要更高位数的计算呢?这时候就需要用到高精度计算。
高精度计算(Arbitrary-Precision Arithmetic),是指运用一些算法结构来支持位数更高的数之间的运算。其本身难度不高,但代码细节多,实现方式也有诸多不同,但万变不离其宗的是,其本质均是通过按照数位对数进行拆分计算。下面进行介绍。
2、数位存储
① 顺序存储
一般情况下,我们对数的存储便是简单的一个萝卜一个坑 —— 一个 int 类型的 a 表示一个数;一个 int 类型的数组 b[100] 表示 100 个数。因为数据类型本身存在范围,在需要高位数运算时,我们大可不必将整个数全部塞入一个变量中。
我们声明两个 int 类型的数组 a, b,a[i], b[i] 分别表示第一、二个数的从低到高的第 i 位(不使用 a[0], b[0])。再声明一个 int 类型的数组 c,用来存储结果。以相加为例,如图所示:

只要学过竖式计算,这个计算过程应该不需多言。从最低位,即第 6 位开始按位相加,如果两个数相加大于 10,则向前进一位。具体到实现的话,即如果 a[i] + b[i] >= 10,则 c[i] = a[i] + b[i] - 10, c[i - 1]++;以此类推,直到计算完最高位,计算结束,如图所示,c 存储结果。
② 逆序存储
上述顺序存储很方便,却并非最为符合逻辑的存储方法。原因有三:
> 首先我们的所有计算都是从个位开始,而使用顺序存储,相当于从最大的下标开始计算,从逻辑上看是相反的,不过这还无伤大雅;
> 上述例子是两个数位数相等,而如果不等,假设 b 的位数为 4 位,直接从第 1 位存储显然是没有对齐各个位置的,则还需要加上移位的操作,使第二个数从第 3 位(即两者位数差 + 1)存储,不过这依旧是可以解决的;
> 最重要的一点是,如果我们的计算结果的位数高于这两个数,更高位的数何去何从?这一点在加减法上问题不大,因为数组还有一个下标 0,可以用来保存进借位结果,但是乘法就不是一个位置能解决的了。
避免上述大大小小的麻烦,逆序存储才是正解。以 762 * 2351 为例,如图所示:
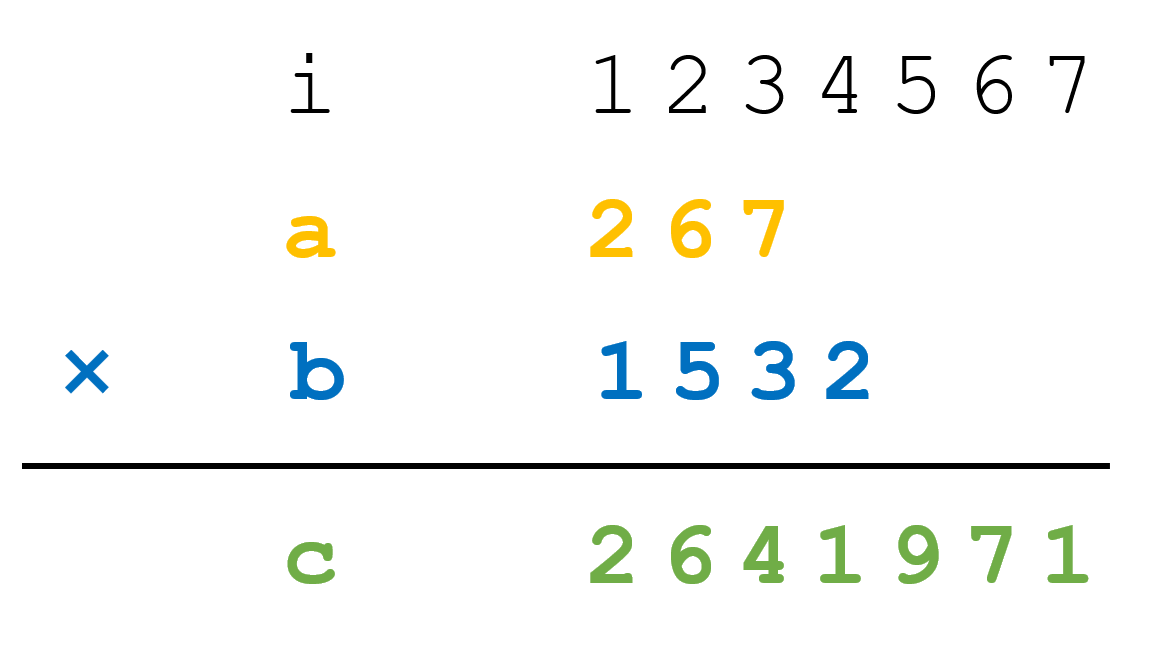
a[i], b[i], c[i] 分别表示第一、二个数和结果数的从高到低的第 i 位。可以看到,在乘法运算中结果位数可以超出很多,使用逆序存储,可以肆无忌惮地向后进位。同时,完全无需考虑两个数位数不同的情况。最后,将 c 所存储的内容逆序输出,即 1791462,为最终结果。
③ 压位存储
一个 int 类型的变量数据范围高达 2 ^ 31 数量级,我们却只拿它存储一个数字,是不是太浪费了?确实。但在空间、时间允许的情况下,这种一个变量存储一个数字的方法在操作起来是最为方便的。那如果不允许呢?后面我们有提到,在不压位的情况下,高精度加法、减法尚可接受,而高精度乘法时间复杂度高达 O(n ^ 2)。
压位存储,是一种以增加操作难度来换取运算效率提升的存储方法,即一个 int 变量存储若干位数字,至于到底多少位,因题而定,压得越多,复杂度越低,一般选择压 2 位或 4 位。比如对于 762 * 2351,如果使用压位存储(压 2 位),则 a = {0, 62, 7}, b = {0, 51, 23},再进行逐 2 位相乘以及进位。
3、四则运算
(下述代码都是从高精度计算封装类中节选出来,最终代码写在最后)
① 高精度加法
在上述介绍顺序存储时,已经有所提及了,加上本身也没太多难度,也就不再介绍了。
代码:
1 void add() { 2 for (int i = 1; i <= max(la, lb); i++) { 3 c[i] += (a[i] + b[i]) % 10; 4 c[i + 1] = (a[i] + b[i]) / 10; 5 } 6 outp(max(la, lb) + 1); 7 }
备注:
不支持负数运算。
② 高精度减法
在高精度加法的基础上,需要考虑结果为负数的情况。在计算之前就要判断这个情况,如果减数更大,我们可以将减数与被减数对调相减,最后在结果之前加上负号即可,因为 a - b = -(b - a)。先判断减数是否大于被减数,如果减数位数更高,则显然大于;如果位数更低,则小于;如果位数相等,则需从最高位逐位判断,任意一位减数大于被减数对应位时,说明减数更大。
代码:
1 bool minus() { 2 if (la < lb) return 1; 3 else if (la > lb) return 0; 4 else for (int i = 1; i <= la; i++) 5 if (a[i] < b[i]) return 1; 6 return 0; 7 } 8 void swap() { 9 int t = la; 10 for (int i = 1; i <= la; i++) 11 c[i] = a[i]; 12 memset(a, 0, sizeof(a)); 13 for (int i = 1; i <= lb; i++) 14 a[i] = b[i]; 15 memset(b, 0, sizeof(b)); 16 for (int i = 1; i <= la; i++) 17 b[i] = c[i]; 18 memset(c, 0, sizeof(c)); 19 la = lb, lb = t; 20 } 21 void dec() { 22 if (minus()) cout << '-', swap(); 23 for (int i = 1; i <= max(la, lb); i++) { 24 c[i] += a[i] - b[i]; 25 if (c[i] < 0) c[i] += 10, c[i + 1]--; 26 } 27 outp(max(la, lb) + 1); 28 }
备注:
不支持负数运算。
③ 高精度乘法
高精度乘法可以分为高精度 * 单精度和高精度 * 高精度两类。
高精度 * 单精度,即第二个数是个普通的 int 类型,那么问题很好想,我们对于第一个数每一位数字乘上这个数即可,然后和加法类似,进行进位。逐位相加最高不会超过 18,所以加法的进位只可能对更高一位产生 +1 的效果;而对于此处的乘法,其相乘结果可能远大于一个十位数,所以要进的位数可能不止一位。以 1337 * 42 为例,如图所示(原网站提供了一个画风很 jk 的图,这里就直接蒯辣):

对于个位,7 * 42 = 294,该位保留 294 % 10 = 4,下位进位 290 / 10 = 29(这里 / 表示整除);
对于十位,3 * 42 + 29 = 155,该位保留 155 % 10 = 5,下位进位 155 / 10 = 15;
以此类推,最终结果为 56154。
高精度 * 高精度,本质是相通的,只不过从单精度情况下的一个数的每一位对另一个数相乘变成了两个数的每一位均需要相乘,即 ai * bj * 10 ^ (i + j - 1),也就是说,对于 a[i] * b[j],其结果应该加到 c[i + j - 1] 。时间复杂度从 O(n) 暴增至 O(n ^ 2)。还是上述的 1337 * 42,还是原网站的图:

代码(高精度 * 高精度):
1 void mul() { 2 for (int i = 1; i <= la; i++) 3 for (int j = 1; j <= lb; j++) { 4 c[i + j - 1] += a[i] * b[j]; 5 if (c[i + j - 1] >= 10) 6 c[i + j] += c[i + j - 1] / 10, c[i + j - 1] %= 10; 7 } 8 outp(la + lb); 9 }
备注:
不支持负数运算。
④ 高精度除法
就像加法与乘法相通,减法与除法也是相通的。除法的计算过程可以理解为若干次减法,只不过相比前面,除法应该是四则运算中最麻烦的,不过只要你理解竖式长除法,其实也没什么难度。除法本身是从最高位计算的,而拆分出的若干次减法是从最低位开始计算。以 456 / 12 为例,如图所示:
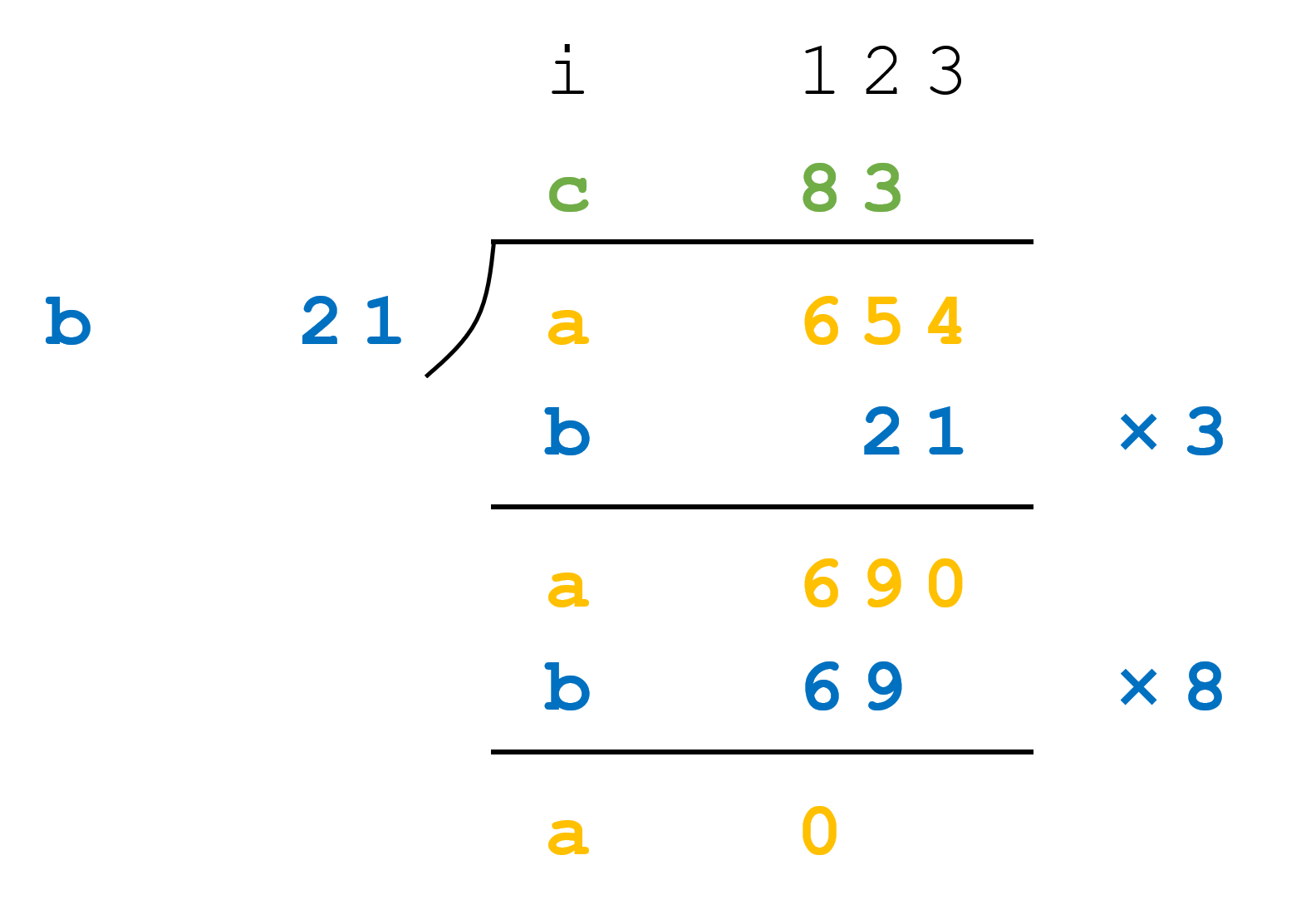
(因为为了对应所采用的逆序存储,此图并非传统意义上的竖式长除,只供分析具体过程)
从 a 的最高下标,即最高位开始,向前寻找共计 2 个位数(即 b 的位数)的位置,即 45。每次对 45 减去 12,直至再减就变成负数,则 45 总共减 3 次至 9,456 变成 96;
移至下一位,即 96。每次对 96 减去 12,总共减 8 次,96 变成 0。
综上,答案为 38。
判断是否还能再减时同减法时判断减数是否大于被减数一样逐位判断直到最后一位。注意,不仅需要判断当前的若干位数,还需要向前判断一位,因为可能存在上一次减法并没有完全减完。比如 36 / 2,首先对 3 减去 2,变成 1,移至下一位 6,减去 3 次 2 后变成 0,此时十位仍有 1,故还可以继续减,直至减满 8 次,最终答案为 18。
代码:
1 bool chk(int o) { 2 if (a[o + 1]) return 1; 3 for (int i = lb; i >= 1; i--) { 4 if (a[o - lb + i] < b[i]) return 0; 5 else if (a[o - lb + i] > b[i]) return 1; 6 } 7 return 1; 8 } 9 void div() { 10 for (int i = la; i >= lb; i--) { 11 int res = 0; 12 while (chk(i)) { 13 res++; 14 for (int j = 1; j <= lb; j++) { 15 a[i - lb + j] -= b[j]; 16 if (a[i - lb + j] < 0) 17 a[i - lb + j] += 10, a[i - lb + j + 1]--; 18 } 19 } 20 c[i - lb + 1] = res; 21 } 22 outp(la); 23 }
备注:
不支持负数运算。不返回余数。不支持非法运算提示。
4、封装类代码
1 #define MAXN 10005 2 3 class bigNum { 4 private: 5 int la, lb, lc; 6 public: 7 int a[MAXN], b[MAXN], c[MAXN]; 8 bigNum(char *ca, char *cb) { 9 la = strlen(ca); 10 for (int i = 1; i <= la; i++) 11 a[la - i + 1] = ca[i - 1] - '0'; 12 lb = strlen(cb); 13 for (int i = 1; i <= lb; i++) 14 b[lb - i + 1] = cb[i - 1] - '0'; 15 memset(c, 0, sizeof(c)); 16 } 17 int outp(int l) { 18 lc = l; 19 int lzero = 1; 20 for (int i = lc; i > 1; i--) { 21 if (lzero && !c[i]) continue; 22 else lzero = 0; 23 cout << c[i]; 24 } 25 cout << c[1]; 26 } 27 void add() { 28 for (int i = 1; i <= max(la, lb); i++) { 29 c[i] += (a[i] + b[i]) % 10; 30 c[i + 1] = (a[i] + b[i]) / 10; 31 } 32 outp(max(la, lb) + 1); 33 } 34 bool minus() { 35 if (la < lb) return 1; 36 else if (la > lb) return 0; 37 else for (int i = 1; i <= la; i++) 38 if (a[i] < b[i]) return 1; 39 return 0; 40 } 41 void swap() { 42 int t = la; 43 for (int i = 1; i <= la; i++) 44 c[i] = a[i]; 45 memset(a, 0, sizeof(a)); 46 for (int i = 1; i <= lb; i++) 47 a[i] = b[i]; 48 memset(b, 0, sizeof(b)); 49 for (int i = 1; i <= la; i++) 50 b[i] = c[i]; 51 memset(c, 0, sizeof(c)); 52 la = lb, lb = t; 53 } 54 void dec() { 55 if (minus()) cout << '-', swap(); 56 for (int i = 1; i <= max(la, lb); i++) { 57 c[i] += a[i] - b[i]; 58 if (c[i] < 0) c[i] += 10, c[i + 1]--; 59 } 60 outp(max(la, lb) + 1); 61 } 62 void mul() { 63 for (int i = 1; i <= la; i++) 64 for (int j = 1; j <= lb; j++) { 65 c[i + j - 1] += a[i] * b[j]; 66 if (c[i + j - 1] >= 10) 67 c[i + j] += c[i + j - 1] / 10, c[i + j - 1] %= 10; 68 } 69 outp(la + lb); 70 } 71 bool chk(int o) { 72 if (a[o + 1]) return 1; 73 for (int i = lb; i >= 1; i--) { 74 if (a[o - lb + i] < b[i]) return 0; 75 else if (a[o - lb + i] > b[i]) return 1; 76 } 77 return 1; 78 } 79 void div() { 80 for (int i = la; i >= lb; i--) { // 654 81 int res = 0; 82 while (chk(i)) { 83 res++; 84 for (int j = 1; j <= lb; j++) {// 21 85 a[i - lb + j] -= b[j]; 86 if (a[i - lb + j] < 0) 87 a[i - lb + j] += 10, a[i - lb + j + 1]--; 88 } 89 } 90 c[i - lb + 1] = res; 91 } 92 outp(la); 93 } 94 };
注意:
① 采用逆序存储,没有压位存储;
② 读入数据时通常采用字符数组,而计算时采用 int 类型数组更方便,所以构造函数内包含字符数组转化为 int 类型数组的代码(1.2 C++ 基础知识 提到的数据类型之间的互通性在这里就体现了出来);
③ 输出数据时结果位数是默认取最高情况,即加减法取原两个数中的较高位数加上一位;乘法取原两个数位数之和;除法取被除数位数。但显然可能位数会更低,这时候一定处理好前导 0(即出现在数之前多余无用的 0)不要输出。特别地,将最后一位单独输出而不进行前导 0 处理,因为可能存在结果为 0 的情况。