总目录 > 7 数据结构 > 7.4 堆与优先队列
前言
小时候,学长对我讲,堆和优先队列,是一个意思。一开始学了堆,然后一直手写堆;自从有一天被告知 STL 中的 priority_queue 就是堆之后,也就再也没写过堆了。
这里好好理清楚两者的概念,并回顾一下堆,再拓展一下更多的内容。
子目录列表
1、堆与二叉堆
2、二叉堆的存储与操作
3、堆排序
4、特殊的堆
5、优先队列
7.4 堆与优先队列
1、堆与二叉堆
堆是一种特殊的树,其每个结点的权值必须大于等于或小于等于其父亲结点的权值。也就是说,堆本身并不是一种数据结构,而是对树上结点权值有特定要求的一种树。
堆的种类很多,以二叉堆最为常见。通常我们提及的堆是狭义的二叉堆,所以不少地方会直截了当地定义为 “堆是一棵二叉树”,其实不够严谨。除了二叉堆,广义的堆还包括配对堆,左偏树,二项堆,斐波那契堆等,它们并不全是二叉堆。
堆与二叉堆的关系同树与二叉树一样 —— 二叉堆是所有结点至多只有 2 个儿子结点的堆,是一棵具有堆性质的二叉树。同时,它还有一个性质 —— 所有叶子结点都处于深度最大或次大的层次,即完全二叉树。
根据父子结点大小关系,二叉堆可以分成两类:
> 大根堆:结点权值小于等于父亲结点权值
> 小根堆:结点权值大于等于父亲结点权值
比如下面两棵树,分别为大根堆和小根堆。

2、二叉堆的存储与操作
下面的内容均以大根堆为例。
① 存储
在二叉树部分(7.3 树与二叉树)已经介绍了二叉树的顺序与链式存储结构,堆属于完全二叉树,所以使用顺序存储更方便。下面的二叉堆操作代码均为顺序存储。
② 插入
> 概念
向二叉堆插入一个元素,插入后依旧保持堆性质。
> 思路
在最下一层最右侧叶子结点后插入,如果已经是满二叉树,则新增一层。此时,树仅满足完全二叉树性质,而不满足堆性质,则需要向上调整。
从插入的结点开始,如果该结点权值大于父亲结点,则两个结点交换,重复该过程,直到满足堆性质。向上调整过程时间复杂度为 O(log n)。
> 代码
void insert(int x) { tot++; int o = x; while (a[o] > a[fa] && o != 1) swap(a[o], a[fa]), o = fa; }
③ 删除
> 概念
删除堆中最大的元素,即根结点,删除后依旧保持堆性质。
> 思路
如果直接删除,则变成了两个堆,不满足堆性质,则需要向下调整。
我们将当前根结点与最后一个结点交换,并删除最后结点(即原根结点),当前该根结点不一定满足堆性质,则从该结点开始,找到其子结点中最大的,两个结点交换,重复该过程,直到子结点均小于该结点,或到达最下一层。向下调整过程时间复杂度为 O(log n)。
> 代码
void del() { int o = 1; a[1] = a[tot], a[tot] = 0, tot--; while (ls <= tot) { if (a[o] > max(a[ls], a[rs])) break; if (a[ls] > a[rs]) swap(a[o], a[ls]), o = ls; else swap(a[o], a[rs]), o = rs; } }
④ 构造
> 概念
给出一个数列,将数列各个数放入堆中。
> 思路
将数列的数逐一插入即完成构造,即向上调整法;同样也可以选择向下调整法。
> 代码
略。
3、堆排序
以大根堆为例,将有 n 个元素的数列构造为堆,每次取出的根结点为当前最大值,取出 n 次,即完成从大到小的排序。时间复杂度为 O(n log n)。
代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 100005 5 #define ls o << 1 6 #define rs o << 1 | 1 7 #define fa o >> 1 8 9 int n; 10 11 class Heap { 12 public: 13 void insert(int x) { 14 tot++; 15 int o = x; 16 while (a[o] > a[fa] && o != 1) 17 swap(a[o], a[fa]), o = fa; 18 } 19 int top() { 20 return a[1]; 21 } 22 void del() { 23 int o = 1; 24 a[1] = a[tot], a[tot] = 0, tot--; 25 while (ls <= tot) { 26 if (a[o] > max(a[ls], a[rs])) break; 27 if (a[ls] > a[rs]) 28 swap(a[o], a[ls]), o = ls; 29 else 30 swap(a[o], a[rs]), o = rs; 31 } 32 } 33 void outp() { 34 for (int i = 1; i <= tot; i++) 35 cout << a[i] << ' '; 36 cout << endl; 37 } 38 int a[MAXN]; 39 static int tot; 40 } h; 41 42 int Heap :: tot; 43 44 int main() { 45 cin >> n; 46 for (int i = 1; i <= n; i++) 47 cin >> h.a[i], h.insert(i); 48 while (h.tot) 49 cout << h.top() << ' ', h.del(); 50 return 0; 51 }
4、特殊的堆
除了二叉堆,堆家族里还有配对堆,左偏树,二项堆,斐波那契堆等等。
暂时放个原网站的图。
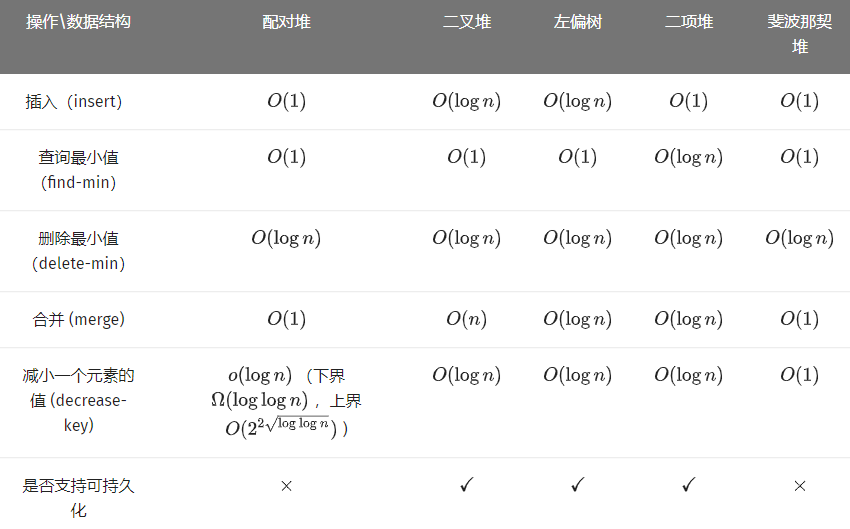
5、优先队列
小明楼下有两家包子店,一家平价包子店,大家先排队的先买到包子,这样的队即普通的队列;一家贵族包子店,对于一列排队的人,店小二每次从中选出位置最高的辣个人让他先买包子,正所谓贵族优先,这样的队列我们称之为优先队列。
优先队列是一种特殊的队列,但并不满足普通队列的 FIFO 原则,而是根据设定的优先级来出队。最简单的,如果队列中存储的是 int 类型变量,优先级可以为较小值,即每次出队值最小的元素,反之同理,也可以为较大值。
我们发现,队列用数组实现是很轻松的,只需要两个 head, tail 两个指针就能表示入队出队操作;而对于优先队列,我们需要动态维护当前队列内优先级最高的元素,使用简单的数组显然是复杂度爆炸的,这时候,我们抬头看看上面介绍的堆,一切都变得明朗起来。
堆的特性注定了它的不凡 —— 对于大根堆,其根结点必然是整棵树的最大权值,正好满足我们优先队列在优先级设定为最大值时的需求,且动态维护这个最大值效率很高。小根堆同理。所以,优先队列的出队操作,和堆的取出根结点元素操作是等价的,这就是为什么之前会认为堆和优先队列是一个东西,因为相关性实在太强,但是,它们的正确关系应该为:
优先队列这个数据结构是通过堆来实现的。
C++ 的 STL 中有对优先队列的直接实现,即 priority_queue,它的构造方式为:
priority_queue <Typename T, Container, Functional> q;
STL 优先队列是使用二叉堆的最大堆实现的。当然,可以通过重载运算符将其更改为最小堆,以及支持对非常规变量的比较。无独有偶,Java 中也内置了 java.util.PriorityQueue,不同的是它内置的是最小堆,同样可以通过比较器来更改为最大堆。