总目录 > 7 数据结构 > 7.5 Huffman 哈夫曼树
前言
这是一篇原网站没有涉及到的知识点,很久之前也学过了,趁着数据结构课要做实验就再复习下好啦。
子目录列表
1、最优二叉树
2、构造方法
3、哈夫曼编码
4、译码
5、代码
7.5 Huffman 哈夫曼树
1、最优二叉树
哈夫曼树(Huffman Tree),又名最优树,是一类带权路径长度最短的树,应用比较广泛。这里我们暂时只讨论最优二叉树。
先给出几个概念:
路径:从树中一个结点到另一个结点之间的分支构成两个结点之间的路径;
路径长度:路径上的分支数目;
树的路径长度:从根结点到每一个结点的路径长度之和。
哈夫曼树的特点在于,有且仅有叶子结点带权,比如:
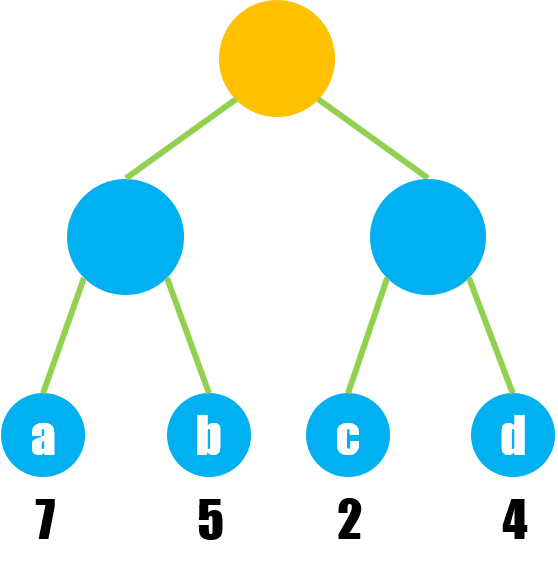
带权路径长度:根结点到该结点的路径长度与结点权值的乘积;
树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记作:
WPL = ∑ w[k] * l[k]
其中,k ∈ [1, n],n 表示结点个数,w[k] 表示结点 k 的权值,l[k] 表示结点 k 到根结点的路径长度。
扯了这么多,回到最开始的定义:哈夫曼树是带权路径长度最短的树,即给出若干个结点构造一棵树,当且仅当其 WPL 是所有构造方式中最小的,就是哈夫曼树,例如上图的 4 个字符 {a, b, c, d},其三种构造方式:
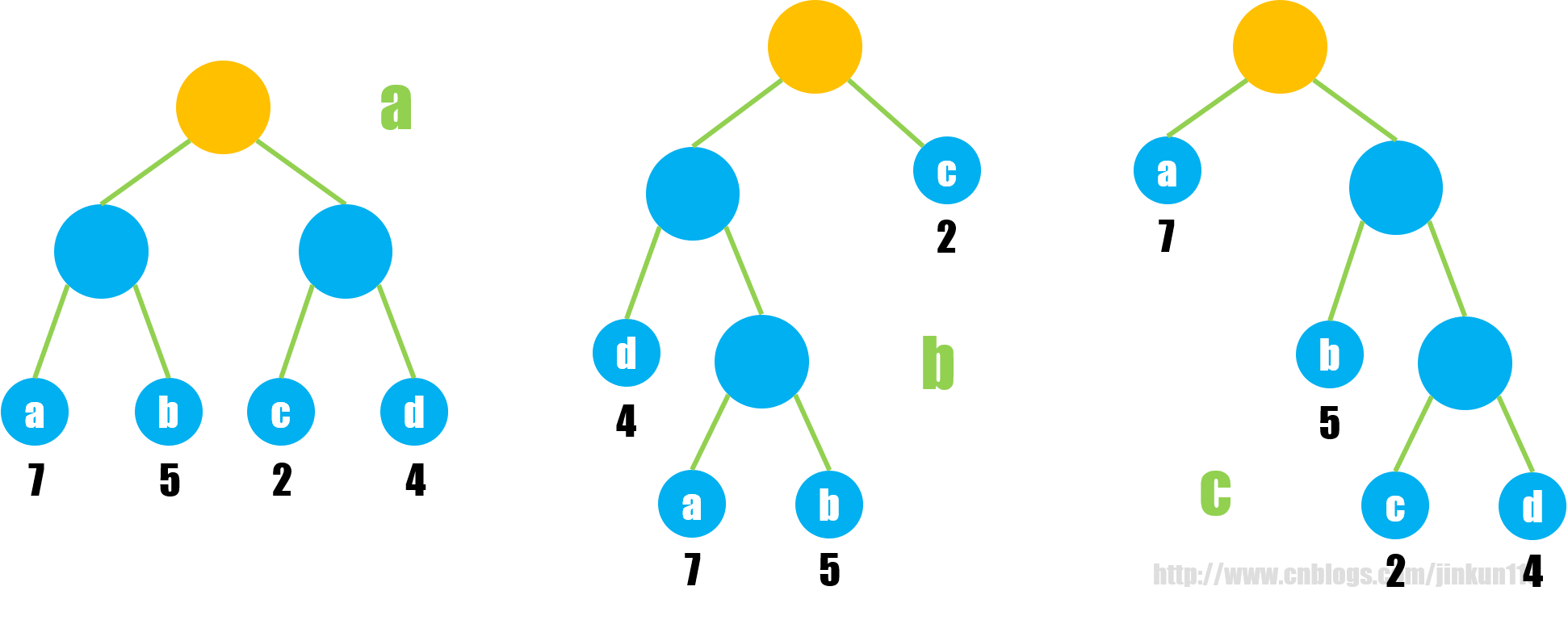
图 a 对应:WPL = 7 * 2 + 5 * 2 + 2 * 2 + 4 * 2 = 36
图 b 对应:WPL = 7 * 3 + 5 * 3 + 2 * 1 + 4 * 2 = 46
图 c 对应:WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3 = 35
我们发现,图 c 所表示的树正是哈夫曼树。
2、构造方法
给出 n 个带权结点,第 i 个结点权值为 w[i]。
① 将 n 个结点视作 n 棵二叉树,有且仅有一个根结点,根结点权值为 w[i],全部放入二叉树集合 T;
② 构造一棵新二叉树。从 T 中选择两棵根结点最小的树,分别作为这棵新二叉树的左右子树;
③ 将新二叉树加入集合 T,将被选择的两棵原二叉树移除;
④ 反复执行 ② 和 ③,直到 T 中只有一棵树。此时,这棵树即为哈夫曼树。
3、哈夫曼编码
说了这么多,还没有看出哈夫曼树的意义在哪?
数字国和字母国因为争论谁是世界霸主而掀起一场旷世大战。数字国在字母国安插了许多间谍,有一天一个间谍截获了一份字母国写满了字母的机密文件,想要通过用电文传回给数字国,但担心被字母国发现,于是决定将字母全部转化为 0 和 1 两个数字,现在他需要考虑一个最合适的转换方案,使其发送的电文尽可能短。
我们假设这份机密文件只有 "abaccda" 这 4 种字符,7 个字母。最朴素的编码方案为:
a - 00, b - 01, c - 10, d - 11,则电文为:00010010101100,共 14 位,对方接收后,直接将其两位两位断开,即可获得原文。
但是否存在更优解?我们这样编码:
a - 0, b - 1, c - 10, d - 11,则电文为:0101010110,共 10 位,确实短了,却出现了一个致命的问题:由于编码方案不等长,对方并不能直接等长隔断;同时,a 的编码是 c, d 的前缀,字母之间存在歧义,比如如何告知对方,10 到底表示的是 c 还是 ba?所以,我们需要保证任何一个字符的编码都不是另一个编码的前缀,这种编码称作前缀编码。再来一次:
a - 0, b - 10, c - 110, d - 111,则电文为:0100110110111,共 13 位,没有任何理解问题,但是,这仍然并非最优解。
我们发现,在短短 7 个字母中,a 出现了 3 次,c 出现了 2 次,而 b, d 只有 1 次;我们如果希望总长度尽可能短,那么就应该使出现频率较高的采用较短的编码,频率较低的采用较长的编码,比如:
a - 0, b - 110, c - 10, d - 111,则电文为:011001010111,共 12 位,为最优解,即哈夫曼编码。
那么如何得到这样的哈夫曼编码?
假设现在有 n 个字符,第 i 个字符出现的频数为 w[i],将其作为字符的权值,再直接套用上面的哈夫曼树构建方式就行,因为哈夫曼树的构建过程,本质就是使权值较大的结点极可能离根结点近,构建完后只需要对每一个结点连接左右子树的两条边分别标上 0, 1,就能很轻松地得到每一个字符的哈夫曼编码了,比如:
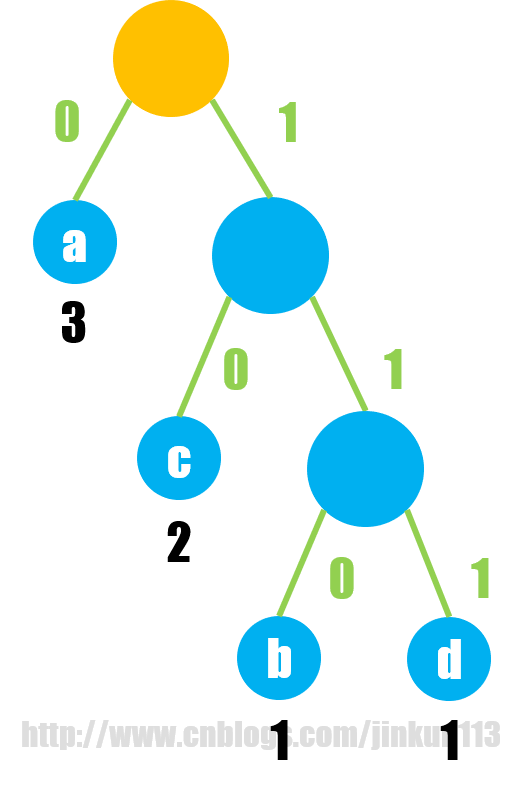
和上述推断出的哈夫曼编码一致。
因为所有字符之间不存在直接的祖先关系,所以不存在一个字符的编码是另一个字符编码的前缀的情况。
4、译码
数字国高层收到了间谍发来的情报,是一串数字加一棵树。可惜数字国高层都是丈育,他们不知道该怎么处理这个数字电文。
还是上面的例子,电文为:011001010111。从第1位开始,根据编码是0还是1在树上进行搜索,如果是0则向左子树搜索,反之向右子树搜索,直到找到了叶子结点,即译得了一个字符,并退出本次查找;以此反复,直到遍历完成,即完成对该哈夫曼编码的译码过程。
5、代码
直接把实验报告里这个带注释的复制过来辣。
注意,这个代码仅适用于小写字母的编码,要更广的适用性还需进行修改。
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 55 5 6 class Tree { 7 public: 8 int root, ls, rs, w; // 分别表示子树根结点序号,左儿子结点,右儿子结点,根结点权值 9 Tree(int _root, int _ls, int _rs, int _w): 10 root(_root), ls(_ls), rs(_rs), w(_w) {} 11 Tree(): root(0), ls(0), rs(0), w(0) {} 12 void init(int); 13 friend bool operator < (Tree a, Tree b) { 14 return a.w > b.w; 15 } 16 } t[MAXN]; 17 18 int n, tmp[MAXN]; 19 int* code[MAXN]; 20 char ch[10005]; 21 priority_queue <Tree> Q; // 优先队列,用于每次找出根结点权值最小的两棵子树 22 23 void Tree :: init(int o) { // 初始化结点,将结点放入优先队列 24 cin >> w, root = o; 25 Q.push(t[o]); 26 } 27 28 void coding() { // 哈夫曼编码函数 29 for (int i = 1; i < n; i++) { 30 Tree t1 = Q.top(); Q.pop(); 31 Tree t2 = Q.top(); Q.pop(); // t1, t2分别是根结点权值最小的两棵子树,从优先队列中弹出 32 t[i + n] = (Tree) {n + i, t1.root, t2.root, t1.w + t2.w}; 33 Q.push(t[i + n]); // 将合并的新二叉树加入优先队列 34 } 35 } 36 37 void dfs(int o, int d) { // 树的遍历函数 38 if (o <= n) { // 如果是叶子结点 39 code[o] = (int*) malloc((d + 1) * sizeof(int)); // 动态分配数组内存 40 for (int i = 1; i < d; i++) 41 code[o][i] = tmp[i]; // 将存储在tmp中的01序列复制到字符o的哈夫曼编码数组 42 code[o][d] = 2; // 结束标志,用于输出编码 43 return; 44 } 45 tmp[d] = 0, dfs(t[o].ls, d + 1); 46 tmp[d] = 1, dfs(t[o].rs, d + 1); 47 } 48 49 void getCode() { // 输出编码函数 50 dfs(2 * n - 1, 1); // 从根结点开始遍历 51 for (int i = 1; i <= n; i++) { 52 int o = 1; 53 cout << (char)(i + 'a' - 1) << ' '; 54 while (code[i][o] != 2) cout << code[i][o], o++; // 输出编码,直到出现结束标志 55 cout << endl; 56 } 57 } 58 59 void translate() { // 译码函数 60 while (1) { 61 cin >> ch; 62 int l = strlen(ch), o = 2 * n - 1; 63 for (int i = 0; i < l; i++) { 64 if (ch[i] == '0') o = t[o].ls; // 如果是0,向左儿子搜索 65 else o = t[o].rs; // 反之向右儿子搜索 66 if (o <= n) { // 如果是叶子结点 67 cout << (char)(o + 'a' - 1); 68 o = 2 * n - 1; // 重新从根结点开始搜索 69 } 70 } 71 } 72 } 73 74 int main() { 75 cin >> n; 76 for (int i = 1; i <= n; i++) t[i].init(i); 77 coding(); 78 getCode(); 79 translate(); 80 return 0; 81 }