【算法】冒泡排序

#第一次，找到最大值

n=[3,5,1,6,2]

for i in range(len(n)-1):

    if n[i]>n[i+1]:

        n[i],n[i+1]=n[i+1],n[i]

print (n[-1])

#第二次，找到次大值，放在倒数第二的位置

n=[3,1,5,2,6]

for i in range(len(n)-1-1):

    if n[i]>n[i+1]:

        n[i],n[i+1]=n[i+1],n[i]

print (n[-2])

#第三次，找第三个最大数

n=[1,3,2,5,6]

for i in range(len(n)-1-1-1):

    if n[i]>n[i+1]:

        n[i],n[i+1]=n[i+1],n[i]

print (n[-3])

#第四次，找第四个最大数

n=[1,2,3,5,6]

for i in range(len(n)-1-1-1-1):

    if n[i]>n[i+1]:

        n[i],n[i+1]=n[i+1],n[i]

print (n[-4])

#冒泡排序最终

a= [3,5,1,6,2]

for i in range(len(a)-1):           #0,1,2,3

    for j in range(len(a)-1-i):      #4-0；4-1；4-2；4-3

        if a[j]>a[j+1]:

            a[j],a[j+1] = a[j+1],a[j]

print(a)

第一次内层循环的结果就是找到最大的值

第二次内层循环的结果就是找到次大的值,本次将忽略最后一个元素的比较

第二次内层循环的结果就是找到第三大的值，本次讲忽略倒数第二个元素和最后一个元素的比较

.......

1、冒泡排序图示

 

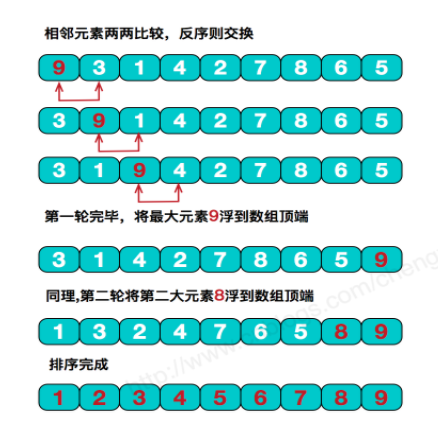
#练习：在上面排序的基础上，将最小的放在后面，最大的放在前面

a= [3,2,1,9,56,48,20,4,9,6,0]

for i in range(len(a)-1):      

    for j in range(len(a)-1-i):    

        if a[j]<a[j+1]:

            a[j],a[j+1] = a[j+1],a[j]

print(a)

或者直接

a= [3,2,1,9,56,48,20,4,9,6,0]

for i in range(len(a)-1):         

    for j in range(len(a)-1-i):   

        if a[j]>a[j+1]:

            a[j],a[j+1] = a[j+1],a[j]

print(a[::-1])

2、冒牌排序原理

冒泡排序的基本思想是，对相邻的元素进行两两比较，顺序相反则进行交换，这样，每一趟会将最小或最大的元素“浮”到顶端，最终达到完全有序

3、冒泡算法的时间复杂度

时间复杂度从小到大的排序顺序为：

常数阶O(1),对数阶O( log n ),线性阶O(n),平方阶O(n^2)，立方阶O(n^3),...，k次方阶O(n^k),指数阶O(2^n)。随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。也就是：
O(1) < O(logn) < O(n) < O(nlogn)<O(n^2) < O(n^3) <…< O(n^k)<O(2^n) <O(n!)

对于算法来讲，只看影响最大的那个因子是什么（怎么判断哪个因子是影响最大的？），一般忽略分母，不看分母

#练习：计算冒泡排序的时间复杂度

遍历第1遍时，比较了n-1次；

遍历第2遍时，比较了n-2次；

遍历第3遍时，比较了n-3次；

遍历第4遍时，比较了n-4次；

……….

遍历第n-1遍时，比较了1次；

综上，总共比较的次数为1+2+3+4+….+(n-1)=n(n-1)/2次

因为，n(n-1)/2=n^2/2-n/2

所以，他的时间复杂度为O(n^2)