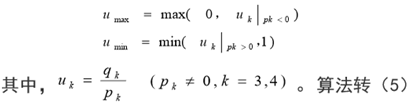裁剪算法

Cohen-Sutherland算法（编码裁剪算法）

一、基本思想

采用编码的方式对直线段分三种情况处理

(3)重点在于2种情况都不满足的时候，需要按交点来进行分段，然后再判定。

二、编码规则

(1)以上三种情况都采用编码的方式来快速解决。

每条线段的端点偶读赋以四位二进制码D₃D₂D₁D₀，编码规则如下：

左右下上，即边界之外为1，否则为0。

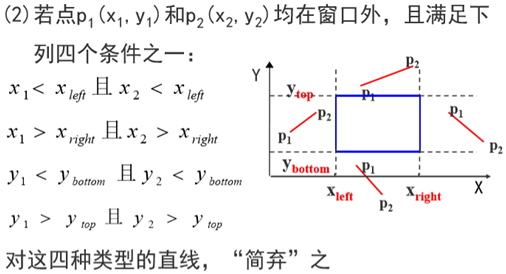
(2)

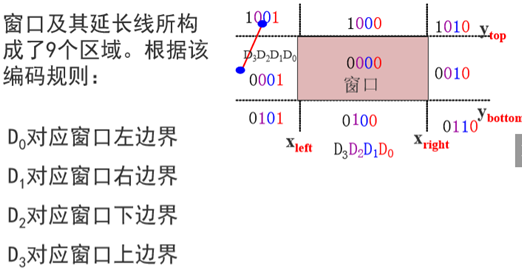
三、具体实现

裁剪出一条线段，先求出端点编码code1和code2，然后进行“或” 和“与” 运算。

或0取，与非弃。

(3)若以上2种情况都不满足，例如：

此时将p₁和p₂的编码进行与或操作发现，或不为0，与为0。则采用分段的方法。按左右下上的顺序求出交点P₃，P₁P₃在窗外则舍弃。

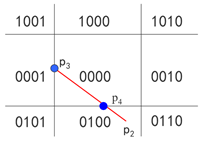
得到p₃p₂时，再对p₃p₂进行编码测试，发现也属于第三种情况。则再求出交点p₄。经测试，p₃p₄可取，p₄p₂舍弃。

四、额外说明

(1)虚交点：对于舍弃的情况还有一种特例，如下图中的蓝线。

此时AB点进行编码测试也属于第三种情况，但是却需要舍弃。这就需要计算出虚交点，然后分段舍弃了AC和CB。

(2)交点的计算方法

因为通常都是已经边界坐标，所以都是利用斜率来按照左下右上的顺序计算交点。

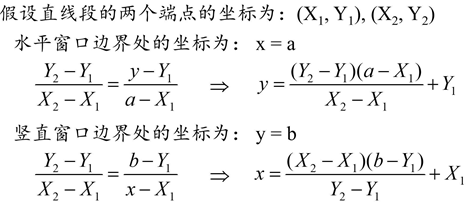
 中点分割算法

一、基本思想

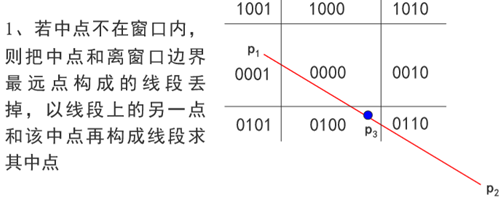
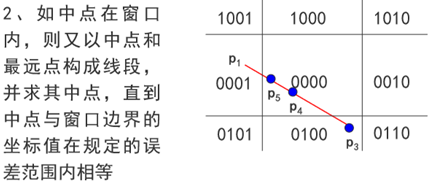
中点分割用到的测试方法仍然是编码测试，但是用二分逼近来确定直线段与窗口的交点。而具体的实现，也是根据中点的位置情况来讨论的。

二、具体实现

何为误差范围？

比如在1024的分辨率下，最多也就进行10次二分，不可能永远分下去。所以需要提前设定误差范围。

中点分割算法相比于Cohen-Sutherland算法，避免了求交，只需计算中点坐标即可完成，宜于硬件实现 。

Liang-Barsky算法

一、基本思想

 把被裁剪直线看成一条有向线段并用参数方程表示，进而确定出要获取的部分。

1.参数表示

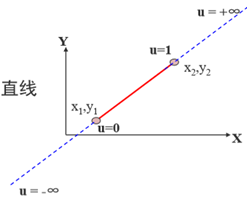
2.方向设定确认点

将四条边分为入边和出边

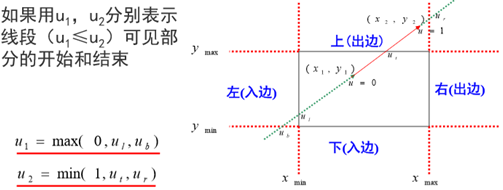
u₁u₂则为裁剪区域内的线段

3.不等式变换

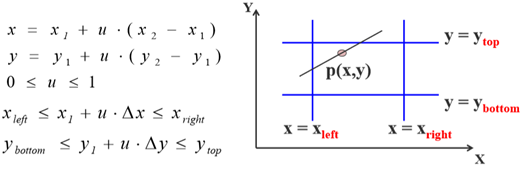
裁剪区域内的点可由以上不等式得到，移项变换得

我们可以

4.分类讨论

(1)p_k=0

a. p₁&p₂=0，此时直线垂直，若q₁<0或q₂<0则直线在裁剪区域外，直接舍弃。

                           

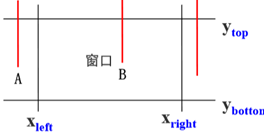
b.  p₃&p₄=0，此时直线平行，若q₃<0或q₄<0则直线在裁剪区域外，直接舍弃。

                         

c.  p₁&p₂=0且q₁≥0或q₂≥0，p₃&p₄=0且q₃≥0或q₄≥0（即上图B和F的情况）。则进一步根据交点判断。

(2)p_k≠0

此处根据具体的ΔxΔy数据来得到pk的正负

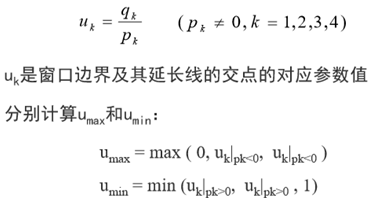
如图，此种情况为舍弃。u1>u2

二、具体实现