排序算法（七） —— 快速排序

快速排序（Quick Sort），有时又称划分-交换排序（Partition-Exchange Sort），与“归并排序”相同，是“分治法”的又一个实现案例。

快速排序的主要思想是，选取一个数字，通过一次遍历，将这个数字放到其最终的位置，并且保证其最终位置的左侧都小于等于这个数字，其右侧都大于等于这个数字。

一个优秀的快速排序实现，能比其竞争对手（归并排序，堆排序，都是时间复杂度为 O(nlog2n) 的排序算法），快2-3倍。

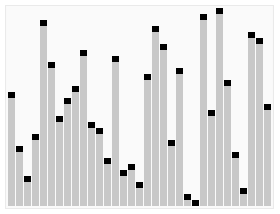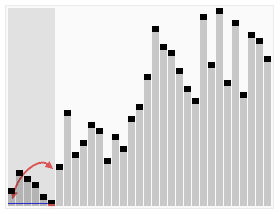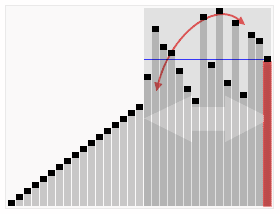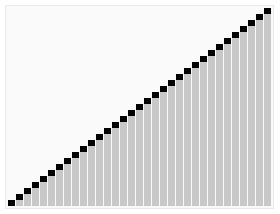
From Wikipedia： https://en.wikipedia.org/wiki/Quicksort

1. 快速排序的具体步骤

快速排序的过程可以拆分成以下三个步骤：

• 从数组中选择一个数字。
• 根据这个数字，对整个数组进行一次划分，即：通过一系列的交换，将这个数字放到其最终位置，并且保证其左侧的数字都小于等于它，右侧的数字都大于等于它。
• 对两侧的子数组进行递归。

2. 快速排序的基本代码

public abstract class BasicQuickSort implements Sort {

    @Override
    public void sort(int[] array) {
        sort(array, 0, array.length - 1);
    }

    private void sort(int[] array, int left, int right) {
        if (left < right) {
            int q = partition(array, left, right);
            sort(array, left, q - 1);
            sort(array, q + 1, right);
        }
    }

    protected abstract int partition(int[] array, int left, int right);
}

3. 划分 - 挖坑取数

从上述代码中不难发现，快速排序的核心内容是，如何对一个数组进行一次划分（partition）。

这里先介绍一种常见的划分算法，我称之为“挖坑取数”，具体过程如下：

• 将最左侧的数字作为待划分的数字，在快速排序中，称这个数字是划分的主元（pivot）。
• 从最右侧开始向前寻找，找到第一个比 pivot 小的数字（坑），交换 pivot。
• 此时，“坑”的位置被交换到了最左侧，从最左侧的下一个位置开始向后寻找，找到第一个比 pivot 大的数字，交换 pivot。
• 循环从两侧“夹逼”找“坑”的步骤，直至 pivot 到它的最终位置。

public class QuickSort2 extends BasicQuickSort {

    @Override
    protected int partition(int[] array, int left, int right) {
        int pivot = array[left];
        int i = left;
        int j = right + 1;
        boolean forward = false;
        while (i < j) {
            while (forward && array[++i] <= pivot && i < j) ;
            while (!forward && array[--j] >= pivot && i < j) ;
            ArrayHelper.swap(array, i, j);
            forward ^= true;
        }
        return j;
    }
}

　　

其中在“夹逼”过程中的最后一个判断 i < j，是为了防止在夹逼的过程中出现左侧小于右侧的情况。

退出循环后 i = j，所以最后一次交换也不会影响结果。

4. 划分 - 挖坑取数 - 演示步骤

如果上面的说明过于抽象，这里演示一遍“挖坑取数”在数组 {3, 5, 1, 9, 8, 6, 0, 2, 4, 7} 的执行步骤：

• 取 pivot=3。
• 从最右侧 7 开始，向前寻找，找到第一个小于等于 3 的数字：2，交换两者位置，得到数组： {2, 5, 1, 9, 8, 6, 0, 3, 4, 7} 。
• 从最左侧的下一个数字 5 开始，向后寻找，找到第一个大于等于 3 的数字：5，交换两者位置，得到数组： {2, 3, 1, 9, 8, 6, 0, 5, 4, 7} 。
• 从最右侧的上一个数字 0 开始，向前寻找，找到第一个小于等于 3 的数字：0，交换两者位置，得到数组： {2, 0, 1, 9, 8, 6, 3, 5, 4, 7} 。
• 从最左侧的下一个数字 1 开始，向后寻找，找到第一个大于等于 3 的数字：9，交换两者位置，得到数组： {2, 0, 1, 3, 8, 6, 9, 5, 4, 7} 。
• 从最右侧的上一个数字 6 开始，向前寻找，找到第一个小于等于 3 的数字，没有找到，得到最终数组：{2, 0, 1, 3, 8, 6, 9, 5, 4, 7}。
• 此时，pivot=3 的左侧数字全部小于等于3，右侧数字全部大于等于3，划分完成。

5. 划分 - 快慢指针

这里介绍另外一种划分算法，我称之为“快慢指针”，具体过程如下：

• 将最右侧的数字作为主元。
• 使用两个指针 faster 和 slower，faster 初始指向第一个数字，slower 初始时指向 faster 上一个数字。
• 从第一个数字开始遍历数组，快指针随着数组遍历的过程增大。
• 遍历数组时，每当数字小于等于 pivot 时，慢指针前进一位，然后交换快慢指针的位置，即慢指针指向的数字，永远小于等于 pivot。
• 当遍历结束时，0-慢指针的最终位置，都保证小于等于 pivot。快指针的最终位置，为 pivot 的前一位。
• 慢指针向前移动一位（指向的数字保证大于等于 pivot，只有指向 pivot 时，等号成立），交换 pivot 与此时慢指针的位置。

public class QuickSort1 extends BasicQuickSort {

    @Override
    protected int partition(int[] array, int left, int right) {
        int pivot = array[right];
        int slower = left - 1;
        for (int faster = left; faster < right; ++faster) {
            if (array[faster] <= pivot) {
                slower++;
                ArrayHelper.swap(array, slower, faster);
            }
        }
        ArrayHelper.swap(array, slower + 1, right);
        return slower + 1;
    }
}

6. 划分 - 快慢指针 - 演示步骤

同样地，演示一遍“快慢指针”在数组 A = {3, 5, 1, 9, 8, 6, 0, 2, 4, 7} 的执行步骤：

• 取 pivot=7，快指针初始位置指向 3，faster=0，慢指针初始位置在快指针的前一个位置，slower=-1。
• 第一个数，3 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 9, 8, 6, 0, 2, 4, 7}，slower=0，faster=1。
• 第二个数，5 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 9, 8, 6, 0, 2, 4, 7}，slower=1，faster=2。
• 第三个数，1 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 9, 8, 6, 0, 2, 4, 7}，slower=2，faster=3。
• 第四个数，9 > 7，慢指针位置不动 -> 保持原来的位置不变 -> 快指针前进一位，得到数组：{3, 5, 1, 9, 8, 6, 0, 2, 4, 7}，slower=2，faster=4。
• 第五个数，8 > 7，慢指针位置不动 -> 保持原来的位置不变 -> 快指针前进一位，得到数组：{3, 5, 1, 9, 8, 6, 0, 2, 4, 7}，slower=2，faster=5。
• 第六个数，6 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 6, 8, 9, 0, 2, 4, 7}，slower=3，faster=6。
• 第七个数，0 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 6, 0, 9, 8, 2, 4, 7}，slower=4，faster=7。
• 第八个数，2 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 6, 0, 2, 8, 9, 4, 7}，slower=5，faster=8。
• 第九个数，4 ≤ 7，慢指针前进一位 -> 交换快慢指针的位置 -> 快指针前进一位，得到数组：{3, 5, 1, 6, 0, 2, 4, 9, 8, 7}，slower=6，faster=9。
• 此时，快指针 faster=9，不满足小于 right=9 的条件，退出循环，将主元 pivot=7，与慢指针的先一个数字 A[7] = 9，做一次交换，得到最终数组：{3, 5, 1, 6, 0, 2, 4, 7, 8, 9}，划分完成。

7. 快速排序的时间复杂度和稳定性

• 最坏情况时间复杂度 T(n) = O(n^2)。
• 最好情况时间复杂度 T(n) = O(nlog2n)。
• 平均情况时间复杂度 T(n) = O(nlog2n)。
• 最坏情况空间复杂度 T(n) = O(n)。
• 最好情况空间复杂度 T(n) = O(log2n)。

• 快速排序，始终只使用原来的数组空间 O(1)，真正消耗的空间，是由递归的深度决定的。
• 无论哪一种快速排序排序的划分算法，都会打破快速排序的稳定性。

8. 快速排序的性能瓶颈与优化策略

详情见：排序算法杂谈（五） —— 关于快速排序的优化策略分析

Source Code: https://github.com/Gerrard-Feng/algorithm-learning.git