常见排序__总结

文章来自：http://www.iteye.com/topic/1129454

一、概括

1.冒泡排序

（1）基本思想：在一个序列元素中，比较相邻的两个数，如果相邻的数的顺序与想要输出的顺序相反就要进行交换，到序列末尾有序列中的最大值或者最小值在数组的一端。

（2）实例：

（3）优缺点：基本思想是元素之间两两进行比较，一趟排序之后，会有较小的数排在二者比较中前一个，最大的数排在后面，（会有最小的数排在前面，较大的数排在后面）。

缺点1是：每次一趟排序之后只有一个极值能达到真正的位置，比如最小的那个值或者最大的那个值。但是其余元素却不能保证，而且元素之间已经进行了两两交换。

缺点2是：另外一个是，当序列中大部分是有序的时候，剩下的一半还是需要进行迭代比较，虽然没有进行交换，但是却进行了相应的比较；

可以通过对外层循环进行优化，比如当剩余序列都是有序的，我们在内层循环外设置标志，当剩余序列存在逆序对时，标志位1，当剩余序列有序的时候，标志位为0；在内层循环结束，也是进行一趟完整的排序结束后；对标志位进行判断，如果为0，则标识剩下的序列已经是有序的，无需再继续外层循环，直接返回结果。这样做优化了缺点2.

（4）性质:时间复杂度为O（n*n），空间复杂度为O（1），稳定性为稳定。

（5）Java代码实现

 package sorts;

public class 冒泡排序 {
    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        changeSort(a);
    }

    private static void changeSort(int[] a) {
        int temp;
　　　　　int k = a.length-1;
　　　　　int flag = 0；
　　　　　int pos = 0;
        for(int i=0; i<a.length; i++){
　　　　　　　　// 是否发生交换标志
　　　　　　　　flag = 0；
            for(int j=0；j<k; j++){
                if(a[j]>a[j+1]){
                    temp = a[j];
                    a[j] = a[j+1];
                    a[j+1] = temp;
　　　　　　　　　　　　// *发生了交换 （优化点1）
　　　　　　　　　　　　flag = 1;
　　　　　　　　　　　　// *下次循环的最大坐标更新，这样做优化了比较次数（优化点2）
　　　　　　　　　　　　pos = j;

                }
            }
　　　　　　// 把更新后的最大的可比较坐标放到内层循环的判断条件中
　　　　　　k = pos;
　　　　　　// 如果这一轮的内层循环之后没有发生交换，说明序列已经有序无序继续进行外层循环，返回结果即可。
　　　　　　if(flag == 0){
　　　　　　return;
}

        }
　　　　// 打印数据排序后的结果
        for(int k=0; k<a.length; k++)
            System.out.println(a[k]);
    }
}

2.快速排序

http://blog.csdn.net/insistgogo/article/details/7785038

（1）基本思想：

1.选择一个哨兵（序列中的第一个元素），序列中有两个标识元素分别指向序列的头部和尾部，两标识分别向中间归拢；

2.首先从序列末尾开始找小于哨兵的元素，找到元素和低位指针所指元素进行交换；

3.然后再从左向中找大于哨兵的元素然后交换高位指针所指向的元素；

4.循环以上的步骤，直到两个指针标识碰头完成一次排序；

5.然后再递归，被分开的子序列进行同样的操作。直到子序列中只剩下少于两个元素，停止递归，完成排序。

（2）实例：

（3）优缺点

优点：当基准选取的比较合适的时候，算法的效率比较可观；

缺点：当序列基本有序，基准选取不当，算法的性能会恶化到O（n*n）;

优化：（三数取中+插排+聚集相等元素+尾递归）

　　循环过程优化

　　1）当待排序序列的长度分割到一定大小的时候，使用插入排序（适合序列大多有序）；

　　2）在一次分割结束后，可以把与key相等的元素聚在一位，继续下次分割时，不用再对key相等元素进行分割（针对序列有大量重复元素的的情况）

　　3）尾递归的优化，当基准不合适，分割的两个子序列就会极不平衡，递归的深度就会很大。采用当递归深度很大的时候采用 

　　基准点优化

　　1）采用三数取中进行优化（取首尾元素和中间元素三个数的中位数）

　　2）采用随机坐标选取随机的基准

（4）性质

（5）Java代码实现

package sorts;

public class 快速排序 {
    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        quick(a);
        for(int i=0; i<a.length;i++){
            System.out.println(a[i]);
        }
    }
    
    private static void quick(int[] a2) {
        //查看数组是否为空
        if(a2.length>1){
            _quickSort(a2,0,a2.length-1);
        }
    }
    //递归对子序列进行排序
    private static void _quickSort(int[] list, int low, int high) {
        if(low<high){
            int middle = getMiddle(list,low,high);
　　　　　　　　// 比较左半边
            _quickSort(list,low,middle-1);
　　　　　　　　// 比较右半边
            _quickSort(list,middle+1,high);
        }
    }
　　// 获取碰撞点也就是中间点
    private static int getMiddle(int[] list, int low, int high) {
　　　　　　// 默认第一个值为基准点
        int tmp = list[low];
　　　　　　// 从传入序列末尾开始查询，找到小于基准点的元素
        while(low<high){
            while(low<high && list[high]>=tmp){
                high--;
            }
　　　　　　　　// 找到小于基准点的元素，把该元素放到基准点的当前位置
            list[low] = list[high];
　　　　　　　　// 从传入序列开始位置向右寻找大于基准点的元素
            while(low<high && list[low]<=tmp){
                low++;
            }
　　　　　　　　// 找到大于基准点的元素，把该元素放到基准点的位置
            list[high]=list[low];
        }
　　　　　　// 返回基准点元素的最后位置，该位置就是最终序列的分割点
        list[low]=tmp;
        return low;
    }
    
}

 1.直接插入排序

（1）基本思想：把要进行排序的元素插入到有序的序列中，

1.首先从序列头部开始（第二个元素）作为待插入元素，

2.然后从后向前依次和该元素前面的序列中的元素进行比较，找到第一个小于（大于）待插入元素的位置；

3.用较大（较小）的那个元素覆盖待插入元素，然后再进行比较只要比待插入元素大的元素都要向后移动；

3.找到等于或者小于待插入元素的位置后停止该轮的内部循环；外循环整个2至n之间的元素；

（2）实例

（3）特点

（4）性质

（5）java代码实现

package sorts;public class 直接插入排序 {

public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        for(int i=0;i<insertSort(a).length;i++){
            System.out.println(a[i]);
        }
    }

    private static int[] insertSort(int[] a) {
        if(a == null || a.length<2){
            return a;
        }
        int temp = 0;
        for(int i=1; i<a.length; i++){
　　　　　　　　int j=i-1;
　　　　　　　　temp=a[i];

 　　　　　　　　//移动待插入元素前 比其大的元素到后一个元素的位置；

　　　　　　　　for(;j>=0&&temp<a[j];j--){  a[j+1]=a[j]; }
　　　　　　　　//插入元素到其前面的位置
　　　　　　　a[j+1]=temp;
            }
        }
        return a;
    }
}

 2.折半插入排序

（1）基本思想：和直接插入排序的不同在于找到插入位置时，使用的折半查找的方法；

（2）例子

（3）性质

（4）特点

（5）Java实现

package sorts;

public class 折半插入排序 {
    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
//        int a[]={13,27,38,49,49,65,76,78,97};
        for(int i=0;i<insertSort(a).length;i++){
            System.out.println(a[i]);
        }
        
//        insertSort1(a,13);
    }

    private static int insertSort1(int[] a,int data) {
　　　　　　// 初始化左中右三个指针位置
        int low = 0;
        int high = a.length-1;
        int middle = high/2;
　　　　　　// 循环直到左右指针位置碰撞
        while(high>=low){
　　　　　　　　// 如果基准元素和中间指针位置元素相等，结束循环，返回该位置
            if(data==a[middle]){
                break;
            }
　　　　　　　　// 如果基准元素在右半边范围，更新左指针为中间指针位置加一
            if(data > a[middle]){
                low = middle+1;
                middle = (low+high)/2;
            }
　　　　　　　　// 如果基准为元素在左半边范围，更新右指针为中间指针位置减一
            if(data<a[middle]){
                high = middle-1;
                middle = (low+high)/2;
            }
        }
        return middle;
    }

    private static int[] insertSort(int[] a) {
        if(a == null || a.length<2){
            return a;
        }
        int temp = 0;
        int index = 0;
        for(int i=1; i<a.length; i++){
            //从第二个元素a[1]开始遍历元素；
            temp = a[i];
            index = getBinaryIndex(0,i,a[i], a);
            //从序列头开始遍历依次移动i-low个元素；当a[low]=a[i-1]时说明a[i]为最大值，放在有序子序列的末尾；
            for(int j = i-1; j>=index; j--){
                a[j+1] = a[j];
                }
            a[index] = temp;
            }
        return a;
    }

    private static int getBinaryIndex(int low, int high,int data,int[] a) {
        int middle = high;
        //利用折半查找，找到a[i]应在位置返回low指针，应为low是肯定小于a[i]的位置，
        while(low<=high){
            middle=(low+high)/2;
            if(data == a[middle]){
                break;
            }
            if(data > a[middle]){
                low = middle+1;
            }
            if(data<a[middle]){
                high = middle-1;
            }
        }
        return low;
    }
}

 3.希尔排序

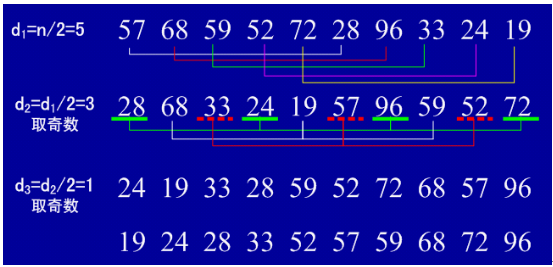
（1）基本思想：算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d，

然后比较i和i+d所对应的的元素的大小，如果后者小于前者，就要交换 这两个元素；逐渐增大i到d结束；这是整个内循环的过程，循环结束对应的i和i+d位置的元素都是i<i+d；

接下来，比较开始缩小d的范围到d/2，循环上一个步骤；

当d逐渐缩小时，i位置的元素会和多个元素比较（i+d，i+2d，i+3d。。。。）；

（2）例子

（3）性质

（4）特点

（5）Java实现

package sorts;

public class 希尔排序 {
    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        for(int i=0;i<shellSort(a).length;i++){
            System.out.println(a[i]);
        }
    }

    private static int[] shellSort(int[] a) {
        double d1 = a.length;
        int temp = 0;
        while(true){
　　　　　　　　// 第一层循环，从序列的一半长度d一直循环到该长度为1，达到基准条件
            d1 = Math.ceil(d1/2);
            int d = (int)d1;
　　　　　　　　// 第二层循环，在d范围内比较其后面紧临的一个d范围元素
            for(int x=0; x<d; x++){
　　　　　　　　　　// 第三层循环，比较i和i+d元素的大小
                for(int i=x+d;i<a.length;i+=d){
                    int j=i-d;
                    temp = a[i];
　　　　　　　　　　　　// 
                    for(;j>=0&&temp<a[j];j-=d){
                        a[j+d]=a[j];
                    }
                    a[j+d]=temp;
                }
            }
　　　　　　// 基准条件 当跨域只有一个元素的时候停止比较
            if(d==1){
                break;
            }
        }
        return a;
    }
}

1.简单选择排序

(1)基本思想：和冒泡的不同是，两个算法的交换次数，冒泡排序是每次比较后条件成立都会进行交换，而选择排序只是重新记录了较小元素的下标；待循环结束；

直接替换a[i]的值；

（2）例子

（3）性质

（4）特点

（5）java实现

package sorts;

public class 简单选择排序 {
    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        changeSort(a);
    }

    private static void changeSort(int[] a) {
        int point;
        for(int i=0; i<a.length; i++){
            int temp = a[i];
            point = i;
            for(int j=i+1; j<a.length; j++){
                if(a[point]>a[j]){
                    point = j;
                }
            }
            a[i]= a[point];
            a[point] = temp;
        }
        
        for(int k=0; k<a.length; k++)
            System.out.println(a[k]);
    }
}

2.堆排序

（1）基本思想：不断构造堆，交换堆顶与末尾未排序的每一个元素，直到全部都排完。

应用到topK问题：

　　创建一个大小为k的数组，对该数组构造堆，如果是求解最大的k个数，构建的是小顶堆，反之构建的是大顶堆。

　　遍历数组中剩余的元素，依次与构建好的堆顶元素比较，比堆顶元素还要小的元素无需置换，如果堆顶元素被置换之后，需要调整堆，找到堆内最小的元素放到堆顶。

堆的定义：具有n个元素的序列（h1,h2,....,hn）,当且仅当满足（hi>h2i,hi>=2i+1）或（hi<=h2i,hi<2i+1）时；

（2）实例

（3）性质

（4）特点

（5）java实现

package sorts;

import java.util.Arrays;

public class 堆排序 {
    public static void main(String[] args) {
        int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
        heapSort(a);
    }

    private static void heapSort(int[] a) {
        int arrayLength = a.length;
        //循环建堆
        for(int i=0; i<arrayLength; i++){
            //建堆
            buildMaxHeap(a,arrayLength-1-i);
            //交换堆顶和最后一个元素
            swap(a,0,arrayLength-1-i);
            System.out.println(Arrays.toString(a));
        }
    }

    private static void buildMaxHeap(int[] data, int lastIndex) {
        //从lastIndex处节点的父节点开始
        for(int i=(lastIndex-1)/2; i>=0; i--){
            //k保存正在判断的节点
            int k=i;
            //如果当前k节点的子节点存在
            while(k*2+1<=lastIndex){
                //k节点的左子节点的索引
                int biggerIndex = 2*k+1;
                //如果biggerIndex小于lastIndex，即biggerIndex+1存在
                if(biggerIndex<lastIndex){
                    //如果右子节点的值较大
                    if(data[biggerIndex]<data[biggerIndex+1]){
                        //biggerIndex总是记录较大子节点的索引
                        biggerIndex++;
                    }
                }
                //如果k节点的值小于其较大的子节点的值
                if(data[k]<data[biggerIndex]){
                    //交换他们
                    swap(data,k,biggerIndex);
                    //奖biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值
                    //k节点的值大于其左右节点的值；
                    k=biggerIndex;
                }else{
                    break;
                }
            }
        }
    }

    private static void swap(int[] data, int i, int j) {
        int tmp = data[i];
        data[i] = data[j];
        data[j] = tmp;
    }
}

public class HeapDemo {
    public static void main(String[] args){     
        //最小堆实现从大到小排序
        int[] arrSort = {90,3,60,6,7,2,89,100,33,5};        
        MinHeap heap1 = new MinHeap(arrSort);
        for(int i = arrSort.length - 1;i > 0; i --){
            //把最小的元素移到末尾
            heap1.swap(0, i);
            //重新构造最小堆
            heap1.buildHeap(i);
        }
        //打印排序后的数组
        for(int i = 0; i < arrSort.length;i ++){
            System.out.println(arrSort[i]);
        }       
        
        //最小堆实现topK
        int[] arrTopK = {90,44,60,6,71,2,38,13,33,5};
        int k = 3;
        //创建一个大小为k的数组
        int[] data = new int[k];
        for(int i = 0; i < k; i ++){
            data[i] = arrTopK[i];
        }       
        MinHeap heap = new MinHeap(data);       
        for(int i = k; i < arrTopK.length; i ++){
            //如果大于堆顶的元素则替换顶并重新构造
            if(arrTopK[i] > heap.getRoot()) heap.setRoot(arrTopK[i]);           
        }       
        //打印最大的k个数
        for(int i = 0; i < k; i ++){
            System.out.println(data[i]);
        }
    }

    //最小堆类
    static class MinHeap{
        private int[] data;
        public MinHeap(int[] data){
            this.data = data;
            buildHeap(data.length);
        }

        public void buildHeap(int heapSize){
            for(int i = heapSize / 2 - 1; i >= 0;i --){
                heapify(i, heapSize);
            }
        }

        public void heapify(int index,int heapSize){
            int right = right(index);

            int left = left(index);

            int min = index;

            if(right < heapSize && data[right] < data[min]) min = right;

            if(left < heapSize && data[left] < data[min]) min = left;

            if(min == index) return;

            swap(index,min);

            heapify(min,heapSize);
        }

        private int right(int index){
            //右儿子的下标
            return (index + 1) << 1;
        }

        private int left(int index){
            //左儿子的下标
            return ((index + 1) << 1) - 1;
        }

        public void swap(int index1,int index2){
            int tmp = data[index1];
            data[index1] = data[index2];
            data[index2] = tmp;
        }

        public int getRoot(){
            return data[0];
        }

        public void setRoot(int root){
            data[0] = root;
            heapify(0, data.length);
        }
    }
}

1.归并排序

（1）基本思想：

将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。

然后再把有序子序列合并为整体有序序列。

（2）实例

（3）性质

（4）特点

（5）java实现

package sorts;

import java.util.Arrays;

import org.junit.Test;

public class 归并排序 {
    static int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
    public static void 归并排序1(){
        sort(a,0,a.length-1);
        for(int i=0; i<a.length; i++){
            System.out.println(a[i]);
        }
    }
    
    @Test
    public void ru(){
        this.归并排序1();
    }
    private static void sort(int[] data, int left, int right) {
        if(left<right){
            //找出中间索引
            int center = (left+right)/2;
            //对左边数组进行递归
            sort(data,left,center);
            //对右边数组进行递归
            sort(data,center+1,right);
            merge(data,left,center,right);
        }
    }
    private static void merge(int[] data, int left, int center, int right) {
        int [] tmpArr = new int[data.length];
        int mid = center + 1;
        //third记录中间数组的索引
        int third = left;
        int tmp = left;
        while(left<=center&&mid<=right){
            //从两个数组中取出最小的放入中间数组
            if(data[left]<=data[mid]){
                tmpArr[third++]=data[left++];
            }else{
                tmpArr[third++]=data[mid++];
            }
        }
        //剩余部分依次放入中间数组
        while(mid<=right){
            tmpArr[third++]=data[mid++];
        }
        while(left<=center){
            tmpArr[third++]=data[left++];
        }
        //将中间数组中的内容复制回原数组
        while(tmp<=right){
            data[tmp]=tmpArr[tmp++];
        }
        System.out.println(Arrays.toString(data));
    }
}

 2.基数排序

（1）基本思想：将所有有待比较的数值（正整数）统一为同样的数位长度，数位较短的说在前面补零，然后，从最低位开始进行一次排序；

这样从最低位排序到最高位排序完成以后，数列就变成一个有序的序列；

（2）实例：

（3）性质：

（4）特点：

（5）java实现

package sorts;

import java.util.ArrayList;
import java.util.List;

import org.junit.Test;

public class 基数排序 {
    static int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,101,56,17,18,23,34,15,35,25,53,51};
    
    @Test
    public  void 基数排序1(){
        sort(a);
        for(int i=0; i<a.length; i++){
            System.out.println(a[i]);
        }
    }
    
    private static void sort(int[] array) {

        //首先确定排序的趟数
        int max=array[0];
        for(int i=0; i<array.length; i++){
            if(array[i]>max){
                max=array[i];
            }
        }
        
        int time=0;
        //判断位数
        while(max>0){
            max/=10;
            time++;
        }
        
        //建立10个队列
        List<ArrayList> queue = new ArrayList<ArrayList>();
        for(int i=0; i<10; i++){
            ArrayList<Integer> queue1 = new ArrayList<Integer>();
            queue.add(queue1);
        }
        
        //进行time次分配和收集
        for(int i=0; i<time;i++){
            
            //分配数组元素
            for(int j=0;j<array.length; j++){
                //得到数字的第time+1位数
                int x=array[j]%(int)Math.pow(10, i+1)/(int)Math.pow(10, i);
                ArrayList<Integer> queue2 = queue.get(x);
                queue2.add(array[j]);
                queue.set(x, queue2);
            }
            
            int count = 0;//元素计数器
            
            //收集队列元素
            for(int k=0; k<10; k++){
                while(queue.get(k).size()>0){
                    ArrayList<Integer> queue3 = queue.get(k);
                    array[count]=queue3.get(0);
                    queue3.remove(0);
                count++;
                }
            }
        }
    }
}