基本思想:
在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数当中再找最小(或者最大)的与第2个位置的数交换,依次类推,直到第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。
简单选择排序的示例:
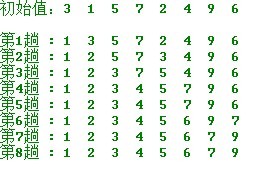
操作方法:
第一趟,从n 个记录中找出关键码最小的记录与第一个记录交换;
第二趟,从第二个记录开始的n-1 个记录中再选出关键码最小的记录与第二个记录交换;
以此类推.....
第i 趟,则从第i 个记录开始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换,
直到整个序列按关键码有序。
算法实现:
void print(int a[], int n ,int i){
cout<<"第"<<i+1 <<"趟 : ";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
/**
* 数组的最小值
*
* @return int 数组的键值
*/
int SelectMinKey(int a[], int n, int i)
{
int k = i;
for(int j=i+1 ;j< n; ++j) {
if(a[k] > a[j]) k = j;
}
return k;
}
/**
* 选择排序
*
*/
void selectSort(int a[], int n){
int key, tmp;
for(int i = 0; i< n; ++i) {
key = SelectMinKey(a, n,i); //选择最小的元素 递归
if(key != i){
tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素与第i位置元素互换
}
print(a, n , i);
}
}
int main(){
int a[8] = {3,1,5,7,2,4,9,6};
cout<<"初始值:";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl<<endl;
selectSort(a, 8);
print(a,8,8);
}
简单选择排序的改进——二元选择排序
简单选择排序,每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序,最多只需进行[n/2]趟循环即可。具体实现如下
void SelectSort(int r[],int n) {
02. int i ,j , min ,max, tmp;
03. for (i=1 ;i <= n/2;i++) {
04. // 做不超过n/2趟选择排序
05. min = i; max = i ; //分别记录最大和最小关键字记录位置
06. for (j= i+1; j<= n-i; j++) {
07. if (r[j] > r[max]) {
08. max = j ; continue ; //continue不可少,否则可能会漏掉一些数据,min的值偏大
09. }
10. if (r[j]< r[min]) {
11. min = j ;
12. }
13. }
14. //该交换操作还可分情况讨论以提高效率
15. tmp = r[i-1]; r[i-1] = r[min]; r[min] = tmp;
16. tmp = r[n-i]; r[n-i] = r[max]; r[max] = tmp;
17.
18. }
19.}