12.7 61. 确定两个字符串是否接近
如果可以使用以下操作从一个字符串得到另一个字符串,则认为两个字符串 接近 :
操作 1:交换任意两个 现有 字符。
例如,abcde -> aecdb
操作 2:将一个 现有 字符的每次出现转换为另一个 现有 字符,并对另一个字符执行相同的操作。
例如,aacabb -> bbcbaa(所有 a 转化为 b ,而所有的 b 转换为 a )
你可以根据需要对任意一个字符串多次使用这两种操作。
给你两个字符串,word1 和 word2 。如果 word1 和 word2 接近 ,就返回 true ;否则,返回 false 。
输入:word1 = "abc", word2 = "bca"
输出:true
解释:2 次操作从 word1 获得 word2 。
执行操作 1:"abc" -> "acb"
执行操作 1:"acb" -> "bca"
输入:word1 = "a", word2 = "aa"
输出:false
解释:不管执行多少次操作,都无法从 word1 得到 word2 ,反之亦然。
输入:word1 = "cabbba", word2 = "abbccc"
输出:true
解释:3 次操作从 word1 获得 word2 。
执行操作 1:"cabbba" -> "caabbb"
执行操作 2:"caabbb" -> "baaccc"
执行操作 2:"baaccc" -> "abbccc"
输入:word1 = "cabbba", word2 = "aabbss"
输出:false
解释:不管执行多少次操作,都无法从 word1 得到 word2 ,反之亦然。
思路
用collection.Counter来得到字典列表,对于操作一来说,只要字典列表不变就一定会互换。对于操作二,相同数目的字典列表就可以互换。
我的解
class Solution:
def closeStrings(self, word1: str, word2: str) -> bool:
from collections import Counter
c_1 = Counter(word1)
c_2 = Counter(word2)
s_1 = set()
l_1 = list()
s_2 = set()
l_2 = list()
for k,v in c_1.items():
s_1.add(k)
l_1.append(v)
li_1 = sorted(l_1)
for k,v in c_2.items():
s_2.add(k)
l_2.append(v)
li_2 = sorted(l_2)
if s_1 == s_2 and li_1 == li_2:
return True
return False
12.8 62. 不用加减乘除做加法
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
输入: a = 1, b = 1
输出: 2
最优解思路
设两数字的二进制形式a,b,其求和s = a + b, a(i)表示a的二进制第i位,则分为以下四种情况:
| a(i) | b(i) | 无进位和n(i) | 进位和c(i+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
观察发现,无进位和 与 异或运算 规律相同,进位 和 与运算 规律相同(并需左移一位)。
- n=a⊕b 非进位和 异或运算
- c=a&b<<1 进位:与运算 + 左移一位
(和 s )==(非进位和 n )++(进位 c )。即可将 s = a + b转化为:s=a+b⇒s=n+c
最优解
class Solution:
def add(self, a: int, b: int) -> int:
x = 0xffffffff
a, b = a & x, b & x
while b != 0:
a, b = (a ^ b), (a & b) << 1 & x
return a if a <= 0x7fffffff else ~(a ^ x)
总结
不能用加减乘除的时候想一下计算机内部完成四则运算是如何算的。
12.9 63. 元素和小于等于预知的正方形最大边长
给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。
请你返回元素总和小于或等于阈值的正方形区域的最大边长;如果没有这样的正方形区域,则返回 0 。
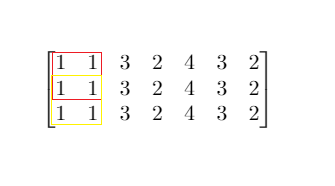
输入:mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出:2
解释:总和小于 4 的正方形的最大边长为 2,如图所示。
最优解
class Solution:
def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
m, n = len(mat), len(mat[0])
P = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + mat[i - 1][j - 1]
def getRect(x1, y1, x2, y2):
return P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]
l, r, ans = 1, min(m, n), 0
while l <= r:
mid = (l + r) // 2
find = any(getRect(i, j, i + mid - 1, j + mid - 1) <= threshold for i in range(1, m - mid + 2) for j in range(1, n - mid + 2))
if find:
ans = mid
l = mid + 1
else:
r = mid - 1
return ans
最优解总结
前缀和数组的算法,数组 P 可以帮助我们在 O(1)O(1) 的时间内求出任意一个矩形区域的元素之和。具体地,设我们需要求和的矩形区域的左上角为 (x1, y1),右下角为 (x2, y2),则该矩形区域的元素之和可以表示为:
sum = A[x1..x2][y1..y2]
= P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]
那么如何得到数组 P 呢?我们按照行优先的顺序依次计算数组 P 中的每个元素,即当我们在计算 P[i][j] 时,数组 P 的前 i - 1 行,以及第 i 行的前 j - 1 个元素都已经计算完成。此时我们可以考虑 (i, j) 这个 1 * 1 的矩形区域,根据上面的等式,有:
P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + A[i][j]
- 掌握前缀和数组的计算思想
- 如果想到遍历来算的,优先想二分法是否可以解决。
12.11 64. 二叉树剪枝
给定二叉树根结点 root ,此外树的每个结点的值要么是 0,要么是 1。
返回移除了所有不包含 1 的子树的原二叉树。
( 节点 X 的子树为 X 本身,以及所有 X 的后代。)
示例1:
输入: [1,null,0,0,1]
输出: [1,null,0,null,1]
解释:
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。
示例3:
输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]

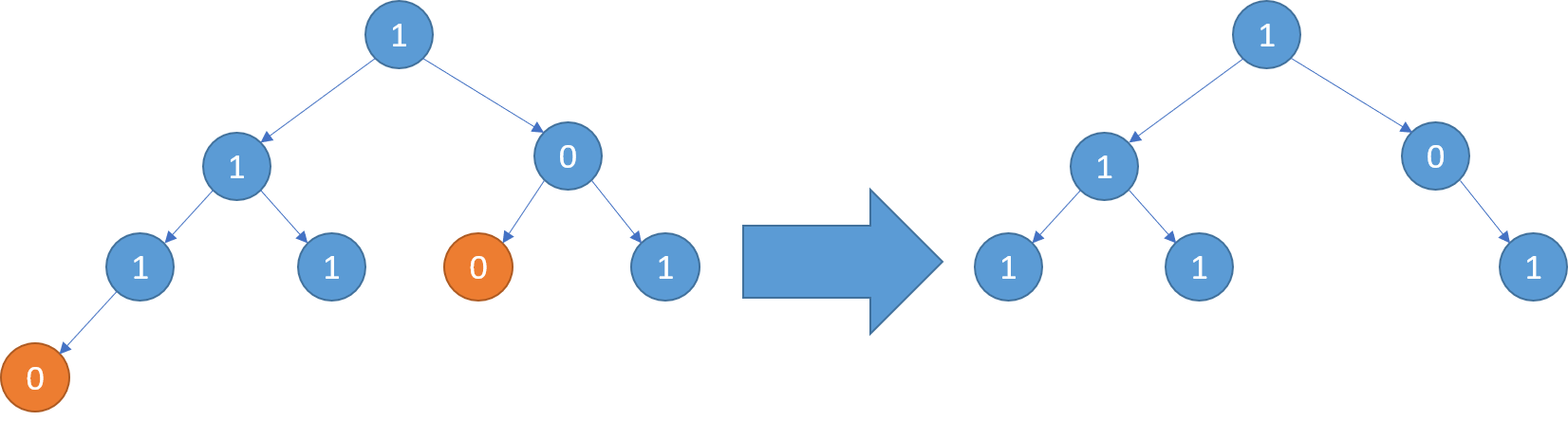
思路
递归左右节点,一直为null时,就删除。有一个不为null就不修理此节点。
最优解
class Solution(object):
def pruneTree(self, root):
def containsOne(node):
if not node: return False
# 左节点递归
a1 = containsOne(node.left)
# 右节点递归
a2 = containsOne(node.right)
# 若有一个为1,则该节点为1
if not a1: node.left = None
if not a2: node.right = None
return node.val == 1 or a1 or a2
# 过滤函数,每个节点都如此操作
return root if containsOne(root) else None
最优解总结
每个点递归,结束条件是节点中不含1.
12.12 65. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下二叉树
3
/
9 20
/
15 7
最优解思路
前序遍历的第一个节点是根节点,只要找到根节点在中序遍历中的位置,在根节点之前被访问的节点都位于左子树,在根节点之后被访问的节点都位于右子树,由此可知左子树和右子树分别有多少个节点。
由于树中的节点数量与遍历方式无关,通过中序遍历得知左子树和右子树的节点数量之后,可以根据节点数量得到前序遍历中的左子树和右子树的分界,因此可以进一步得到左子树和右子树各自的前序遍历和中序遍历,可以通过递归的方式,重建左子树和右子树,然后重建整个二叉树。
最优解
inorder = [9,3,15,20,7class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
def recur(root, left, right):
if left > right: return # 递归终止
node = TreeNode(preorder[root]) # 建立根节点
i = dic[preorder[root]] # 划分根节点、左子树、右子树
node.left = recur(root + 1, left, i - 1) # 开启左子树递归
node.right = recur(i - left + root + 1, i + 1, right) # 开启右子树递归
return node # 回溯返回根节点
dic, preorder = {}, preorder
for i in range(len(inorder)):
dic[inorder[i]] = i
return recur(0, 0, len(inorder) - 1)
总结
最优解大概思路是清晰的,在递归中,右子树根节点坐标要注意定义,“i - left + root + 1”,其实就是右子树根节点=(中序根节点坐标-中序左边界)+先序根节点坐标+1,其中括号内=左子树长度。这一块理解有难度。重建二叉树
//利用原理,先序遍历的第一个节点就是根。在中序遍历中通过根 区分哪些是左子树的,哪些是右子树的
//左右子树,递归
HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
int[] preorder;//保留的先序遍历
public TreeNode buildTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
for (int i = 0; i < preorder.length; i++) {
map.put(inorder[i], i);
}
return recursive(0,0,inorder.length-1);
}
/**
* @param pre_root_idx 先序遍历的索引
* @param in_left_idx 中序遍历的索引
* @param in_right_idx 中序遍历的索引
*/
public TreeNode recursive(int pre_root_idx, int in_left_idx, int in_right_idx) {
//相等就是自己
if (in_left_idx > in_right_idx) {
return null;
}
//root_idx是在先序里面的
TreeNode root = new TreeNode(preorder[pre_root_idx]);
// 有了先序的,再根据先序的,在中序中获 当前根的索引
int idx = map.get(preorder[pre_root_idx]);
//左子树的根节点就是 左子树的(前序遍历)第一个,就是+1,左边边界就是left,右边边界是中间区分的idx-1
root.left = recursive(pre_root_idx + 1, in_left_idx, idx - 1);
//由根节点在中序遍历的idx 区分成2段,idx 就是根
//右子树的根,就是右子树(前序遍历)的第一个,就是当前根节点 加上左子树的数量
// pre_root_idx 当前的根 左子树的长度 = 左子树的左边-右边 (idx-1 - in_left_idx +1) 。最后+1就是右子树的根了
root.right = recursive(pre_root_idx + (idx-1 - in_left_idx +1) + 1, idx + 1, in_right_idx);
return root;