9.28 16. 复数乘法
给定两个表示复数的字符串。
返回表示它们乘积的字符串。注意,根据定义 i2 = -1 。
输入: "1+1i", "1+1i"
输出: "0+2i"
解释: (1 + i) * (1 + i) = 1 + i2 + 2 * i = 2i ,你需要将它转换为 0+2i 的形式。
输入: "1+-1i", "1+-1i"
输出: "0+-2i"
解释: (1 - i) * (1 - i) = 1 + i2 - 2 * i = -2i ,你需要将它转换为 0+-2i 的形式。
注意:
输入字符串不包含额外的空格。
输入字符串将以 a+bi 的形式给出,其中整数 a 和 b 的范围均在 [-100, 100] 之间。输出也应当符合这种形式。
我的解
class Solution:
@classmethod
def complexNumberMultiply(self, a: str, b: str) -> str:
a1,a2 = a.split('+')
b1,b2 = b.split('+')
new_a2 = a2[:-1]
new_b2 = b2[:-1]
constant = int(a1)*int(b1)
sum_i = int(a1) * int(new_b2) + int(b1) * int(new_a2)
new_sum_i = "+" + str(sum_i)
i = int(new_a2) * int(new_b2)
return str(constant-i) + str(new_sum_i)+"i"
9.29 17. 将矩阵按对角线排序
给你一个 m * n 的整数矩阵 mat ,请你将同一条对角线上的元素(从左上到右下)按升序排序后,返回排好序的矩阵。
示例 1:
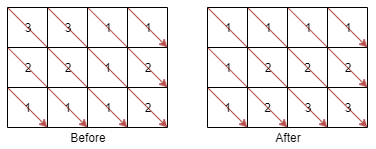
输入:mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出:[[1,1,1,1],[1,2,2,2],[1,2,3,3]]
思路
设有m行n列,取对角线元素组成一个新数组排序好写回去,遍历的时候要考虑行数和列数的关系。
最优解
解法一:迭代器
如下所示,用d = 行数-列数获取行列关系
| 0 | -1 | -2 | -3 |
|---|---|---|---|
| 1 | 0 | -1 | -2 |
| 2 | 1 | 0 | -1 |
class Solution:
@classmethod
def diagonalSort(self, mat: list) -> list:
import collections
import itertools
m, n, d = len(mat), len(mat[0]), collections.defaultdict(list)
for i, j in itertools.product(range(m), range(n)):
d[i - j].append(mat[i][j])
d = {k: iter(sorted(v)) for k, v in d.items()}
for i,j in itertools.product(range(m),range(n)):
mat[i][j] = next(d[i-j])
return mat
体会一下
- 构造i-j的原因,很巧妙的构造。
- 使用itertools.product来代替多重for循环。
- iter函数来实现对象的可迭代。
解法二:迭代指针
function diagonalSort(mat: number[][]): number[][] {
const [m, n] = [mat.length, mat[0].length]
const d: { [_: number]: number[] } = {}
mat.forEach((v, i) => v.forEach((a, j) => {
if (!d[i - j]) {
d[i - j] = []
}
d[i - j].push(a)
}))
const it: { [_: number]: number } = {}
for (const k in d) {
d[k].sort((a, b) => a - b)
it[k] = 0
}
mat.forEach((v, i) => v.forEach((_, j) => {
mat[i][j] = d[i - j][it[i - j]++]
}))
return mat
};
解法三:堆
class Solution:
def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:
m, n = len(mat), len(mat[0])
d = [[] for _ in range(m + n - 1)]
for i, j in itertools.product(range(m), range(n)):
heapq.heappush(d[i - j], mat[i][j])
for i, j in itertools.product(range(m), range(n)):
mat[i][j] = heapq.heappop(d[i - j])
return mat
10.4 18. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
最优解
动态规划
class Solution:
@classmethod
def maxSubArray(self, nums: list) -> int:
pre = 0
max_ans = nums[0]
for i in nums:
pre = max(pre + i, i)
max_ans = max(max_ans,pre)
return max_ans
此题设只要求最大值,争取一次遍历求解,后一次和前一次比较,pre一直取的是被加数的最大值,也包含了遍历过的列表的信息,max_ans则会比较并存储已经存储的最大值。
max函数既可以比较,也存储了信息,之前也有做到,需要加深记忆。
动态规划的思想,要从最小的延伸到最大的通用算法。

10.9 19. 最小除数
给你一个整数数组 nums 和一个正整数 threshold ,你需要选择一个正整数作为除数,然后将数组里每个数都除以它,并对除法结果求和。
请你找出能够使上述结果小于等于阈值 threshold 的除数中 最小 的那个。
每个数除以除数后都向上取整,比方说 7/3 = 3 , 10/2 = 5 。
题目保证一定有解。
输入:nums = [1,2,5,9], threshold = 6
输出:5
解释:如果除数为 1 ,我们可以得到和为 17 (1+2+5+9)。
如果除数为 4 ,我们可以得到和为 7 (1+1+2+3) 。如果除数为 5 ,和为 5 (1+1+1+2)。
输入:nums = [2,3,5,7,11], threshold = 11
输出:3
思路
遍历求和,直到小于阈值。
我的解
class Solution:
@classmethod
def smallestDivisor(self, nums: list, threshold: int) -> int:
import math
sum = 0
div = 1
while sum == 0:
for i in nums:
sum += math.ceil(i / div)
if sum > threshold:
div += 1
sum = 0
break
else:
return div
最优解
from typing import List
class Solution:
def smallestDivisor(self, nums: List[int], threshold: int) -> int:
left = 1
right = max(nums)
while left < right:
mid = (left + right) >> 1
if sum([(num + mid - 1) // mid for num in nums]) > threshold:
left = mid + 1
else:
right = mid
return left
总结
除数的最小值为1,最大值是数组中最大的数,用二分法找到符合要求最大的数。
10.11 20. 丑数
请你帮忙设计一个程序,用来找出第 n 个丑数。
丑数是可以被 a 或 b 或 c 整除的 正整数。
输入:n = 3, a = 2, b = 3, c = 5
输出:4
解释:丑数序列为 2, 3, 4, 5, 6, 8, 9, 10... 其中第 3 个是 4。
输入:n = 4, a = 2, b = 3, c = 4
输出:6
解释:丑数序列为 2, 3, 4, 6, 8, 9, 10, 12... 其中第 4 个是 6。
输入:n = 5, a = 2, b = 11, c = 13
输出:10
解释:丑数序列为 2, 4, 6, 8, 10, 11, 12, 13... 其中第 5 个是 10。
最优解
class Solution:
@classmethod
def nthUglyNumber(self, n, a, b, c):
from math import gcd
def lcm(a,b,c):
x = (a*b)/gcd(a,b)
return (x*c)/gcd(x,c)
"""
计算有多少个丑数小于等于x
+ x整除a,b,c(ab算了2次,bc算了2次,ac算了2次,abc算了3次) -整除ab,bc,ac最小公倍数(abc算了3次) +整除abc最小公倍数 即为所求
"""
def uglynum(x):
return x // a + x // b + x // c - x // (a * b // gcd(a, b)) - x // (a * c // gcd(a, c)) - x // (
b * c // gcd(b, c)) + x // lcm(a, b, c)
'''
二分搜索,注意只要uglynum(mid)<n left就=mid+1 所以最后得到的left就是所求
例如测试用例2中 a=2,b=3,c=4
括号中为丑数 1,(2),(3),(4),5,(6),7,(8)
小于等于它们的丑数个数分别为 0, 1 , 2 , 3 ,3, 4, 4, 5
若n==4
如果uglynum(mid)<4 则left一定能直接取到6而不是7
'''
left = 1
right = n * min(a, b, c)
while left < right:
mid = (left + right) // 2
if uglynum(mid) < n:
left = mid + 1
else:
right = mid
return left
总结
构建一个函数,使得输入一个值,返回有多少个丑数小于等于他。左边界为1,右边界至少为n*min(a,b,c)。然后根据二分法再去寻找。用二分法来保证如果有相同的数,取到的是第一个。比如uglynum(5)=3<4,left=6,不可能大于6。uglynum(7)=4,right会变,left不会变。所以永远不会大于最小的丑数6
两个小技巧求最小公倍数和最大公约数
// 最小公倍数
private long lcm(long a, long b) {
return a * b / gcd(a, b);
}
// 最大公因数
private long gcd(long a, long b) {
if (a == 0) return b;
return gcd(b % a, a);
}