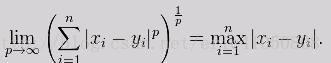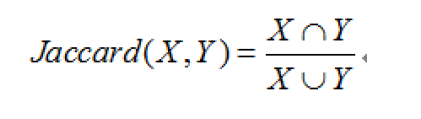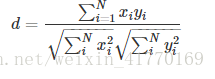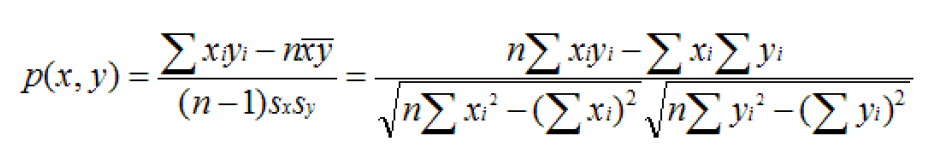有时候,我们需要度量两个向量之间的距离来决定他们的归属。
接下来列举一些常用的距离度量方法
1、欧氏距离
2、马氏距离
3、曼哈顿距离
4、闵可夫斯基距离
5、汉明距离
6、杰卡德相关系数
7、余弦相似度
8、切比雪夫距离
9、皮尔逊相关系数
1、欧氏距离:也叫欧几里得距离
两点之间或多点之间的距离表示法
![]()
二维空间的公式:
![]()
![]()
其中,
![]() 为点
为点![]() 与点
与点![]() 之间的欧氏距离;
之间的欧氏距离;![]() 为点
为点![]() 到原点的欧氏距离。
到原点的欧氏距离。
n维空间的公式:
![]()
其实就是应用勾股定理计算两个点的直线距离,它会受指标不同单位刻度影响,所以,在使用前一般要先标准化,距离越大,个体间差异越大
改进方法1:
标准化欧氏距离:针对各分量分布不一致,将各分量都标准化到均值,方差相等
标准化后值:(标准化前的值-分量的均值)/分量标准差
改进方法2:
2、马氏距离(Mahalanobis):表示点与分布之间的距离,考虑到各种特性之间的联系,且尺度无关。
方差:方差是标准差的平方,标准差的意义是数据集中各个点到均值点距离的平均值,描述的是数据的离散程度。
协方差:标准差和方差是描述一维数据的,当存在多维数据时,需要知道每个维度之间的变量中间是否关联。协方差是衡量多维数据集中,变量之间相关性的统计量。比如:一个人的身高和体重的关系,就需要用协方差来衡量。
协方差矩阵:当变量超过两个,就需要使用协方差矩阵来衡量相关性。ui是第i个元素的期望值,μi=E(Xi)。协方差矩阵的第i,j项(第i,j项是一个协方差)被定义为如下形式:
![]()
马氏距离:马氏距离(Mahalanobis)是由马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。与欧氏距离不同的是它考虑到各种特性之间的联系。对于均值为μ=(μ1,μ2,μ3,...,μp)T,协方差为Σ的多变量向量x=(x1,x2,x3,...,xp)T,
,马氏距离为sqrt((x-μ)Σ^(-1)(x-μ))
![]()
如果S^(-1)是单位阵的时候,马氏距离简化为欧氏距离.
3、曼哈顿距离(Manhattan)
表示两个点在标准坐标系上的绝对轴距之和
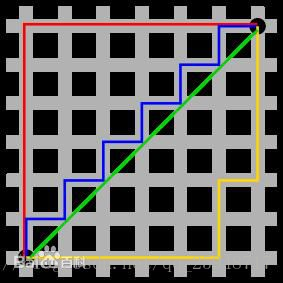
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即d(i,j)=|xi-xj|+|yi-yj|。
4、闵可夫斯基距离
闵可夫斯基距离(Minkowski distance)是衡量数值点之间距离的一种非常常见的方法,假设数值点 P 和 Q 坐标如下:
那么,闵可夫斯基距离定义为:
当 p 趋近于无穷大时,闵可夫斯基距离转化成切比雪夫距离(Chebyshev distance):
5、汉明距离(Hammi)
汉明距离是一个概念,它表示两个(相同长度)字对应位不同的数量
比如:1011101 与 1001001 之间的汉明距离是 2
6、杰卡德相关系数
杰卡德相似系数是衡量两个集合相似度的一种指标
主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。
7、余弦相似度(cosine similarity)
用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。
cosine distance = 1 - cosine similarity
cos(seta) = (a^2+b^2-c^2)/(2ab)
或
cos(seta) =(a*b)/(||a||x||b||)
或
(x1,y1)*(x2,y2)/sqrt(x1^2+y1^2)xsqrt(x2^2+y2^2)
==
(x1x2,+y1y2)/sqrt(x1^2+y1^2)xsqrt(x2^2+y2^2)
余弦相似度的夹角相似度度量不会受指标刻度影响,余弦值在区间【-1,1】,值越大,越相似。
8、切比雪夫距离(Chebyshev distance)
切比雪夫距离(Chebyshev distance)或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。
设平面空间内存在两点,它们的坐标为(x1,y1),(x2,y2)
则dis=max(|x1−x2|,|y1−y2|)
即两点横纵坐标差的最大值
9、皮尔逊相关系数
如果比较X与Y的Jaccard相似系数,只比较xn和yn中相同的个数,公式如下:
如集合A={1,2,3,4};B={3,4,5,6};
那么他们的J(X,Y)=1{3,4}/1{1,2,3,4,5,6}=1/3;
相关系数的分类:
0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关