竞赛地址:http://www.pkbigdata.com/common/cmpt/%E7%94%A8%E6%88%B7%E8%B4%B7%E6%AC%BE%E9%A3%8E%E9%99%A9%E9%A2%84%E6%B5%8B_%E8%B5%9B%E4%BD%93%E4%B8%8E%E6%95%B0%E6%8D%AE.html
数据探索:
比赛一共提供五张表,分别是:
训练数据:用户基本属性,银行流水记录,用户浏览行为,信用卡账单记录,放款时间,是否逾期
测试数据:用户基本属性,银行流水记录,用户浏览行为,信用卡账单记录,放款时间,用户ID 最后预测这些用户ID是否会逾期
一、用户基本属性
数据一共55596条,包括六个字段(ID,性别,职业,教育程度,婚姻状况,户口类型)可以试着探索各个属性与是否逾期的关系
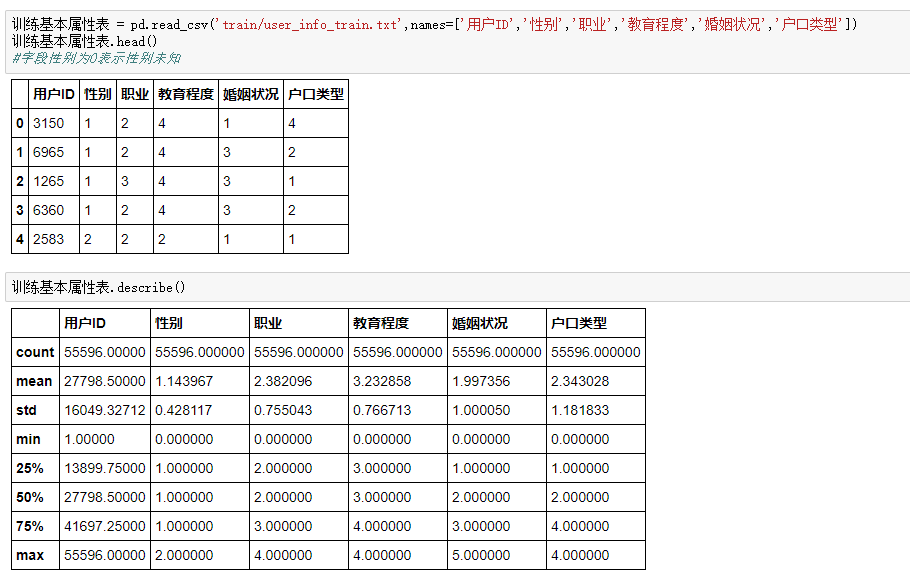
五个属性的数量分布
fig,ax = plt.subplots(2,3)
fig.set_size_inches(20,12)
p = sns.color_palette()
ax[0][0].bar(训练基本属性表.iloc[:,1].value_counts().index,训练基本属性表.iloc[:,1].value_counts(),color = p[0])
ax[0][0].set_xlabel(训练基本属性表.iloc[:,1].value_counts().name)
ax[0][1].bar(训练基本属性表.iloc[:,2].value_counts().index,训练基本属性表.iloc[:,2].value_counts(),color = p[1])
ax[0][1].set_xlabel(训练基本属性表.iloc[:,2].value_counts().name)
ax[0][2].bar(训练基本属性表.iloc[:,3].value_counts().index,训练基本属性表.iloc[:,3].value_counts(),color = p[2])
ax[0][2].set_xlabel(训练基本属性表.iloc[:,3].value_counts().name)
ax[1][0].bar(训练基本属性表.iloc[:,4].value_counts().index,训练基本属性表.iloc[:,4].value_counts(),color = p[3])
ax[0][0].set_xlabel(训练基本属性表.iloc[:,1].value_counts().name)
ax[1][0].set_xlabel(训练基本属性表.iloc[:,4].value_counts().name)
ax[1][1].bar(训练基本属性表.iloc[:,5].value_counts().index,训练基本属性表.iloc[:,5].value_counts(),color = p[4])
ax[1][1].set_xlabel(训练基本属性表.iloc[:,5].value_counts().name
性别中1的数量明显更多,职业中2的职业也更多,受教育程度更多是3,4,婚姻状况更多是1,3,户口类型较为平均
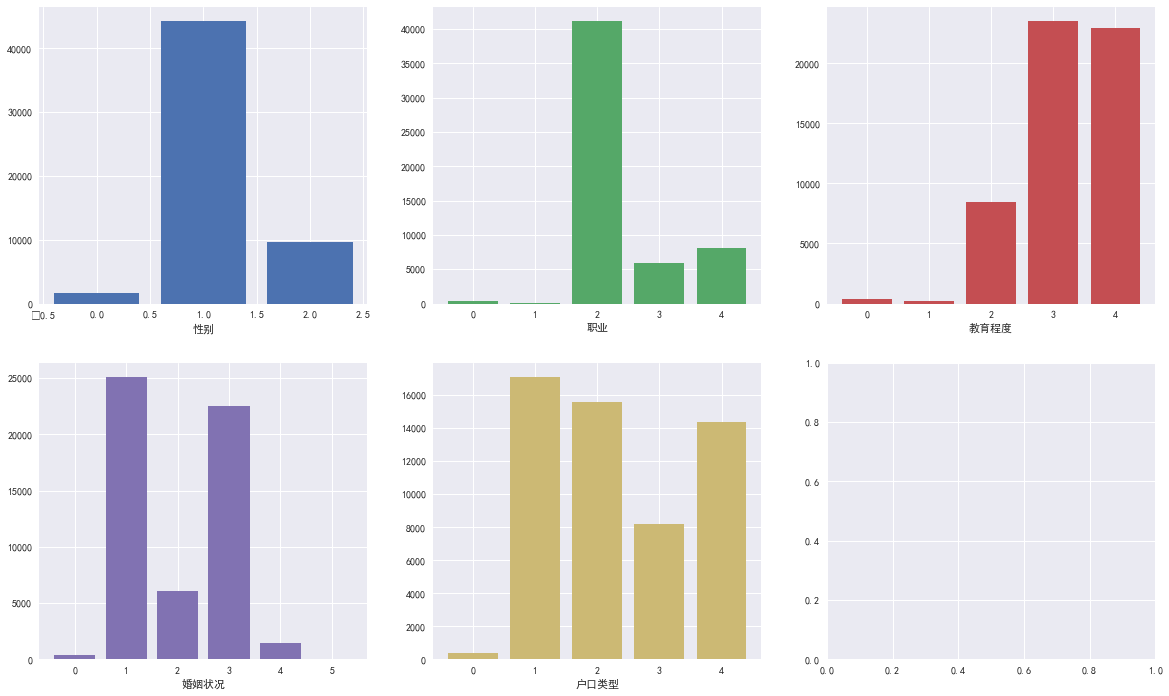
合并属性表和是否逾期表,查看属性与最终是否逾期之间有无明显关系
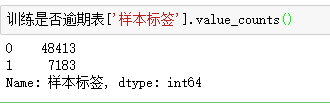
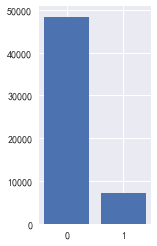
是否逾期表中的数据数量也是55596条,取值分别是0,1 其中0的标签数量明显多于1
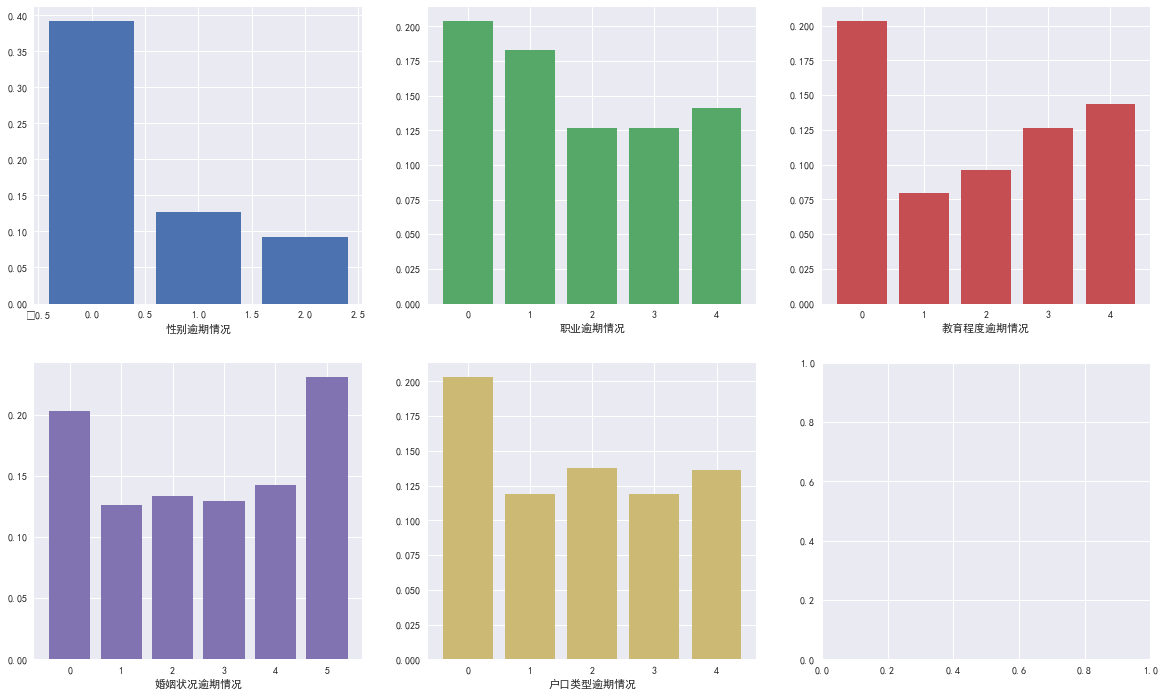
看看用户的属性不同,逾期的比例是不是也不同,这里使用了逾期率

根据前面我们知道:性别中1的数量明显更多,职业中2的职业也更多,受教育程度更多是3,4,婚姻状况更多是1,3,户口类型较为平均
在逾期情况中发现,性别未知的逾期比例最高,2职业最多但是逾期最少,估计是白领。婚姻状况最多是1,3,逾期中最高的是0,5估计是离异等
以上就是全部的属性这个表的分析,接下来看看别的表
二、银行流水记录
银行流水记录表,表中主要是用户支出收入以及工资收入情况,汇总用户的这段时间的总收入总支出合并到前面的统计属性表中去,主要的明细还是支出,数据一共六百多万条
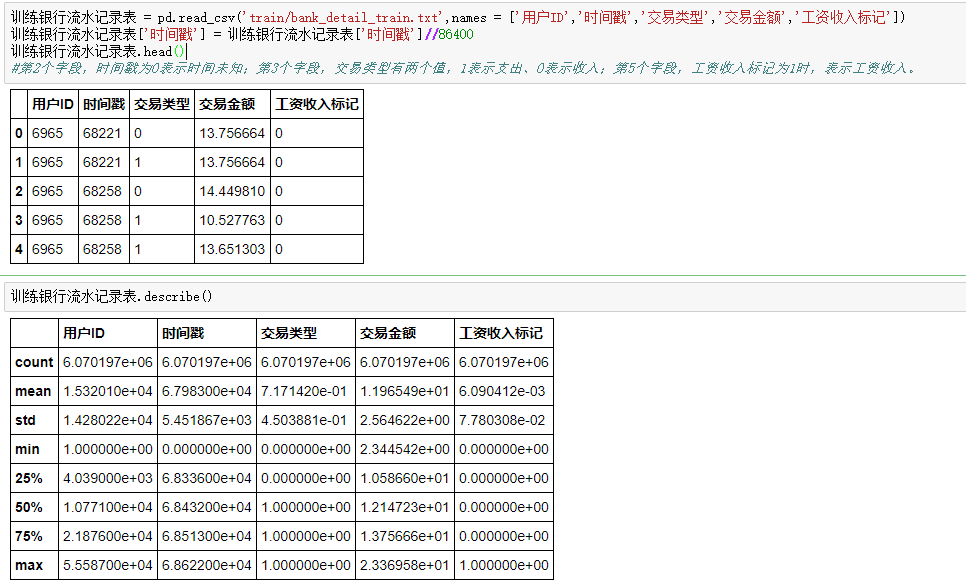
#统计每个用户的支出,收入,工资收入合并到属性表中去 用户支出 = 训练银行流水记录表[训练银行流水记录表['交易类型'] == 1].groupby('用户ID',as_index=False)['交易金额'].agg({'支出次数':np.size,'支出总金额':np.sum}) 用户收入 = 训练银行流水记录表[训练银行流水记录表['交易类型'] == 0].groupby('用户ID',as_index=False)['交易金额'].agg({'收入次数':np.size,'收入总金额':np.sum}) 工资收入 = 训练银行流水记录表[训练银行流水记录表['工资收入标记'] == 1].groupby('用户ID',as_index=False)['交易金额'].agg({'工资收入次数':np.size,'工资总金额':np.sum})
统计属性银行流水表 = pd.merge(统计属性表,用户支出,how='left') 统计属性银行流水表 = pd.merge(统计属性银行流水表,用户收入,how='left') 统计属性银行流水表 = pd.merge(统计属性银行流水表,工资收入,how='left')
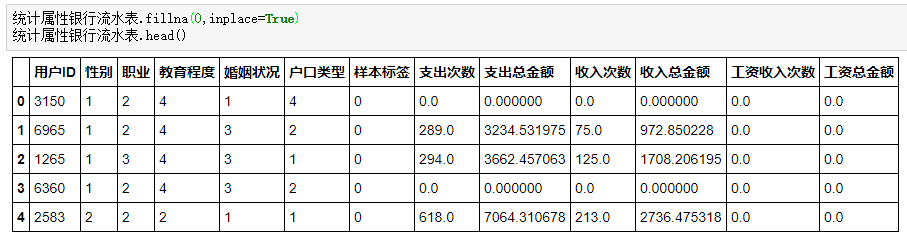
并不是每个用户都有这些数据,所以记得连接时候要用left啊,然后缺失值我们用0填充
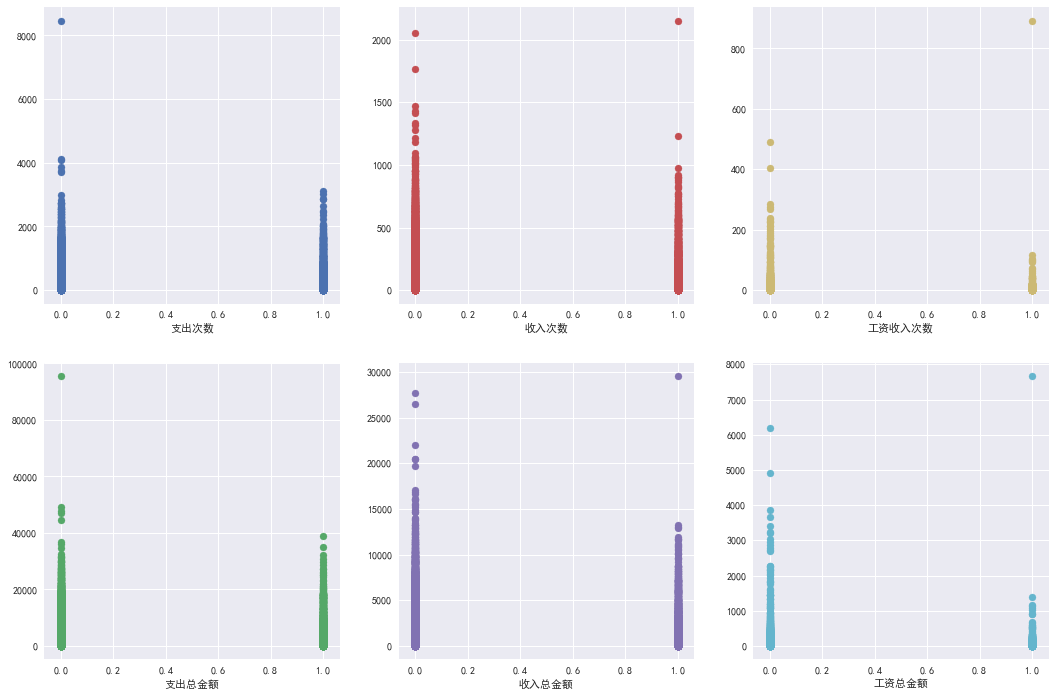
#看看支出,收入,工资收入与是否逾期的关系 fig,ax = plt.subplots(2,3) fig.set_size_inches(18,12) ax[0][0].scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['支出次数'],color = p[0]) ax[0][0].set_xlabel('支出次数') ax[1][0].scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['支出总金额'],color = p[1]) ax[1][0].set_xlabel('支出总金额') ax[0][1].scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['收入次数'],color = p[2]) ax[0][1].set_xlabel('收入次数') ax[1][1].scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['收入总金额'],color = p[3]) ax[1][1].set_xlabel('收入总金额') ax[0][2].scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['工资收入次数'],color = p[4]) ax[0][2].set_xlabel('工资收入次数') ax[1][2].scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['工资总金额'],color = p[5]) ax[1][2].set_xlabel('工资总金额')
在逾期1中发现收入次数和收入总金额明显少于0的,而在支出中相比差别不大。在支出相差不多情况下,收入越少自然逾期概率越大
#还可以增加一个收入-支出的指数 统计属性银行流水表['净收入'] = 统计属性银行流水表['收入总金额'] - 统计属性银行流水表['支出总金额'] fig,ax = plt.subplots() fig.set_size_inches(6,6) ax.scatter(统计属性银行流水表['样本标签'],统计属性银行流水表['净收入'])
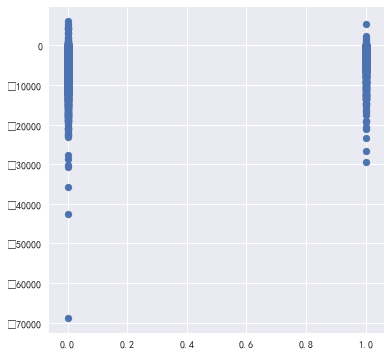
以上就是银行流水记录表,如果想要研究还可以看看各个性别,职业,教育水平的工资、收入、支出等信息对比,这里由于研究的主要是逾期情况,因此主要跟逾期情况做对比
三、信用卡账单记录表
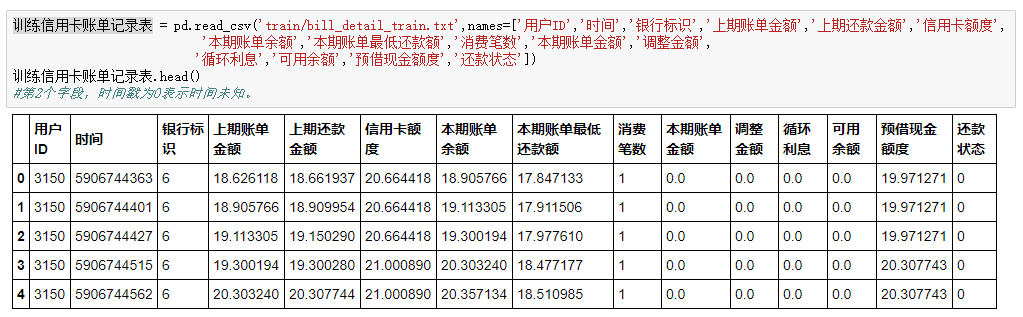
一共两百多万条数据,十五个字段,