转载:https://blog.csdn.net/donggui8650/article/details/101556041
在概率论中,对数正态分布是一种连续概率分布,其随机变量的对数服从正态分布。
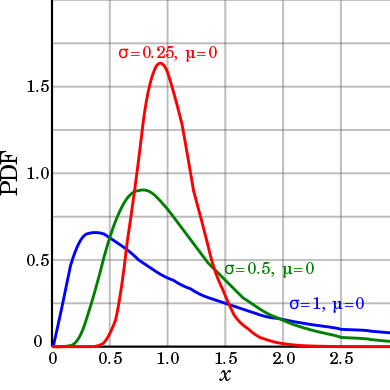
从统计学角度理解对数正态分布是这样的,在自然界有很多事物有增长速度很慢,甚至可以忽略不计(small percentage changes),但是其效果是对整个事物的影响,即每次增长都是对前面增长的乘积运算,但如果我们把他放入对数域,则可以放大他们的增长效果。
假设:x1,x2,...,xk表示第i个单位时间的单位增长率,则x1,x2,...xk大于等于0,令zi=log(xi)表示xi的对数,显然有:
因为x1,x2,...xk独立同分布,显然z1,z2...zk也是独立同分布,则根据中心极限定理(当样本量足够大时,样本均值的分布(变量和的分布)慢慢变成正态分布)有: