数据的标准化(Standardization)和归一化(Normalization)有什么区别?
关于数据的标准化和归一化区别的说法有点乱。总的来说有这么几种分法
1:不做区分,都意味着标准化。
2:大部分说法是这样的:归一化是这么一个过程$x’ = frac{x-x_{min}}{x_{max}-x_{min}}$
而标准化是这么一个过程: $x’ = frac{x-mu}{delta} mu为数据的均值 delta为方差$
3:sklearn当中preprocessing中方法是这样进行划分的:这里的标准化包含了$frac{x-x_{min}}{x_{max}-x_{min}}$和$frac{x-mu}{delta}$ 。归一化则代表把一个样本(而不是特征)的数据进行范数归一化。
我们本篇文章采用第三种分发,而把本文当中所有对数据进行的操作都叫做缩放(scale)。
为什么要进行数据的缩放
消除数据的量纲,这个过程叫做无量纲化。
无量纲化:我们的数据一般都是有单位的,比如身高的单位有m,cm,这个无量纲化并不是说把m变成cm,而是说,无论是m还是cm,最后都会变成1,也就是没有了单位。比如 当前身高的单位为cm,经过这个式子的处理:$x’ = frac{x-x_{最小身高}}{x_{最大身高}-x_{最小身高}}$ 变成了一个没有单位的数字。
当两个特征的量级差别很大的时候,这样的操作是有意义的,假如你有身高和体重两个个特征。身高的单位是m,它的取值经常是这样的值:1.65,1,70,1.67等,而体重的单都位是kg,它经常取这样的值:53,68,73等,我们可以看到体重的值要远远大于身高的值,它们已经不是一个量级了。进行数据的缩放可以避免我们的结果由取值较大的特征决定。
加快模型的收敛速度
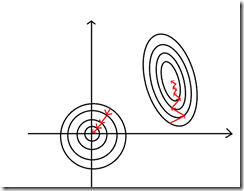
在上图当中,右上角表示在没有进行缩放以前模型的收敛情况,左边表示在进行缩放以后模型收敛的情况。在SVM、线性回归还有PCA当中经常用到。
标准化 Standardization
数据的标准化Standardization,也叫作(去中心化+方差缩放),通过把一组数据的均值变为0,方差变为1实现数据的缩放。数据的标准化是我们对数据的进行缩放的时候最容易想到的操作,也是最常用到的操作。它也叫z-score方法。
自己写一个公式来进行标准化:
def my_scale(data): mean = sum(data) / len(data) #先求均值 variance = ( sum([ (I-mean) ** 2 for I in data]) ) / len(data) #再求方差 normal = [(I - mean) / (variance ) ** 0.5 for I in data] #按照公式标准化 return normal
使用scale方法进行标准化
from sklearn import preprocessing import numpy as np X_train = np.array([[ 1., -1., 2.], [ 2., 0., 0.], [ 0., 1., -1.]]) X_scaled = preprocessing.scale(X_train) print(X_scaled)
输出的结果为:
[[ 0. -1.22474487 1.33630621] [ 1.22474487 0. -0.26726124] [-1.22474487 1.22474487 -1.06904497]]
使用StandardScaler方法进行标准化
StandarScaler方法能够允许我们进行fit,从而保存我们的模型,然后进行transform转换
from sklearn import preprocessing scaler = preprocessing.StandardScaler().fit(X_train) print(scaler.transform(X_train))
输出同样的结果。
将结果缩放到一个区间内
MaxMinScaler方法
MaxMinScaler是将数值缩放到[0,1]区间内,使用的公式是$frac{x-x_{min}}{x_{max}-x_{min}}$
使用这个缩放的情况包括:增强极小方差的值还有保留稀疏样本中的零值。也叫作最大最小标准化,[0,1]标准化。
import numpy as np from sklearn import preprocessing X_train = np.array([[ 1., -1., 2.], [ 2., 0., 0.], [ 0., 1., -1.]]) min_max_sacler = preprocessing.MinMaxScaler() min_max_sacler.fit(X_train) print(min_max_sacler.transform(X_train))
输出的结果为:
[[0.5 0. 1. ] [1. 0.5 0.33333333] [0. 1. 0. ]]
MaxAbsScaler方法
MaxAbsScaler将值缩放到[-1,1]区间内,$frac{x}{max{|x|}}$ 也就是将x除以那个最大的绝对值。这种情况适合在均值在0附近的值,或者稀疏矩阵。
import numpy as np from sklearn import preprocessing X_train = np.array([[ -4., -2., 2.], [ -5., 0., 0.], [ 0., 1., 6.], [10, 2, 3]]) max_abs_sacler = preprocessing.MaxAbsScaler() max_abs_sacler.fit(X_train) print(max_abs_sacler.transform(X_train))
输出结果如下:(第一列除以10,第二列除以4,第三列除以6)
[[-0.4 -1. 0.33333333] [-0.5 0. 0. ] [ 0. 0.25 1. ] [ 1. 0.5 0.5 ]]
特殊数据缩放:
缩放稀疏数据: 使用MaxAbsScaler可以进行稀疏数据的缩放,
缩放异常点较多的数据: 使用robust_scale 或者RobustScaler
非线性转换 -- 分位数转换:
这里主要介绍QuantileTrasformer,和前面提到的缩放一样,分位数转换的目的也是把特征数据转换到一定的范围内,或者让他们符合一定的分布。分位数转换利用的是数据的分位数信息进行变换。它能够平滑那些异常分布,对于存在异常点的数据也很适合。但是它会破话原来数据的相关性和距离信息。
preprocessing的QantitleTransformer可以进行分位数转换
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn import preprocessing import numpy as np iris = load_iris() X, y = iris.data, iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) quantile_transformer = preprocessing.QuantileTransformer(random_state=0) X_train_trans = quantile_transformer.fit_transform(X_train) X_test_trans = quantile_transformer.fit_transform(X_test) #查看分位数信息,经过转换以后,分位数的信息基本不变 print(np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]))
print(np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100]))
输出结果如下:
[4.3 5.1 5.8 6.5 7.9]
[9.99999998e-08 2.38738739e-01 5.09009009e-01 7.43243243e-01
9.99999900e-01]
至于具体的运算规则:猜测可能涉及到分位数回归的知识,这里就没有继续探索。
归一化 Normalization
需要说明是,这里的归一化不是对一列的特征进行操作,而是对一行的样本(记录)进行操作。归一化适用于这样的场景:需要使用点积,或者有的模型需要对样本的相似性进行度量。
preprocessing中的normalize方法提供了这样的操作,这个方法有个参数叫做norm,取值可以为 ‘l1’,’l2’,’max’,取不同的值,使用不同的方式进行归一化。当取值为’l1‘的时候,运用l1范数进行归一化,计算的方法是 $x’ = frac{x}{sum_{i=1}^{n}|x_i|}$ 运用l2范数进行归一化的时候,计算方法是这样的:$x’ = frac{x}{sqrt{sum_{i=1}^{n}x_i^2}}$我们来用代码来看一下:
from sklearn import preprocessing X = [[ 1., -1., 2.], [ 2., 0., 0.], [ 0., 1., -1.], [ 3., 4., 5.]] X1_normalized = preprocessing.normalize(X, norm='l1') X2_normalized = preprocessing.normalize(X, norm='l2') print(X1_normalized) print(X2_normalized)
输出结果如下:
[[ 0.25 -0.25 0.5 ] [ 1. 0. 0. ] [ 0. 0.5 -0.5 ] [ 0.25 0.33333333 0.41666667]] [[ 0.40824829 -0.40824829 0.81649658] [ 1. 0. 0. ] [ 0. 0.70710678 -0.70710678] [ 0.42426407 0.56568542 0.70710678]]
另外preproceing 的Normalizer也提供了标准化的方法,可以进行fit和transform操作。