2016/5/23 星期一 11:00
| desc | |
| 各个公司的核心业务 |
电商主要做推荐
搜索主要做CTR
图像的话,主要应用DL
|
| 无监督 | pca, svd,聚类,GMM |
| 知道高斯混合模型 |
高斯混合就是:
1. 是一种无监督的聚类手段,而且是软聚类,即 给出的每一个 data 数属于各个类的概率
2. 拟合任意分布的概率密度函数
【观点】使用高斯分布拟合 任意分布
|
| 聚类算法的应用 |
一般不作为单独任务,因为结果不确定
聚类可以产生一些 feature ,比如 某个 user_id 对聚类后的结果,可以进行某些关联
聚类的应用:
1. 图片分割,用于 ps 等图像处理当中,把相同颜色的区域选中
2. 邮件归类
3. 用户购买轨迹的 聚类,地址的聚类等等
|
|
计算Fisher 值
一个新的指标
|
(类间的距离÷类内的距离)
表征数据的内聚程度
|
| 聚类中的特征映射 |
聚类不一定都是 凸函数的聚类,比如
需要使用特征映射,即:构造平方项
作为特征,然后你会发现 这种聚类也是可以 聚出来的
就像分类一样
 |
| 聚类一般不使用余弦距离 |
很多聚类库里面是没有 欧式聚类的
余弦距离:在数学上不能被证明保证是会收敛的
因为欧式距离的 中心是可以观测的
|
| 概率密度函数拟合的方法 |
拟合一个概率分布方法
1. 最大熵模型当中的满足某些约束条件的 任意 概率密度的通用表示方法
2. 混合高斯模型,可以拟合任意的
|
|
kmeans 升级
如何初始化敏感情况
|
1. 使用 k-means++ 的方法,随机初始化一个点作为中心点,然后再选next 中心点,要求next 中心点 距离上一个 中心点最远,第三个中心点为 距离前面两个点的距离和最大,即 尽可能选择距离他俩都远的点。
2. 多初始化几遍,然后选其中 损失函数最小的一种
一般有两种形式:
1. 随机初始化中心点,不一定是选点
2. 选取data set 中的一些点 作为 初始中心点
|
|
kmeans 升级
k值如何选定
|
1. 肘点法
对每一个聚类的损失函数作图,然后寻找肘点,作为 最适合的 k
肘点之前的k少,损失值大(因为极限情况一个点一类损失为0);
肘点之后的k大,但是因为聚类个数增多,所以不选取
因为要所以尽可能的选类别少的
2. 逐步剔除法的经验:
先聚一次类,有些 cluster 类中的 data 很少,比如只有 2,3 个,所以需要剔除这m个类,
然后按照 k' = k-m 的方法进行聚类
即:可以先聚2000个,然后再按上面的来减去,然后按照 k-m 的方法 再次聚类
3. 借助其他feature 来聚类
比如商品聚类,不是按照图片的图像像素点直接丢,
而是先看商品的文本描述聚下类,然后可以再切分 先 one-hot
先用文本聚类为 200 个
才知道k取值是这么取得,之前面试的时候都是说穷举,用肘点法
4. 使用K 作为惩罚系数
因为我们的初衷就是尽可能少的聚类个数,即 极限的话一个data 一个类,是没有意义的
但是 k 少成一个类的话,那也是没有意义的,此时 λ 需要经验值,而不是交叉验证出来的
因为 k 取两端的极值 都不好,而 λK 仅仅约束 不能太大
|
|
kmeans 升级
何时终止
|
都说直至收敛,但是这是含糊的说法,具体的指标应该如下:
1. 每个cluster 的点到自己中心点的距离之和,这一个标量不再发生变化
2. k 个中心点 不再发生变化
# 第二种方法,需要比较的是 k*n 的变量,所以不如第一个方法简单
|
|
kmeans 升级
kmeans 对于异常点敏感
|
使用 k-median 的方法
每次的中心都是原始数据中的某一个点
认为这种方法可以 有效解决异常点的问题
|
|
kmeans聚类进阶
summary
|
1. 什么时候【终止】:data 到 中心的距离和 不再发生变换 #这个计算量最小
2. 如何【初始化】 初始中心点(因为初始化敏感):多试几次,选取损失最小的,或者每次找相对于上一个中心点最远的
3. 如何【确定 K】:肘点法
4. 如何解决【异常点】问题? k median
|
| kmeans 中的损失函数 |
这里的Rnk 是一个矩阵,就像EM算法中的 Z 矩阵一样
它是 EM 算法的输出,依据它可以得到 model 的输出
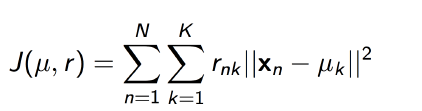 |
| sklearning中的一个参数 |
sklearning 中 kmeans
默认都是聚十次类,选里面 损失函数最小的,它自己都不确定每次初始化是否好
|
| kmeans 和 kmeans++的区别 |
kmeans 是随机初始化的
kmeans++ 每个最远的那个K点初始化
|
| kmeans 和 k-media的区别 |
kmeans 的每次的聚类中心是 计算出来的,可能不属于某个点
kmedian 的聚类,每次的中心都是原始数据中的某一个点
认为这种方法可以 有效解决异常点的问题
|
| 聚类方法的通病 |
1. 初始点敏感 (多试几次,选loss最小;k-means++)
2. 异常点敏感(改进版本的 k-median)
3. 需要手动指定 聚类个数(层次聚类 或者 肘点法 或者 依次剔除法)
4. 对于非凸的数据集 无能为力(可能需要特征映射)
|
| 层次聚类 |
有两种方法:top down 和 bottom up
每一步都只合并两个类
即:一定要做到 最终或者 初始情况是 一个点一个类
基因工程方面用 层次聚类
因为它耗时多,所以其它工程不用这个方法
80W个商品的那个,就不能层次 聚类啊
因为 是 层次聚类一定到 每一个data 一个类
|
| 聚类的一般方法 |
kmeans GMM
其余的就是:
层次聚类,谱聚类
|
| 关于可视化需要降维 | 降维降到两维,才能可视化 |
| 扁平聚类 |
是 相对于 层次聚类而言的
即不是树状的聚类
|
| 一个启发 |
因为尽可能少的聚类个数,因为极限情况一个data 一个类没有意义了
到各自中心点的距离之和 加上 K^2 作为正则化,来选取最优K
因为 K 过大的话,损失是会降低的;但是 K 本身变大会增大损失的值
主要是这个λ系数不好选择,因为 即便选择了适宜的λ,使得损失最小了
那么此时的 聚类结果与k个数 一定是最好的吗?
批评:
因为 k 过多,一个data一个类是没有意义的
k过少,所有data 一个类,也是没有意义的
即 k 应当适中才可以,所以 λ·K 仅仅是约束 k 不能太大,但是 并不是 k 越小越好,所以它没哟约束 k 不能太小,所以这个方法不合适
那么能不能构造一个凸函数:
f(k)—>正无穷,当k—>0
f(k)—>正无穷,当k—>N
或许可以试一下
|
| jieba 分词 |
之前采用的是 最大前向、后向匹配
现在用了 HMM 的方法,即 S M E 作为分词的标注
|
| 聚类的分类 |
1. 软聚类 与 硬聚类
kmeans 属于硬聚类,即一个点只能属于一个类
GMM 可以是软聚类,一个点可以属于多个类(按概率)
2. 扁平聚类 与 树状聚类
扁平聚类,比如 kmeans 聚成某几类是 给定的
树状聚类,比如 层次距离,聚成几类都有
|
| GMM 中的EM 算法 |
M 步骤:
目标函数是
wi = Ni/N # 每个高斯分布的权重
μi = ΣXi/Ni Xi∈第i类 # 均值
Σi = Σ(Xi-μi)·(Xi-μi)^T Xi∈第i类 # 方差
E 步骤:在给定Θ=(w, μ,Σ) 下 data 属于每一个 cluster 的概率
P(cluster = i | xj, Θ),即 Q 函数,即EM 当中的隐变量矩阵 Z
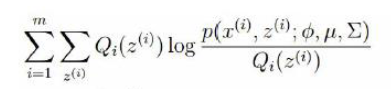 |