1 定义
二叉树是树的一种特殊结构,在二叉树中每个结点最多只能有两个子结点。
二叉树结点的定义如下:
struct BinaryTreeNode { int m_nValue; BinaryTreeNode *m_pLeft; BinaryTreeNode *m_pRight; };
注意:在二叉树的前序遍历序列中,第一个数字总是树的根结点的值。
但在二叉树的中序遍历序列中,根结点的值在序列的中间,其中,左子树的结点的值位于根结点的值的左边,而右子树的结点的值位于根结点的值的右边。因此,我们需要扫描中序遍序序列,才能找到根结点的值。
2 遍历
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根
宽度优先遍历: 先访问树的第一层结点,再访问树的第二层结点…以此类推。
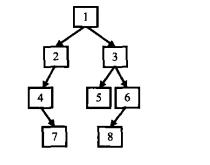
以下图为例:
前序遍历序列{1,2,4,7,3,5,6,8}
中序遍历序列{4,7,2,1,5,3,8,6}
后序遍历序列{7,4,2,5,8,6,3,1}
宽度优先遍历序列{1,2,3,4,5,6,7,8}
3 代码
头文件如下:
#ifndef _BINARY_TREE_ #define _BINARY_TREE_ struct BinaryTreeNode { int m_nValue; BinaryTreeNode *m_pLeft; BinaryTreeNode *m_pRight; }; BinaryTreeNode* CreateBinaryTreeNode(int value); void ConnectTreeNodes(BinaryTreeNode *pParent, BinaryTreeNode *pLeft, BinaryTreeNode *pRight); void PrintTreeNode(BinaryTreeNode *pNode); void PrintTree(BinaryTreeNode *pRoot); void DestroyTree(BinaryTreeNode *pRoot); #endif
cpp文件如下:
#include "BinaryTree.h" #include <stdio.h> BinaryTreeNode *CreateBinaryTreeNode(int value) { BinaryTreeNode *pNode = new BinaryTreeNode(); pNode->m_nValue = value; pNode->m_pLeft = NULL; pNode->m_pRight = NULL; } void ConnectTreeNodes(BinaryTreeNode *pParent, BinaryTreeNode *pLeft, BinaryTreeNode *pRight) { if(pParent) { pParent->m_pLeft = pLeft; pParent->m_pRight = pRight; } } // 一个结点包括3部分,值域以及左右孩子的指针域 // 此处打印,是打印一个完整的结点,包括其自身的值以及左右孩子的值 void PrintTreeNode(BinaryTreeNode *pNode) { if(pNode) { // 自身的值 printf("value of this node is : %d. ", pNode->m_nValue); // 左孩子 if(pNode->m_pLeft) { printf("value of its left child is : %d. ", pNode->m_pLeft->m_nValue); } else { printf("left child is NULL. "); } // 右孩子 if(pNode->m_pRight) { printf("value of its right child is : %d. ", pNode->m_pRight->m_nValue); } else { printf("right child is NULL. "); } } else { printf("this node is NULL. "); } printf(" "); } // 递归 // 前序遍历 // 根左右 void PrintTree(BinaryTreeNode *pRoot) { PrintTreeNode(pRoot); if(pRoot) { if(pRoot->m_pLeft) { PrintTree(pRoot->m_pLeft); } if(pRoot->m_pRight) { PrintTree(pRoot->m_pRight); } } } // 递归销毁 // 根左右 void DestroyTree(BinaryTreeNode *pRoot) { if(pRoot) { BinaryTreeNode *pLeft = pRoot->m_pLeft; BinaryTreeNode *pRight = pRoot->m_pRight; delete pRoot; pRoot = NULL; DestroyTree(pLeft); DestroyTree(pRight); } }