问题提出时,想要利用计算机进行求解,而一般计算机不会分析问题并直接给出解决问题的方案,故我们个人需要分析问题并给出问题的解决方案,再将其描述成计算机能识别的指令(程序),让计算机进行复杂处理,最终得到问题结果,在这一过程中,计算机确起着非常重要的作用,但是要是没有前面的一系列步骤,也不能解决问题
程序设计的一般过程如图所示
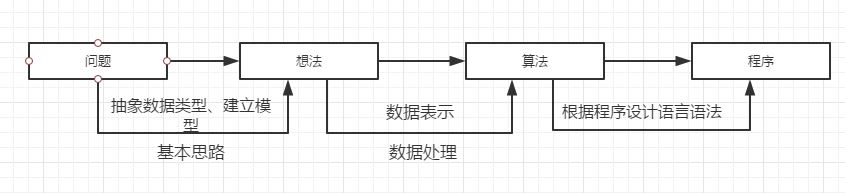
由问题到想法的过程,需要分析待处理的数据以及数据之间的关系,抽象出数据类型,形成基本解题思路。对于数值型问题抽象出来的数据模型一般是数学方程,而非数值类型的问题抽象出来的数据模型一般是表、树、图等数据结构
由想法到算法的过程,需要将人的想法描述成算法(设计算法),即从计算机的角度去思考其是如何一步一步完成任务的,需要考虑数据在计算机上是如何表示(存储)和处理的,将数据模型从机外表示转化为机内表示,描述问题求解的基本思路,将问题的解决想法描述成算法
由算法到程序的过程,需要根据程序设计语言语法,在计算机中对数据进行处理
程序=数据结构+算法(将问题抽象出一个适当的数据结构,然后基于数据结构设计一个好算法)
以七桥问题为例来说明
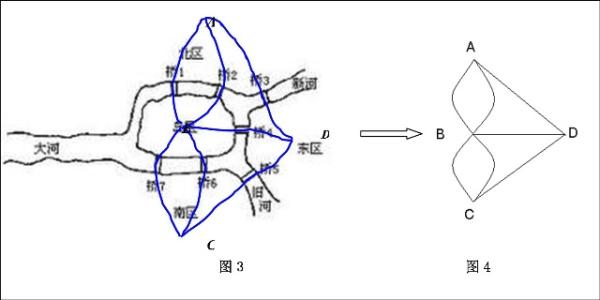
哥尼斯堡,城中有一座岛,有两条支流绕其旁,并将整个城市分为北区、东区、南区和岛区4个区域,全城共有七座桥将四个城区连接起来,如图所示,有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点
| A | B | C | D | |
| A | 0 | 1 | 2 | 2 |
| B | 1 | 0 | 1 | 1 |
| C | 2 | 1 | 0 | 0 |
| D | 2 | 1 | 0 | 0 |
想法:如图所示,将城区抽象为顶点,用A,B,C,D表示4个城区,将桥抽象为边,用7条边表示7座桥,抽象出七桥问题的数据模型如图4所示,从而将七桥问题抽象为一个数学问题:球经过图中每一条边一次且仅一次的回路,后来人们称之为欧拉回路。欧拉回路判定规则是,:
(1)如果没有一个城区通奇数桥,则无论从哪里出发都能找到欧拉回路
(2)如果通奇数桥的城区多于两个,则不存在欧拉回路
(3)如果只有两个城区通奇数桥,则不存在欧拉回路,但可以从这两个城区之一出发准哦到欧拉路径
由上述判定规则得到求解七桥问题的基本思路:依次计算与每个顶点相关联的边数,根据边数为奇数的个数来判定是否存在欧拉回路
算法:将顶点A、B、C、D编号为0,1,2,3,用二维数组array[4][4]存储七桥问题的数据模型,如果将顶点i(0<=i<=3),和顶点j(0<=j<=3)之间有k条边,则元素array[i][j]的值为k,如图所示,求解七桥问题的关键是求与每个顶点的相关联的边数,即是在二维数组array[4][4]中求每一行元素之和,算法如下:
算法:EulerCircuit
输入:二维数组array[4][4]
输出:通奇数桥的顶点个数count
1.count初始化为0;
2.下标i从0~n-1重复执行下述操作:
2.1 计算第i行元素之和degree
2.2 如果degree为奇数,则count++;
3.返回count ;
程序:
#include<stdio.h>
int EulerCircuit(int array[4][4],int n) ;//函数声明,求通奇数桥的顶点个数
int main(){
int array[4][4] ={(0,1,2,2),(1,0,1,1),(2,1,0,0),(2,1,0,0)} ;
int num = EulerCircuit(arrary,4);
if(num>=2){
printf("有%d个地方通奇数桥,不存在欧拉回路 ",num);
else
printf("存在欧拉回路 ");
return 0;
}
int EulerCircuit(int array[4][4],int n){
int i,j,degree,count = 0 ;
for(i = 0 ;i < n ; i++ ){
degree = 0 ;
for(j = 0 ; j < n ; j++){
degree=degree+array[i][j];
}
if(degree%2!=0)
count++;
}
return count ;
}