Codeforces Round #277 (Div. 2) D. Valid Sets (DP DFS 思维)

D. Valid Sets

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:

1. S is non-empty.
2. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S.
3. .

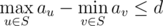Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007(109 + 7).

Input

The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).

The second line contains n space-separated positive integers a1, a2, ..., an(1 ≤ ai ≤ 2000).

Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output

Print the number of valid sets modulo 1000000007.

Examples

input

1 4
2 1 3 2
1 2
1 3
3 4

output

8

input

0 3
1 2 3
1 2
2 3

output

3

input

4 8
7 8 7 5 4 6 4 10
1 6
1 2
5 8
1 3
3 5
6 7
3 4

output

41

Note

In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set {1, 2, 3, 4} is not valid, because the third condition isn't satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.

【题意】给你一棵树，每个节点都有一个 权值a[i],定义一种集合S，不为空，若u，v，属于S，则u->v路径上的所有的点都属于S,且集合中最大权值-最小权值<=d，求 这样的集合个数。

【分析】考虑算每一个节点的贡献。枚举每一个节点，使其成为这个集合的最小值，然后dfs,看他能走多远。dp[u]表示当前节点的子树能形成多少包括u的集合，则dp[u]=dp[u]*(dp[v]+1),v为u的儿子，+1是因为这个儿子形成的集合我可以不取。但是对于权值相同的节点可能形成 一些重复计算的集合，所以要标记一下。

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define met(a,b) memset(a,b,sizeof a)
#define pb push_back
#define mp make_pair
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N = 2e3+5;;
const int M = 160009;
const int mod = 1e9+7;
const int mo=123;
const double pi= acos(-1.0);
typedef pair<int,int>pii;
int n,d;
int a[N],vis[N][N];
ll dp[N],ans;
vector<int>edg[N];
void dfs(int u,int fa,int rt){
    if(a[u]<a[rt]||a[u]-a[rt]>d)return;
    if(a[u]==a[rt]){
        if(vis[rt][u])return;
        else vis[u][rt]=vis[rt][u]=1;
    }
    dp[u]=1;
    for(int v : edg[u]){
        if(v==fa)continue;
        dfs(v,u,rt);
        dp[u]=(dp[u]*(dp[v]+1))%mod;
    }
}
int main(){
    scanf("%d%d",&d,&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1,u,v;i<n;i++){
        scanf("%d%d",&u,&v);
        edg[u].pb(v);edg[v].pb(u);
    }
    for(int i=1;i<=n;i++){
        met(dp,0);
        dfs(i,0,i);
        ans=(ans+dp[i])%mod;
    }
    printf("%lld
",ans);
    return 0;
}