Parliament
Time limit: 1.0 second
Memory limit: 64 MB
Memory limit: 64 MB
A
new parliament is elected in the state of MMMM. Each member of the
parliament gets his unique positive integer identification number during
the parliament registration. The numbers were given in a random order;
gaps in the sequence of numbers were also possible. The chairs in the
parliament were arranged resembling a tree-like structure. When members
of the parliament entered the auditorium they took seats in the
following order. The first of them took the chairman’s seat. Each of the
following delegates headed left if his number was less than the
chairman’s, or right, otherwise. After that he took the empty seat and
declared himself as a wing chairman. If the seat of the wing chairman
has been already taken then the seating algorithm continued in the same
way: the delegate headed left or right depending on the wing chairman’s
identification number.
The
figure below demonstrates an example of the seating of the members of
parliament if they entered the auditorium in the following order: 10, 5,
1, 7, 20, 25, 22, 21, 27.
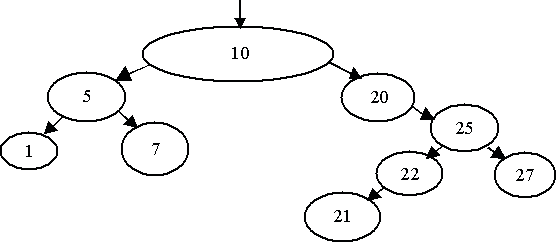
During
its first session the parliament decided not to change the seats in the
future.
The speech order was also adopted. If the number of the session was odd
then the members of parliament spoke in the following order: the left
wing, the right wing and the chairman. If a wing had more than one
parliamentarian then their speech order was the same: the left wing, the
right wing, and the wing chairman. If the number of the session was
even, the speech order was different: the right wing, the left wing, and
the chairman. For a given example the speech order for odd sessions
will be 1, 7, 5, 21, 22, 27, 25, 20, 10; while for even sessions — 27,
21, 22, 25, 20, 7, 1, 5, 10.
Determine the speech order for an even session if the speech order for an odd session is given.
Input
The first line of the input contains N, the total number of parliamentarians. The following lines contain N integer numbers, the identification numbers of the members of parliament according to the speech order for an odd session.
The total number of the members of parliament does not exceed 3000. Identification numbers do not exceed 65535.
Output
The
output should contain the identification numbers of the members of
parliament in accordance with the speech order for an even session.
Sample
| input | output |
|---|---|
9 1 7 5 21 22 27 25 20 10 |
27 21 22 25 20 7 1 5 10 |
Problem Source: Quarterfinal, Central region of Russia, Rybinsk, October 17-18 2001