SPSS聚类与判别

实验目的

　　学会使用SPSS简单操作，掌握聚类与判别。

实验要求

　　使用SPSS。

实验内容

实验步骤

　　（1）层次聚类法分析实例——为了反映中国各地区生活水平差异性，本报告对2002年中国部分省市的国民经济数据进行聚类分析，依次了解我国各省市的生活差异水平，详见“lx17.sav文件”。SPSS操作，点击【分析】→【分类】→【系统聚类】，在打开的【系统聚类分析】对话框中，把GDP、Pindex_Revise等5个变量选入【变量】中，把省份选入【个案标注依据】，点击【图】，勾选【谱系图】，“冰柱图块”勾选【无】→【继续】。点击【方法】，下拉列表，选择【瓦尔德法】，“转换值块”勾选【Z得分】→【继续】。点击【保存】→【解的范围】，3~8→【继续】。单击【确定】。

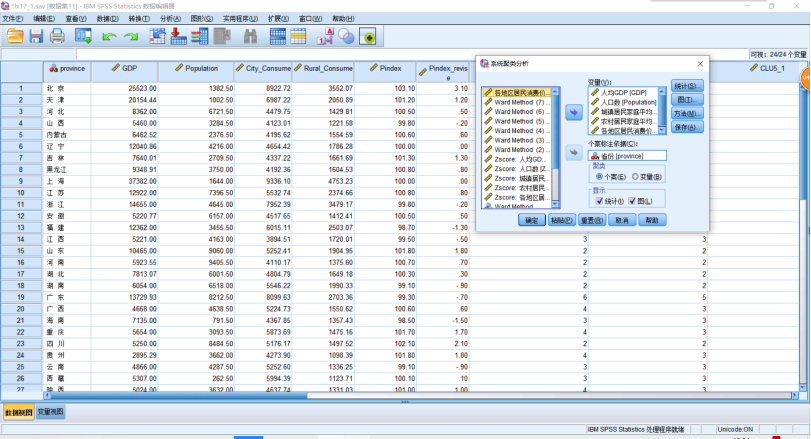
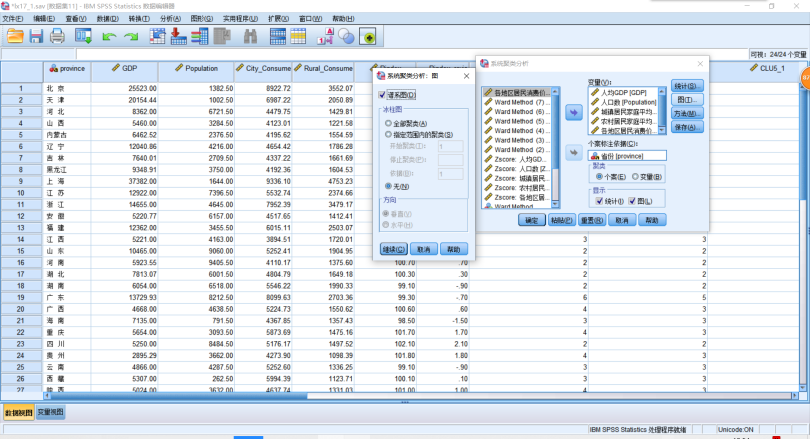
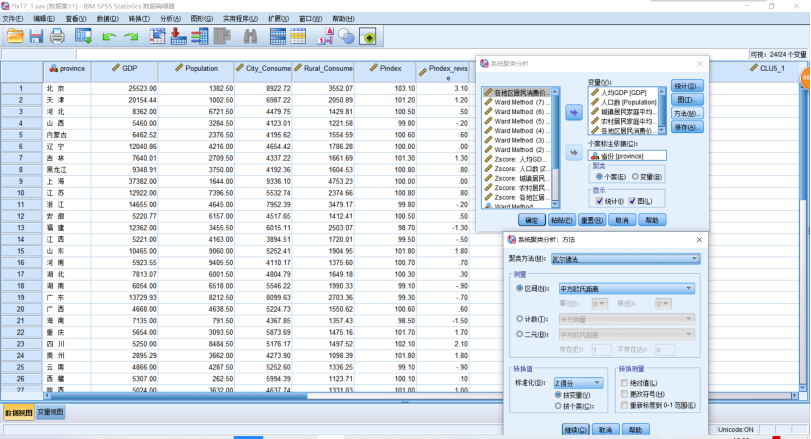
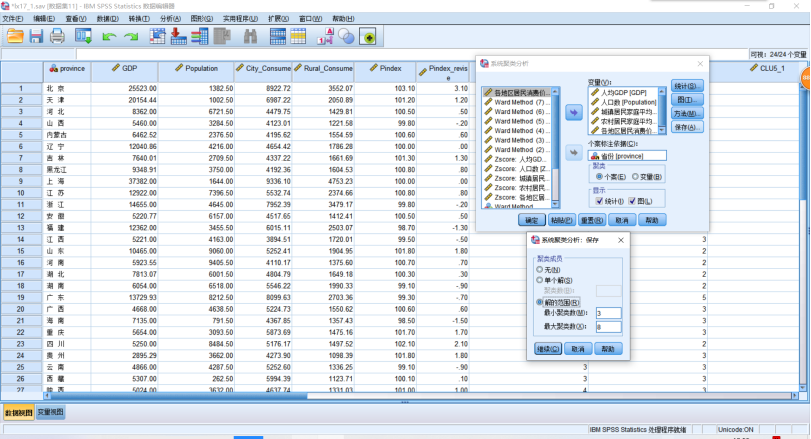
　　运行分析，

集中计划
阶段	组合聚类		系数	首次出现聚类的阶段		下一个阶段
阶段	聚类 1	聚类 2	系数	聚类 1	聚类 2	下一个阶段
1	3	17	.111	0	0	2
2	3	12	.246	1	0	15
3	5	7	.407	0	0	4
4	5	8	.624	3	0	13
5	20	27	.857	0	0	11
6	29	30	1.121	0	0	20
7	28	31	1.390	0	0	20
8	4	14	1.666	0	0	10
9	15	23	2.102	0	0	14
10	4	25	2.751	8	0	21
11	20	24	3.419	5	0	12
12	20	22	4.167	11	0	19
13	5	6	5.010	4	0	19
14	15	16	6.127	9	0	23
15	3	18	7.428	2	0	18
16	21	26	8.813	0	0	21
17	11	19	10.248	0	0	22
18	3	10	12.010	15	0	23
19	5	20	13.835	13	12	25
20	28	29	16.130	7	6	27
21	4	21	18.530	10	16	25
22	11	13	21.298	17	0	28
23	3	15	24.620	18	14	29
24	1	2	28.412	0	0	26
25	4	5	32.928	21	19	27
26	1	9	41.666	24	0	28
27	4	28	54.441	25	20	29
28	1	11	68.972	26	22	30
29	3	4	87.757	23	27	30
30	1	3	150.000	28	29	0

　　需要判别数据应该分成多少类别时，聚类系数那一列有着很好的参考价值。

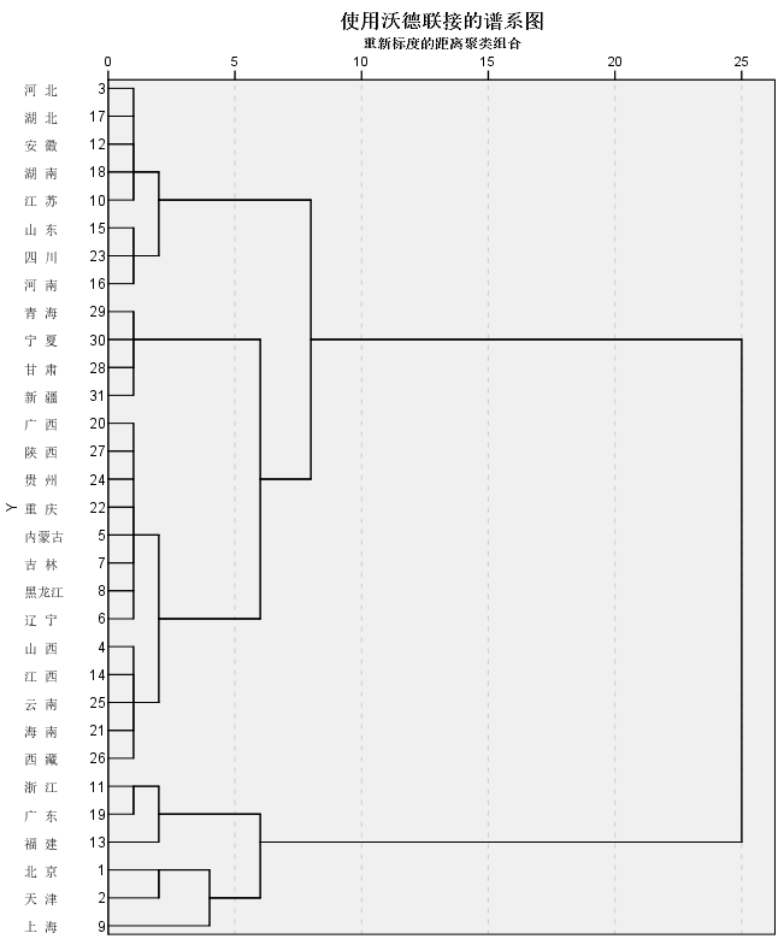
　　（1）方案一：分成6类或者5类。

　　第1类：上海；第二类：北京、天津；第3类：河北、湖北、安徽、湖南、江苏、山东、四川、河南；第4类：广西、峡西、贵州、重庆、内蒙古、吉林、黑龙江、辽宁、山西、江西、云南、海南、西藏；第5类：浙江、广东、福建；第6类：青海、宁夏、甘肃、新疆。

　　事实上，由于在分成6类时，第1个类别只有上海一个城市，所以在这种聚类方法中更倾向于将31个省市分成5类，即将第1类和第2类合并为1类。

　　（2）方案二：分成3类或2类。

　　第1类：上海、北京、天津、浙江、广东、福建；第2类：河北、湖北、安徽、湖南、江苏、山东、四川、河南；第3类：青海、宁夏、甘肃、新疆、广西、峡西、贵州、重庆、内蒙古、吉林、黑龙江、辽宁、山西、江西、云南、海南、西藏。

　　其中第2类和第3类可以并为1类，这时总类别数2。但是由于分成两类区分性不强。常更倾向于分成3类。

　　代码：

 1 DATASET DECLARE D0.6606863886229252.
 2 PROXIMITIES   GDP Population City_Consume Rural_Consume Pindex_revise
 3   /MATRIX OUT(D0.6606863886229252)
 4   /VIEW=CASE
 5   /MEASURE=SEUCLID
 6   /PRINT NONE
 7   /ID=province
 8   /STANDARDIZE=VARIABLE Z.
 9 
10 CLUSTER
11   /MATRIX IN(D0.6606863886229252)
12   /METHOD WARD
13   /ID=province
14   /PRINT SCHEDULE
15   /PLOT DENDROGRAM
16   /SAVE CLUSTER(3,8).

　　进一步分析，【分析】→【比较平均值】→【平均值】。在【平均值】对话框中，把GDP等5个变量选入【因变量列表】，把Ward Method[CLU5_3]选入【层】中。

报告
平均值
Ward Method	人均GDP	人口数	城镇居民家庭平均每人全年消费性支出	农村居民家庭平均每人生活消费支出	各地区居民消费价格指数-100
1	27686.4786	1343.0000	8415.3467	3452.0620	1.4333
2	7751.2991	7468.0625	4927.4875	1704.3075	.7250
3	6286.3535	3143.6154	4694.0031	1447.7899	.3692
4	13582.3095	5437.6667	7355.7100	2895.1985	-.7333
5	5787.7307	1388.0000	4661.4250	1299.2102	3.0500
总计	9377.1057	4080.8226	5367.7681	1828.8500	.8032

　　代码：

1 MEANS TABLES=GDP Population City_Consume Rural_Consume Pindex_revise BY CLU5_3
2   /CELLS=MEAN.

　　【分析】→【比较平均值】→【单因素ANOVA检验】，在打开的对话框中，把GDP等5个变量选入【因变量列表】，把Ward Method[CLU5_3]选入【层】中。

ANOVA
		平方和	自由度	均方	F	显著性
人均GDP	组间	1255616794.261	4	313904198.565	28.659	.000
	组内	284777747.752	26	10952990.298
	总计	1540394542.013	30
人口数	组间	160221068.312	4	40055267.078	21.060	.000
	组内	49451014.962	26	1901962.114
	总计	209672083.274	30
城镇居民家庭平均每人全年消费性支出	组间	49166873.689	4	12291718.422	23.651	.000
	组内	13512763.997	26	519721.692
	总计	62679637.686	30
农村居民家庭平均每人生活消费支出	组间	14449596.776	4	3612399.194	16.422	.000
	组内	5719138.558	26	219966.868
	总计	20168735.335	30
各地区居民消费价格指数-100	组间	30.964	4	7.741	7.360	.000
	组内	27.346	26	1.052
	总计	58.310	30

　　代码：

1 ONEWAY GDP Population City_Consume Rural_Consume Pindex_revise BY CLU5_3
2   /MISSING ANALYSIS.

　　从上述两个表看出，各个类别之间的5个变量都是有显著性差异的，且这些差异均具有统计意义。

　　所以最终的特征类别描述：

　　第1类：高生活水平城市，北京、上海、天津。

　　第2类：人口众多，生活水平一般。北、湖北、安徽、湖南、江苏、山东、四川、河南；

　　第3类：生活水平一般，人口较少。广西、峡西、贵州、重庆、内蒙古、吉林、黑龙江、辽宁、山西、江西、云南、海南、西藏；

　　第4类：消费水平相对人均GDP较高，平均物价水平较低，消费价格指数都小于100。浙江、广东、福建；

　　第5类：人口稀少，生活水平低，平均物价水平高。青海、宁夏、甘肃、新疆。

　　K-均值聚类法（又叫快速聚类）分析示例——移动电话客户使用手机情况，数据详见mobile.sav文件。SPSS操作，先对数据进行描述性统计，【分析】→【描述统计】→【描述】，

L-在【描述】对话框中，把前6个变量选入【变量】中。点击【选项】，勾选【平均值】、【标准差】、【最大值】、【最小值】→【继续】，单击【确定】。（标准化数据：【分析】→【描述统计】→【描述】，在【描述】对话框中，把前6个变量选入【变量】中。勾选【将标准化值另存为变量】）。【分析】→【分类】→【K-均值聚类分析】，在打开的对话框中，把标准化的6个变量选入【变量】中，把客户编号选入【个案标注依据】，【聚类数】填5；点击【迭代】，【最大迭代次数】填写100→【继续】。点击【保存】，勾选【聚类成员】→【继续】。点击【选项】→【统计】，勾选【ANOVA表】→【继续】。单击【确定】。

描述统计
	N	最小值	最大值	均值	标准偏差
工作日上班时期电话时长	3395	5.77	2846.40	708.3469	515.25799
工作日下班时期电话时长	3395	3.20	1058.40	301.8049	195.33152
周末电话时长	3395	.66	205.00	54.1649	35.26109
国际电话时长	3395	.01	1014.82	172.3492	146.68342
总通话时长	3395	54.81	3423.30	1064.3168	560.80133
平均每次通话时长	3395	.63	53.58	4.1267	3.80400
有效个案数（成列）	3395

　　代码：

1 DESCRIPTIVES VARIABLES=Peak_mins OffPeak_mins Weekend_mins International_mins Total_mins
2     average_mins
3   /STATISTICS=MEAN STDDEV MIN MAX.

　　从表中可见，尽管数据的量纲是一样的，但是数据的取值却仍然有很大差别，平均数据从最小的4.1267到最大的1046.3168等。为了消除这种差异，需要事先对数据标准化。

　　代码：

1 DESCRIPTIVES VARIABLES=Peak_mins OffPeak_mins Weekend_mins International_mins Total_mins
2     average_mins
3   /SAVE
4   /STATISTICS=MEAN STDDEV MIN MAX.

初始聚类中心
	聚类
	1	2	3	4	5
Zscore: 工作日上班时期电话时长	3.21791	-1.16165	2.64849	.19729	1.93001
Zscore: 工作日下班时期电话时长	-.65276	-1.26557	-1.03058	3.87339	-.17204
Zscore: 周末电话时长	3.72181	3.11491	-.02169	-.90652	-1.21281
Zscore: 国际电话时长	4.90995	-1.16636	.29390	2.77257	.53252
Zscore: 总通话时长	2.96323	-1.31226	2.07308	1.47340	1.63709
Zscore: 平均每次通话时长	-.51651	.30760	5.49282	-.22792	12.99993

　　它列出每一类别初始定义的中心点，实际上就是数据集中的某一条记录，其选择的原则是使得各初始类中心的散点在所有变量构成的空间中离的尽可能远，而且能尽量广地分布在空间中。

迭代历史记录^a
迭代	聚类中心中的变动
迭代	1	2	3	4	5
1	3.894	3.450	3.201	3.605	3.458
2	.829	.207	.725	.312	1.943
3	.374	.127	.457	.262	.964
4	.208	.100	.330	.206	.504
5	.156	.060	.219	.141	.421
6	.116	.047	.168	.116	.337
7	.104	.041	.164	.105	.134
8	.110	.035	.140	.111	.188
9	.077	.028	.105	.101	.081
10	.069	.022	.117	.082	.057
11	.054	.020	.148	.079	.000
12	.028	.030	.198	.054	.063
13	.063	.055	.309	.044	.119
14	.105	.077	.363	.058	.263
15	.126	.074	.276	.068	.193
16	.118	.029	.140	.048	.152
17	.072	.016	.108	.049	.172
18	.046	.008	.080	.053	.087
19	.037	.011	.076	.050	.083
20	.034	.010	.055	.036	.113
21	.020	.009	.051	.036	.113
22	.017	.008	.028	.016	.115
23	.026	.006	.026	.014	.000
24	.010	.004	.032	.023	.000
25	.010	.004	.020	.015	.000
26	.009	.004	.013	.009	.053
27	.006	.002	.006	.007	.000
28	.000	.004	.004	.009	.000
29	.000	.003	.006	.006	.000
30	.000	.000	.010	.010	.000
31	.005	.002	.011	.009	.000
32	.008	.001	.007	.005	.000
33	.004	.000	.002	.001	.000
34	.007	.000	.004	.000	.000
35	.000	.000	.000	.000	.000
a. 由于聚类中心中不存在变动或者仅有小幅变动，因此实现了收敛。任何中心的最大绝对坐标变动为 .000。当前迭代为 35。初始中心之间的最小距离为 7.609。

　　从上表可以看出，每一次迭代过程中类别中心的变化。类别中心点变化越来越小，知道趋近与0。整个迭代过程在第35步终止，因为此时已经满足了上面提到的迭代终止的第2个标准，所以可以认为各类别中心已经收敛了。

最终聚类中心
	聚类
	1	2	3	4	5
Zscore: 工作日上班时期电话时长	1.60559	-.78990	.61342	-.33584	.37303
Zscore: 工作日下班时期电话时长	.46081	-.58917	-.49365	1.18873	-.29014
Zscore: 周末电话时长	-.14005	-.15010	.35845	-.02375	-.40407
Zscore: 国际电话时长	1.68250	-.64550	.04673	.02351	-.04415
Zscore: 总通话时长	1.62690	-.94040	.41420	.10398	.21627
Zscore: 平均每次通话时长	-.06590	-.14835	-.05337	-.14059	4.87718

　　Means生成的另一个比较重要的结果是最终的类别中心点，也就是各个类别在各个变量上的平均值。

ANOVA
	聚类		误差		F	显著性
	均方	自由度	均方	自由度	F	显著性
Zscore: 工作日上班时期电话时长	582.315	4	.314	3390	1854.022	.000
Zscore: 工作日下班时期电话时长	468.001	4	.449	3390	1042.395	.000
Zscore: 周末电话时长	39.060	4	.955	3390	40.896	.000
Zscore: 国际电话时长	443.179	4	.478	3390	926.658	.000
Zscore: 总通话时长	605.770	4	.286	3390	2115.071	.000
Zscore: 平均每次通话时长	463.823	4	.454	3390	1021.872	.000
由于已选择聚类以使不同聚类中个案之间的差异最大化，因此 F 检验只应该用于描述目的。实测显著性水平并未因此进行修正，所以无法解释为针对“聚类平均值相等”这一假设的检验。

　　得出结论，各个变量对聚类结果的重要程度排序为：总通话时长>工作日上班电话时长>工作日下班时期电话时长>平均每次通话时长>国际电话时长>周末电话时长。

每个聚类中的个案数目
聚类	1	443.000
	2	1239.000
	3	831.000
	4	806.000
	5	76.000
有效		3395.000
缺失		.000

　　可见人数最多的是第2类，而最少的是第5类，第1类人群也较少，各类人数的高低有时可以为最终类别特性的确定起都辅助作用。

　　最终类别特征描述：

　　第1类：高端商用客户，总通话时间长，工作日上班通话比例高用户，443人。

　　第2类：少使用低端客户，总通话时间短，各个时段通话时间都短，1239人。

　　第3类：中端商用客户，总通话时间居中，工作日上班通话比例高用户，831人。

　　第4类：中端日常用客户，总通话时间居中，工作日下班通话比例高用户，806人。

　　第5类：长聊客户，每次通话时间长客户，76人。

1 QUICK CLUSTER ZPeak_mins ZOffPeak_mins ZWeekend_mins ZInternational_mins ZTotal_mins Zaverage_mins
2   /MISSING=LISTWISE
3   /CRITERIA=CLUSTER(5) MXITER(100) CONVERGE(0)
4   /METHOD=KMEANS(NOUPDATE)
5   /SAVE CLUSTER
6   /PRINT ID(Customer_ID) INITIAL ANOVA.

　　两步聚类法实例分析——例子是患有某种疾病的患者的病例数据，详细见drug.sav数据文件。SPSS操作，【分析】→【分类】→【二阶聚类】，把Sex,BP,Cholesterol选入【分类变量】中，把Age,Na,K选入【连续变量】中。点击【输出】，勾选【透视表】和【创建聚类成员变量】→【继续】。单击【确定】。

运行示例，

自动聚类
聚类数目	施瓦兹贝叶斯准则 (BIC)	BIC 变化量^a	BIC 变化比率^b	距离测量比率^c
1	3579.426
2	2941.099	-638.327	1.000	1.835
3	2621.569	-319.530	.501	1.202
4	2366.305	-255.264	.400	1.715
5	2243.387	-122.918	.193	1.016
6	2123.381	-120.006	.188	1.046
7	2011.454	-111.926	.175	1.265
8	1935.996	-75.458	.118	1.139
9	1877.369	-58.627	.092	1.062
10	1825.830	-51.539	.081	1.100
11	1784.648	-41.181	.065	1.293
12	1766.882	-17.767	.028	2.591
13	1798.181	31.299	-.049	1.099
14	1832.250	34.070	-.053	1.037
15	1867.309	35.059	-.055	1.035
a. 变化量基于表中的先前聚类数目。
b. 变化比率相对于双聚类解的变化。
c. 距离测量比率基于当前聚类数目而不是先前聚类数目。

　　（1）确认最佳聚类类别数时最重要的指标是BIC值，即Bayes信息准则，其数值越小代表效果越好，而其右侧的BIC Change列则反映相邻两种结果的BIC之差，可见BIC值以12类时最小，但在8类后，BIC下降不太明显。综合观察，可以认为4~8类都是可供考虑的选择范围。

　　（2）除BIC值外，两步聚类法还会利用相邻的两步的最小间距离比来进一步确认最佳的类别数。最小间距离比共有3个高峰，分别对应了2类、4类和12类的情形。以12类时为例，其数值为2.655，意思是和聚为13类时的最小类间距相比，12类时的最小间距离是它的2.655倍。由于第2步是采用的是层次聚类法，这些结果是嵌套的关系，因此，这就意味着在原来12类的基础上再拆分出的两个新类相比之下其实差别很小，空拍意义不大。显然，该指标越大，表示当前结果越好。结合前面的BIC大小，可以认定对于本利而言，4类或者12类时统计上认为最佳的类别数。

聚类分布
		个案数	占组合的百分比	占总计的百分比
聚类	1	134	26.8%	26.8%
	2	136	27.2%	27.2%
	3	98	19.6%	19.6%
	4	132	26.4%	26.4%
	组合	500	100.0%	100.0%
总计		500		100.0%

　　确定聚为4类后，可以看出每个类别包含记录数目大体相差不大。

质心
		年龄		钠含量		钾含量
		平均值	标准偏差	平均值	标准偏差	平均值	标准偏差
聚类	1	42.72	17.102	.7319	.11601	.0483	.01801
	2	45.57	17.505	.6919	.11797	.0507	.01639
	3	44.54	18.345	.7244	.11215	.0500	.01756
	4	44.08	16.186	.6872	.11396	.0501	.01740
	组合	44.21	17.210	.7078	.11661	.0498	.01730

　　可见对于钠含量而言，第3类的均数最高，而第4类中钠含量的均数最低。

　　代码

 1 TWOSTEP CLUSTER
 2   /CATEGORICAL VARIABLES=血压 胆固醇 性别
 3   /CONTINUOUS VARIABLES=年龄 钠含量 钾含量
 4   /DISTANCE LIKELIHOOD
 5   /NUMCLUSTERS AUTO 15 BIC
 6   /HANDLENOISE 0
 7   /MEMALLOCATE 64
 8   /CRITERIA INITHRESHOLD(0) MXBRANCH(8) MXLEVEL(3)
 9   /VIEWMODEL DISPLAY=YES
10   /PRINT IC COUNT SUMMARY
11   /SAVE VARIABLE=TSC_5167.

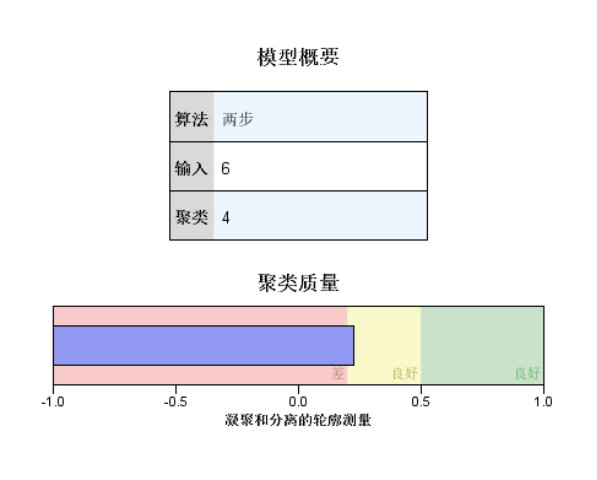
　　数据作图，【图性】→【旧对话框】→【误差条形图】→【简单】→【个案组摘要】，在打开的对话框中，把“钠含量”选入【变量】，把“二阶聚类编号”选入【类别轴】→【确定】。

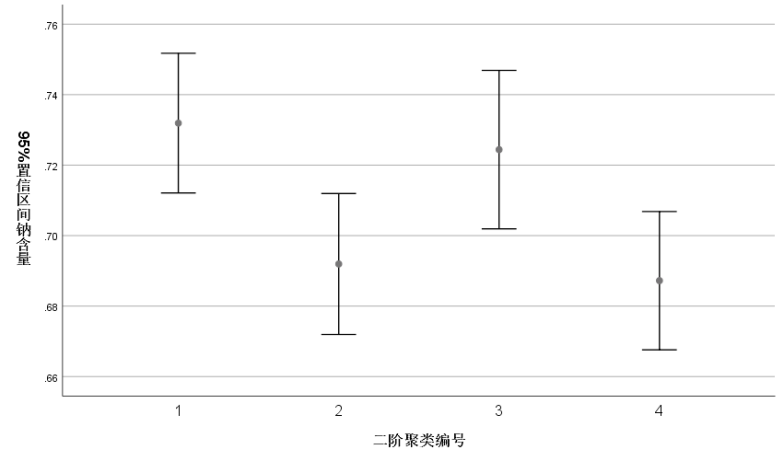
1 GRAPH
2   /ERRORBAR(CI 95)=钠含量 BY TSC_5167

　　做图分析，SPSS操作，【图形】→【旧对话框】→【直方图】，把“二阶聚类编号”选入【变量】，把“性别”选入【列】→【确定】。

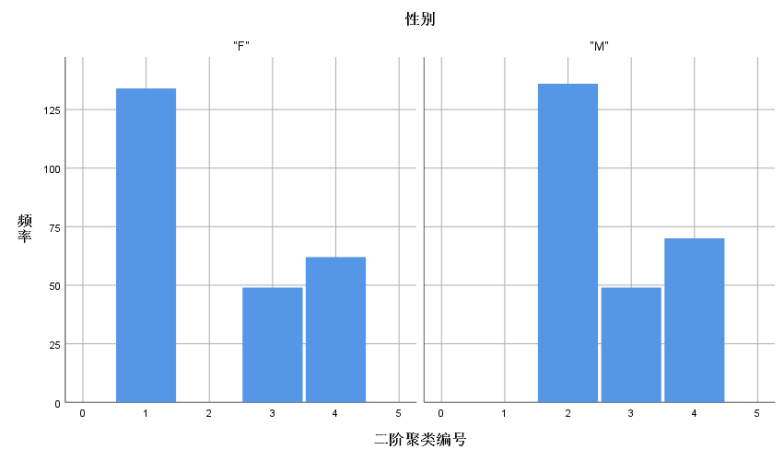
1 GRAPH
2   /HISTOGRAM=TSC_5167
3   /PANEL COLVAR=性别 COLOP=CROSS.

　　由上所画的统计图可见钠含量的变化情况和表格基本一致，而离散变量性别而言，第3类和第4类男性和女性基本是等比例的，而第1类中只有男性，第2类中只有女性。

　　最终类别描述：

　　第1类：女性、胆固醇浓度高。134人，占比26.8%，血液钠含量高于平均水平。

　　第2类：男性、胆固醇浓度高。136人，占比27.2%，血液钠含量低于平均水平。

　　第3类：高血压、胆固醇浓度正常。此类病人数量为98人，占病人总数19.6%，全部为高血压、胆固醇浓度正常，血压无明显特征，血液钠含量高于平均水平。

　　第4类：非高血压、胆固醇浓度正常。132人，占比26.4%，血液钠含量低于平均水平。

　　（3）Fisher判别分析示例——鸢尾花资料，数据详见iris.sav文件。SPSS操作，【分析】

→【分类】→【判别式】，在打开的对话框中，把spno选入【分组变量】，并【定义范围】→【最大值】3→【最小值】1。把除编号外剩下的变量选入【自变量】中→【确定】。

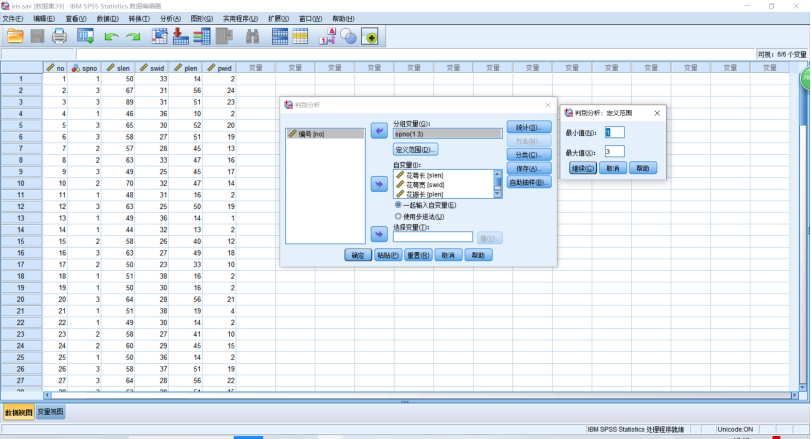
运行示例，

特征值
函数	特征值	方差百分比	累积百分比	典型相关性
1	30.419^a	99.0	99.0	.984
2	.293^a	1.0	100.0	.476
a. 在分析中使用了前 2 个典则判别函数。

　　提取了两个判别函数且绝大部分信息在第1个判别函数上。

威尔克 Lambda
函数检验	威尔克 Lambda	卡方	自由度	显著性
1 直至 2	.025	538.950	8	.000
2	.774	37.351	3	.000

　　两个判别函数各个变量的标准化系数，可用来判断两个函数分别主要受哪些变量的影响较大。

标准化典则判别函数系数
	函数
	1	2
花萼长	-.346	.039
花萼宽	-.525	.742
花瓣长	.846	-.386
花瓣宽	.613	.555

标准化典则判别函数系数
	函数
	1	2
花萼长	-.346	.039
花萼宽	-.525	.742
花瓣长	.846	-.386
花瓣宽	.613	.555

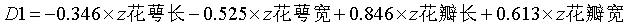
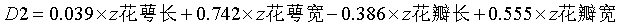
　　变量名前加z表明是标准化后的数值。

结构矩阵
	函数
	1	2
花瓣长	.726^*	.165
花萼宽	-.121	.879^*
花瓣宽	.651	.718^*
花萼长	.221	.340^*
判别变量与标准化典则判别函数之间的汇聚组内相关性变量按函数内相关性的绝对大小排序。
*. 每个变量与任何判别函数之间的最大绝对相关性

　　给出各组的判别函数的重心。在得知各类的重心后，只需要为每个待判个案求出判别得分，然后计算出该个案的散点离哪一个中心最近，就可以得到该个案的判别结果了。

组质心处的函数
分类	函数
分类	1	2
刚毛鸢尾花	-7.392	.219
变色鸢尾花	1.763	-.737
佛吉尼亚鸢尾花	5.629	.518
按组平均值进行求值的未标准化典则判别函数

　　代码：

1 DATASET ACTIVATE 数据集39.
2 DATASET CLOSE 数据集38.
3 DISCRIMINANT
4   /GROUPS=spno(1 3)
5   /VARIABLES=slen swid plen pwid
6   /ANALYSIS ALL
7   /PRIORS EQUAL
8   /CLASSIFY=NONMISSING POOLED.

　　如果希望得到直接使用原始变量的判别函数，则可以在【判别分析】的对话框中，点击【统计】，勾选【未标准化】，点击【继续】，【确定】。

　　运行示例，

典则判别函数系数
	函数
	1	2
花萼长	-.063	.007
花萼宽	-.155	.218
花瓣长	.196	-.089
花瓣宽	.299	.271
(常量)	-2.526	-6.987
未标准化系数

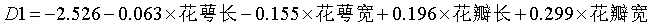
1 DISCRIMINANT
2   /GROUPS=spno(1 3)
3   /VARIABLES=slen swid plen pwid
4   /ANALYSIS ALL
5   /PRIORS EQUAL
6   /STATISTICS=RAW
7   /CLASSIFY=NONMISSING POOLED.

　　判别结果图形化展示，在【判别分析】的对话框中，点击【分类】，勾选【合并图】和【邻域图】，点击【继续】，【确定】。

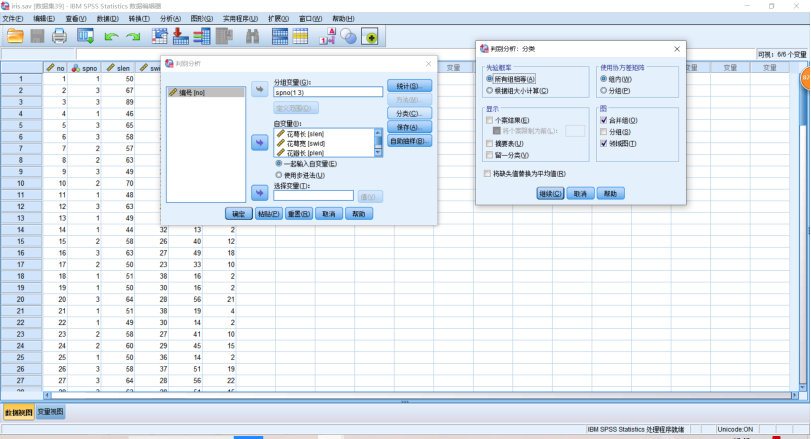
　　运行示例，

领域图

典则判别

函数 2

-16.0 -12.0 -8.0 -4.0 .0 4.0 8.0 12.0 16.0

+---------+---------+---------+---------+---------+---------+---------+---------+

16.0 + 13 +

I 13 I

I 123 I

I 12 23 I

12.0 + + + + 12 23 + + + +

I 12 23 I

8.0 + + + + 12 + 23 + + + +

I 12 23 I

4.0 + + + + 12 + 23 + + + +

I 12 23 I

I 12 23 * I

.0 + + + * + 12 + 23 + + +

I 12 * 23 I

I 12 23 I

-4.0 + + + + 12 + + 23 + + +

I 12 23 I

-8.0 + + + +12 + + 23 + + +

I 12 23 I

-12.0 + + + 12 + + 23 + +

I 12 23 I

-16.0 + 12 23 +

+---------+---------+---------+---------+---------+---------+---------+---------+

-16.0 -12.0 -8.0 -4.0 .0 4.0 8.0 12.0 16.0

典则判别函数 1

领域图中使用的符号

符号分组标签

------ ------ ----------------------

1 1 刚毛鸢尾花

2 2 变色鸢尾花

3 3 佛吉尼亚鸢尾

* 指示组质心

　　当新案例被计算出来散点坐标后，即可被绘制在该图形中，该坐标点落在那个范围，就应当属于哪个类别。演示领域图的用法，

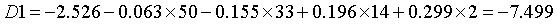
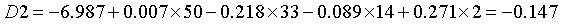
　　从上图可见，该案例显然应当判为第1类，即毛鸢尾花，与实际相一致。如果需同时对一批未知样本给出类别判断，则可以使用save子对话框中的存储功能。

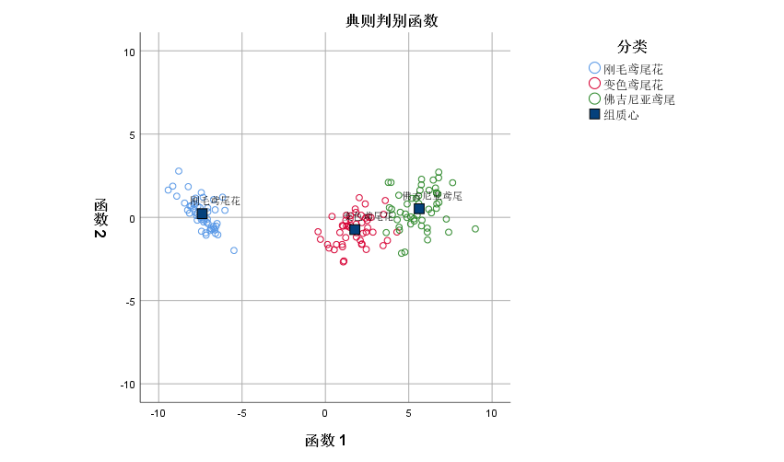
　　从这幅图同样可以看到第1判别轴上3中不同类型的植物区分得很清楚，而在第2判别轴上重合地非常厉害。

1 DISCRIMINANT
2   /GROUPS=spno(1 3)
3   /VARIABLES=slen swid plen pwid
4   /ANALYSIS ALL
5   /PRIORS EQUAL
6   /STATISTICS=RAW
7   /PLOT=COMBINED MAP
8   /CLASSIFY=NONMISSING POOLED.

　　判别效果检验，在【判别分析】的对话框中，点击【分类】，勾选【摘要表】，【继续】，【确定】。

　　运行示例，

分类结果^a
			分类		预测组成员信息						总计
					刚毛鸢尾花		变色鸢尾花		佛吉尼亚鸢尾花
原始	计数	刚毛鸢尾花		50		0		0		50
		变色鸢尾花		0		48		2		50
		佛吉尼亚鸢尾花		0		1		49		50
	%	刚毛鸢尾花		100.0		.0		.0		100.0
		变色鸢尾花		.0		96.0		4.0		100.0
		佛吉尼亚鸢尾花		.0		2.0		98.0		100.0
a. 正确地对 98.0% 个原始已分组个案进行了分类。

　　上表可见，刚毛花全部正确预测，而另两种花则存在错判。（判断率超过41.67%就可）。显然，用本例建立的判别函数进行新样品判别，效果将是令人非常满意。

1 DISCRIMINANT
2   /GROUPS=spno(1 3)
3   /VARIABLES=slen swid plen pwid
4   /ANALYSIS ALL
5   /PRIORS EQUAL
6   /STATISTICS=RAW TABLE
7   /PLOT=COMBINED MAP
8   /CLASSIFY=NONMISSING POOLED.

　　适用条件的判断方法，在【判别分析】的对话框中，点击【统计】，勾选【平均值】、【单变量ANOVA】、【博克斯】，【继续】，【确定】。

运行示例

组平均值的同等检验
	威尔克 Lambda	F	自由度 1	自由度 2	显著性
花萼长	.397	111.847	2	147	.000
花萼宽	.598	49.371	2	147	.000
花瓣长	.059	1179.052	2	147	.000
花瓣宽	.071	960.007	2	147	.000

　　由表中的最后的Sig值可见，很明显各组间存在差异，因此这些变量的判别可能是有作用的。

对数决定因子
分类	秩	对数决定因子
刚毛鸢尾花	4	5.353
变色鸢尾花	4	7.594
佛吉尼亚鸢尾花	4	10.495
汇聚组内	4	8.920
打印的决定因子的秩和自然对数是组协方差矩阵的相应信息。

　　协方差齐性的博克斯检验，从右侧的输出可见组间协方差这一原假设被拒绝，竟然连Fisher给出的判别分析实例都违反这一适用条件，从这一点看出协方差齐性等要求往往是被忽视的。

1 DISCRIMINANT
2   /GROUPS=spno(1 3)
3   /VARIABLES=slen swid plen pwid
4   /ANALYSIS ALL
5   /PRIORS EQUAL
6   /STATISTICS=MEAN STDDEV UNIVF BOXM RAW TABLE
7   /PLOT=COMBINED MAP
8   /CLASSIFY=NONMISSING POOLED.

　　贝叶斯判别分析，同样的实例。SPSS操作，在【判别分析】的对话框中，点击【统计】勾选【费希尔】，【继续】；点击【分类】，勾选【根据组大小计算】，【继续】，【确定】。

　　运行示例，

分类函数系数
	分类
	刚毛鸢尾花	变色鸢尾花	佛吉尼亚鸢尾花
花萼长	1.687	1.101	.865
花萼宽	2.695	1.070	.747
花瓣长	-.880	1.001	1.647
花瓣宽	-2.284	.197	1.695
(常量)	-80.268	-71.196	-103.890
费希尔线性判别函数

　　SPSS认为贝叶斯判别的基本思想，即按判别函数值最大的一组进行归类的思想是Fisher提出来的，因此称该方法为Fisher线性判别函数。

　　刚毛鸢尾花：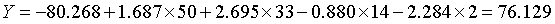

　　变色鸢尾花：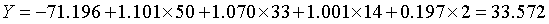

　　弗吉尼亚鸢尾花：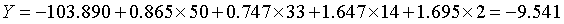

　　下面利用判别式直接计算新观测属于各类的评分，得分最高的一类就是该观测相应的类别。如由于刚毛花判别函数的得分最高，因此和前面一样，判别结果将其归为刚毛花一类，代码：

1 DISCRIMINANT
2   /GROUPS=spno(1 3)
3   /VARIABLES=slen swid plen pwid
4   /ANALYSIS ALL
5   /PRIORS SIZE
6   /STATISTICS=MEAN STDDEV UNIVF BOXM COEFF TABLE
7   /PLOT=COMBINED MAP
8   /CLASSIFY=NONMISSING POOLED.

小结

　　聚类方法的选择：

聚类方法	对记录聚类	对变量聚类	数据量<100	100-1000	>1000	连续变量	指定类别数量
层次聚类	√	√	√√	√ 树状图×		√	√
非层次聚类	√		√	√ 树状图×		√
K-均值聚类法	√		√	√ 树状图×	√	√（可包含离散变量）	√

　　判别分析的使用条件，

　　（1）自变量和因变量的关系符合线性假定。

　　（2）因变量的取值是独立的，且必须是事先就已经确定的。

　　（3）自变量服从多元正态分布。

　　（4）所有自变量在各组件方差齐性，协方差矩阵也相等。

　　（5）所有自变量不存在多重共线性。

　　违背条件的处理方法，

　　（1）当样本的多元正态分布假设不能满足的时候采取的措施和方法：

如果数据的超平面是若干分段结构的时候，采用分段判别分析。
如果数据满足方差齐性和协方差齐性可以采用距离判别分析、经典判别分析、贝叶斯判别分析。（建议使用经典判别分析）
如果数据不满足方差齐性和协方差齐性，则采用经典判别分析、非参数判别分析、距离判别分析。
进行变量变换。

（2）方差齐性和协方差齐性不满足，

增加样本。
采用经典判别分析、非参数判别分析、距离判别分析。

（3）存在多重共线，

增加样本。
采用逐步判别分析。
采用岭判别分析。
对成分进行主成分分析，用因子代替变量进行判别。
通过相关矩阵知识删去共线性的自变量。

（4）当线性假设被违反，

离散型判别分析或混合型判别分析。
K最近邻判别分析或核密度判别分析。
采用二次判别分析。

相关阅读:
ios端点击document，input框不会失去焦点
 只能输入整数和小数
 Array.prototype.slice.call()方法详解（调用方法中的参数截取出来）
jquery自带的显示隐藏功能（有过渡效果）
jquery鼠标事件
 JavaScript的switch循环
 JS获取当前时间
 jquery添加元素
 逻辑非（！）与（&&）或（||）
css玩转文字
原文地址：https://www.cnblogs.com/jianle23/p/12951535.html