优秀的统计学者,首先得具有良好的数学建模素养,再之是具备侦查数据的能力,其次是统计学实验的积累,最后才是统计学知识的储备。时间序列预测是一个非常有趣的课题,能使用时序预测的实际问题几乎涉及我们生活、工作、科研等方方面面。如:天气预报、股市预测、产品推荐、水文预报、计算机技术、空间技术(如:多时相遥感图像数据分析,3S技术)、通讯技术、数据库技术、网络技术、卫生领域等。
时序预测除了使用领域广阔之外,也是统计学入门的一个很好的课题。因为它的工作流程就是一个完整的、有说服力的统计学实验流程,并且对实际数据的处理与预测,可以一窥现实世界的一些规律,特别是它的预测功能,时常给人意外之喜。要按一定的准确率去预测现实世界的某个事物,所用到的数据分析的方法,常常可以根据实际对模型进行修改,对于建模思维的培养是有益处的……总而言之,学习、使用和改进时间预测的过程,充满了乐趣。
不可否认的是时序预测也有其局限性,预测渐进变化或一定时间里的变化,时序预测有其优势。但是,现实世界还有突进变化和不确定性因素。例如,COVID-19的突然性就使得以往的时序预测严重失真。时序预测也叫外推法或历史延伸法,它的基本特点是,假定事物的过去趋势会延伸到未来,换句话说“过去这样,今后也将这样”,预测所依据的数据具有不规则性,忽视市场之间发展的因果关系。因此,我们在使用时序预测前,理应作出一些适用性评估,并且在完成某项预测实验后,理应多多检验,找出模型的适用边界。
综上所述,学会时序预测,有助于我们在统计学领域走得更远。本文分为两个部分,一个部分是对“第五章 非平稳序列的确定性分析”和“第11章 时间序列预测”的阅读笔记。另一个部分是完成一些实验内容。
思考与笔记
Time Series Decomposition由英国统计学家W.M. Persons于1919年在他的论文“商业环境的指标(Indices of Business Conditions)”一文中首次使用。
因素分解方法认为所有的序列波动都可以归纳为受到如下四大类因素的综合影响:
- 长期趋势(Trend)。序列呈现出明显的长期递增或递减的变化趋势。
- 循环波动(Circle)。序列呈现出从低到高再由高到低的反复循环波动。循环周期可长可短,不一定是固定的。
- 季节性变化(Season)。序列呈现出和季节变化相关的稳定周期波动。
- 随机波动(Immediate)。除了长期趋势、循环波动和季节性变化之外,其他不能用确定性因素解释的序列波动,都属于随机波动。
统计学家在进行确定性时间序列分析时,假定序列会受到这四个因素中的全部或部分的影响,导致序列呈现出不同的波动特征。换言之,任何一个时间序列都可以用这四个因素的某个函数进行拟合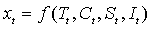 常用模型:
常用模型:
加法模型: ;
;
乘法模型: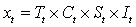 。
。
如果观察时期不是足够长,那么循环因素和趋势因素的影响很难准确区分。比如很多经济或社会现象确实有“上行——峰顶——下行——谷底”周而复始的循环周期。但是这个周期通常很长而且周期长度不是固定的。比如太阳黑子序列,就有9-13年长度不等的周期。在经济学领域更是如此。1913年美国经济学家韦斯利.米歇尔出版了《经济周期》一书,他提出经济周期的持续时间从超过1年到10年或12年不等,它们会重复发生,但不定期。后来不同的经济学家研究不同的经济问题,一再证明经济周期的存在和周期的不确定,比如基钦周期(平均周期长度为40个月左右),朱格拉周期(平均周期长度为10年左右),库兹涅茨周期)平均长度为20年左右),康德拉季耶夫周期(平均周期长度为53.3年)。
如果观察值序列不是足够长,没有包含几个周期的话,那么周期的一部分会和趋势重合,无法准确完整地提取周期影响。
有些社会现象和经济现象显示出某些特殊日期是一个很显著的影响因素,但是在传统因素分解模型中,它却没有被纳入研究。比如研究股票交易序列,成交量、开盘价、收盘价会明显受到交易日的影响,同一只股票每周一和每周五的波动情况可能有显著的不同。超市销售情况更是明显受到特殊日期的影响,工作日、周末、重大假日的销售特征相差很大。春节、端午节、中秋节、儿童节、圣诞节、双11等不同的节日对零售业、旅游业、运输业、电商等多个行业都有显著影响。
如果观察时期不是足够长,人们将循环因素(Circle)改为特殊交易日因素(Day)。新的四大因素为:趋势(T),季节(S),交易日(D)和随机波动(I)。
加法模型: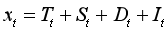 ;
;
乘法模型: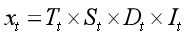 ;
;
伪加法模型: ;
;
对数加法模型: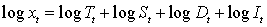 。
。
确定时序分析的目的,一是克服其他因素的干扰,单纯测度出某个确定性因素(诸如季节,趋势,交易日)对序列的影响。二是根据序列呈现的确定性特征,选择适当的方法对序列进行综合预测。时序预测的一般流程如下:

图1 时序预测流程
图1所说的“时间序列图”,一般指推移图(又称趋势图)。它是以时间为横轴,观察变量为纵轴,用以反映时间与数量之间的关系,观察变量的变化发展趋势及偏差的统计图。推移图一般是以折线图形式表现,横轴时间可以是小时、日、月、年等,各时间点应连续不间断(如果有缺失值,可适当插值),纵轴观察变量可以是绝对值、平均值、发生率等。其所提供的信息有:趋势、震荡(过程突然改变与跳动)、混合(不同总体数据的表现,由靠近中心线的点判断)、群集(数据点聚集在图中的一个区域)、循环型周期(季节性等)。

图2 四种时序图
图1所示的预测方法的使用经验指导如下:

图3 预测方法的使用经验指导
预测方法的评估:一种预测方法的好坏取决于预测误差的大小,预测误差是预测值与实际值的差距。度量方法有平均误差(mean error)、平均绝对误差(mean absolute deviation)、均方误差(mean square error)、平均百分比误差(mean percentage error)和平均绝对百分比误差(mean absolute percentage error),较为常用的是均方误差 (MSE),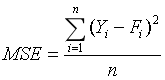 。
。
图1所提到预测方法的介绍如下,所使用的数据如表:
表1 例子的原始数据


图4 原始数据的折线图
平稳序列的预测方法
平稳序列(stationary series):不含有趋势的序列,其波动主要是随机成分所致,序列的平均值不随着时间的推移而变对不断获得的实际数据和原预测数据给以加权平均,使预测结果更接近于实际情况的预测方法,又称光滑法或递推修正法。平稳序列的预测方法有简单平均(simple average)法、移动平均(moving average)法、简单指数平滑(simple exponential smoothing)法、Box-Jenkins方法(ARIMA模型)等。
移动平均预测
选择一定长度的移动间隔,对序列逐期移动求得平均数作为下一期的预测值,将最近k期数据平均作为下一期的预测值,设移动间隔为k (1<k<t),则t+1期的移动平均预测值为 ,预测误差用MSE来衡量,MSE=误差平方和/误差个数。
,预测误差用MSE来衡量,MSE=误差平方和/误差个数。
移动平均的特点:将每个观测值都给予相同的权数,只使用最近期的数据;在每次计算移动平均值时,移动的间隔都为k;主要适合对较为平稳的序列进行预测;对于同一个时间序列,采用不同的移动步长预测的准确性是不同的,选择移动步长时,可通过试验的办法,选择一个使均方误差达到最小的移动步长。
简单指数平滑预测
合于平稳序列(没有趋势和季节变动的序列),是对过去的观测值加权平均进行预测的一种方法。观测值时间越远,其权数也跟着呈现指数的下降,因而称为指数平滑。t+1的预测值是t期观测值与t期平滑值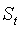 的线性组合,其预测模型为
的线性组合,其预测模型为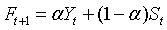 ,
,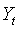 为第t期的实际观测值,
为第t期的实际观测值,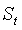 为第t期的预测值,
为第t期的预测值, 为平滑系数, (0 <
为平滑系数, (0 <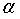 <1)。
<1)。 。
。
不同的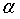 会对预测结果产生不同的影响。当时间序列有较大的随机波动时,宜选较小的
会对预测结果产生不同的影响。当时间序列有较大的随机波动时,宜选较小的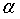 ,注重于近期的实际值时,宜选较大的
,注重于近期的实际值时,宜选较大的 。
。
选择 时,还应考虑预测误差。误差均方来衡量预测误差的大小确定
时,还应考虑预测误差。误差均方来衡量预测误差的大小确定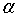 时,可选择几个进行预测,然后找出预测误差最小的作为最后的值。
时,可选择几个进行预测,然后找出预测误差最小的作为最后的值。
【例题1】根据表1中的棉花产量数据,分别取移动间隔k=3和 =0.3进行移动平均和指数平滑预测,计算出预测误差,并将原序列和预测后的序列绘制成图形进行比较。分析截图:
=0.3进行移动平均和指数平滑预测,计算出预测误差,并将原序列和预测后的序列绘制成图形进行比较。分析截图:
表2 使用Excel做移动平均和指数平滑预测
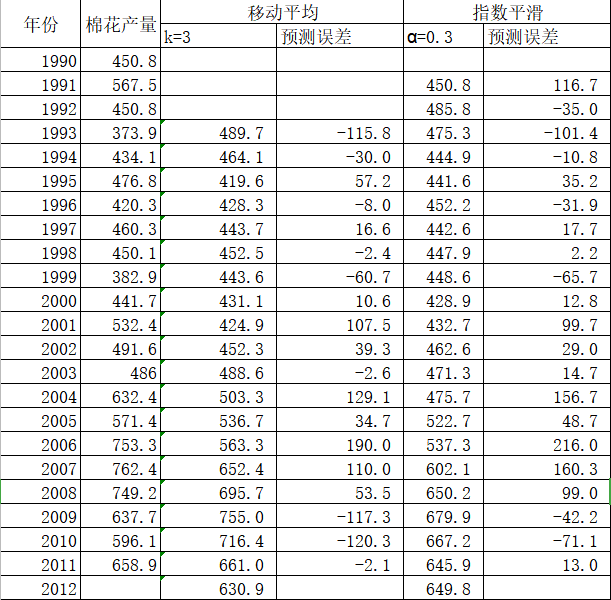

图5 例1结果
趋势序列的预测方法
线性趋势预测
线性趋势:是时间序列按一个固定的常数(不变的斜率)增长或下降。拟合一条线性趋势方程进行预测。 。t——时间变量,
。t——时间变量,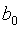 ——趋势线在Y轴上的截距,
——趋势线在Y轴上的截距,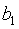 ——斜率,表示时间t变动一个单位时观测值的平均变动量。
——斜率,表示时间t变动一个单位时观测值的平均变动量。
【例题2】根据表1中啤酒产量数据,用直线趋势方程预测2012年的啤酒产量,并给出各年的预测值和预测误差,将实际值和预测值绘制成图形进行比较。
表3 得到线性回归需要的参数

表4 Excel线性趋势预测
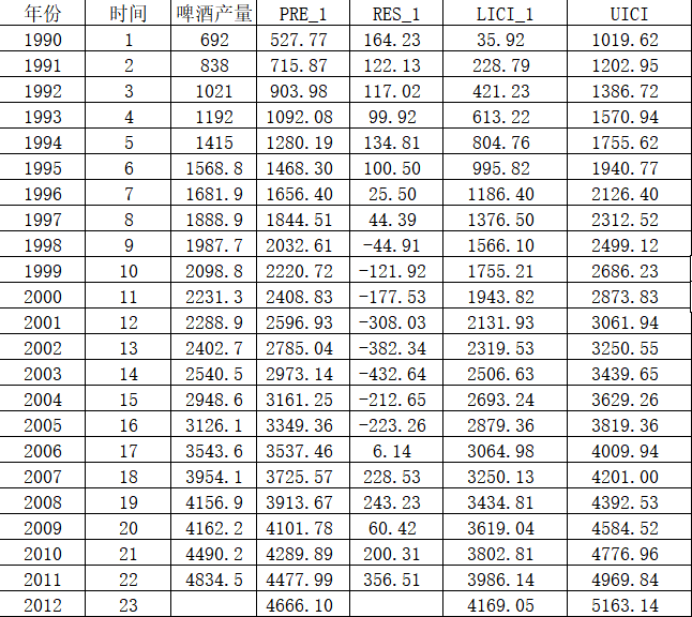
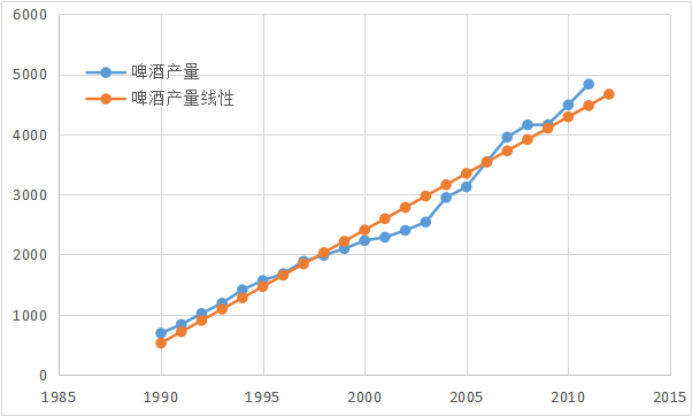
图6 例2结果
Holt指数平滑预测
在简单指数平滑中,实际上是用期的平滑值作为期的预测值,它适合于较平稳的序列。当时间序列存在趋势时,简单指数平滑的预测结果总是滞后于实际值。Holt指数平滑预测模型,一般简称为Holt模型(Holt’s model),适合于含有趋势成分(或有一定的周期成分)序列的预测。Holt模型使用两个参数(平滑系数) 和
和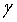 (取值均在0和1之间)和以下三个方程:
(取值均在0和1之间)和以下三个方程:


Holt模型中初始值的确定,

【例题3】沿用例2。用Holt指数平滑模型预测2012年的啤酒产量,并将实际值和预测值绘制成图形进行比较。
表5 SPSS的Holt指数平滑预测
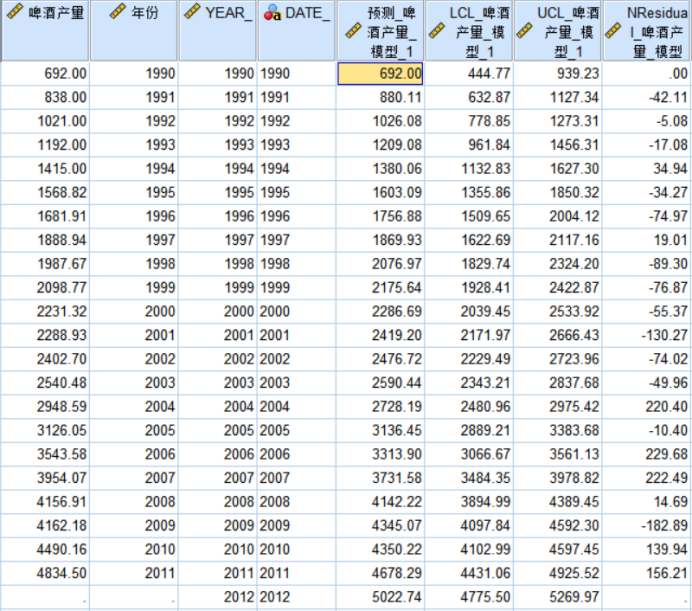

图7 例3结果
非线性预测
指数曲线,时间序列以几何级数递增或递减。一般形式为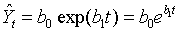 为的待定系数,exp表示自然对数ln的反函数,e=2.71828182845904,可线性化后使用最小二乘法,可直接使用SPSS。
为的待定系数,exp表示自然对数ln的反函数,e=2.71828182845904,可线性化后使用最小二乘法,可直接使用SPSS。
多阶曲线,有些现象的变化形态比较复杂,它们不是按照某种固定的形态变化,而是有升有降,在变化过程中可能有几个拐点。这时就需要拟合多项式函数。当只有一个拐点时,可以拟合二阶曲线,即抛物线;当有两个拐点时,需要拟合三阶曲线;当有k-1个拐点时,需要拟合k阶曲线。k阶曲线函数的一般形式为 。可线性化后,根据最小二乘法
。可线性化后,根据最小二乘法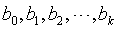 ,使用SPSS的【Analyze】→【Regression – Curve Estimation】→【Models】→【Cubic】得到。
,使用SPSS的【Analyze】→【Regression – Curve Estimation】→【Models】→【Cubic】得到。
【例4】根据表1中的轿车产量数据,用指数曲线预测2012年的轿车产量,并计算出各期的预测值和预测误差,将实际值和预测值绘制成图形进行比较。
表6 SPSS指数曲线预测
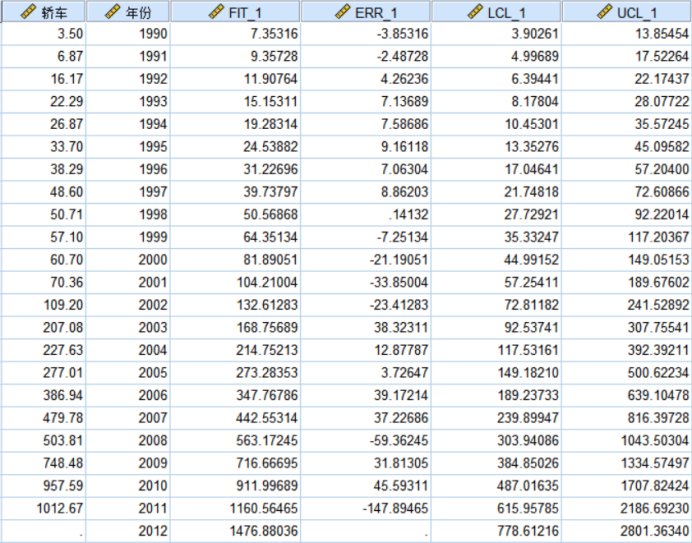
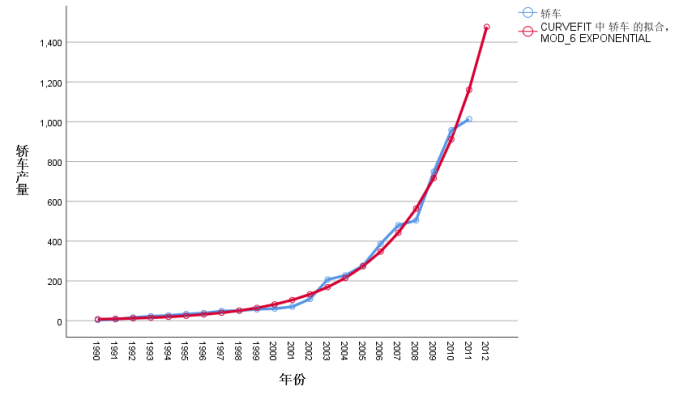
图8 例4结果
【例题5】根据表1中的金属切削机床产量数据,拟合适当的趋势曲线,预测2006年的金属切削机床产量,并计算出各期的预测值和预测误差,将实际值和预测值绘制成图形进行比较。
表7 SPSS多阶曲线预测
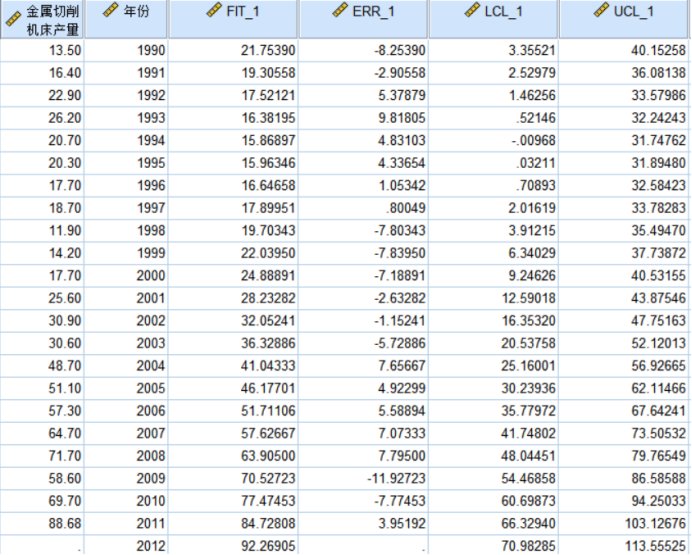
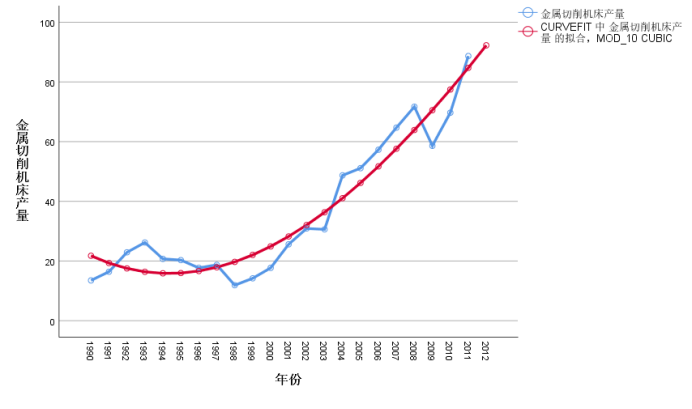
图9 例4结果
多成分序列的预测方法
Winters指数平滑预测
简单指数平滑模型适合于对平稳序列(没有趋势和季节成分)的预测;Holt指数平滑模型适合于含有趋势成分但不含季节成分序列的预测。如果时间序列中既含有趋势成分又含有季节成分,则可以使用Winter指数平滑模型进行预测。要求数据是按季度或月份收集的,而且至少需要4年(4个季节周期长度)以上的数据。Winter指数平滑模型包含三个平滑参数即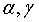 和
和 (取值均在0和1之间)和以下四个方程,平滑值:
(取值均在0和1之间)和以下四个方程,平滑值: ,趋势项更新:
,趋势项更新: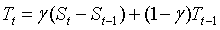 ,季节项更新:
,季节项更新: ,K期预测值:
,K期预测值: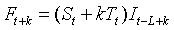 。
。

表8 winter指数平滑预测
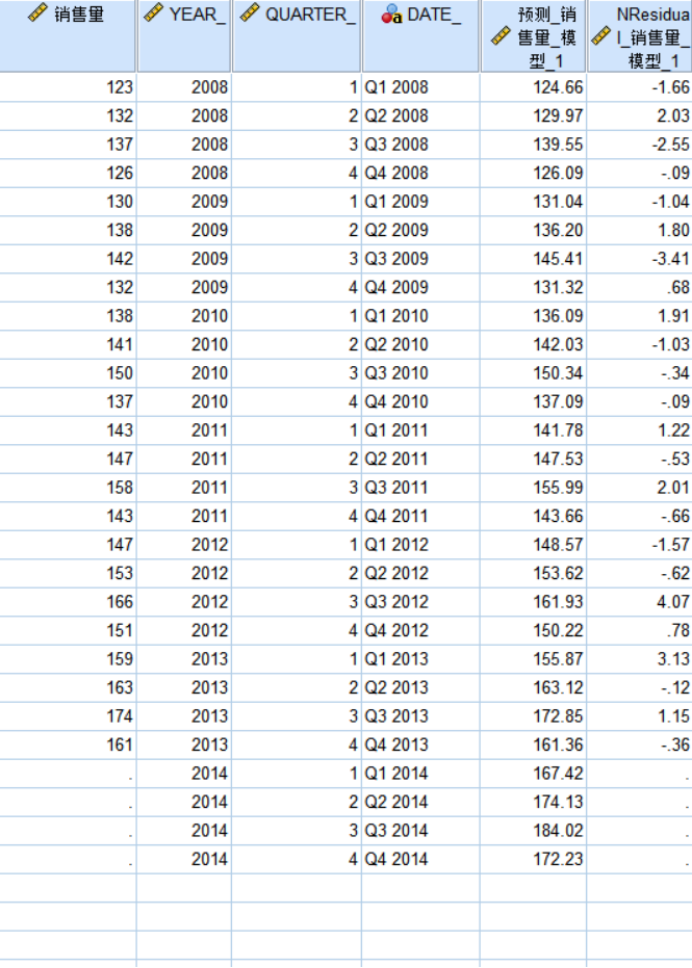
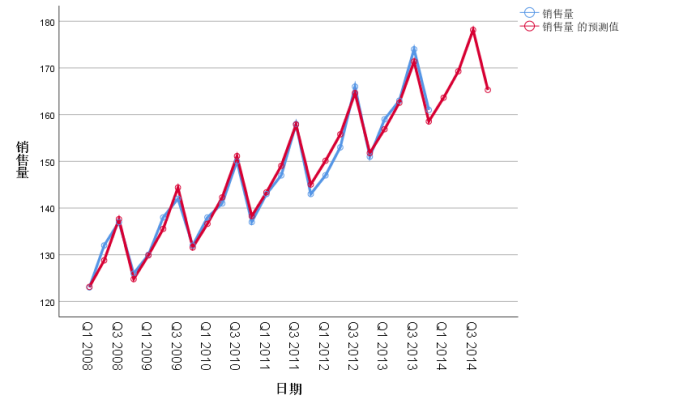
图10 例5结果
引入季节哑变量的多元回归预测
用虚拟变量表示季节的多元回归预测方法,若数据是按季度记录的,需要引入3个虚拟变量(一季度作为参照水平);按月记录的,则需要引入11个虚拟变量
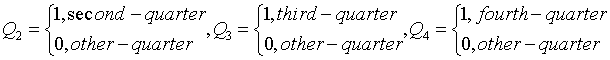
季度数据的季节性多元回归模型可表示为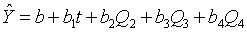 。
。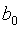 ——时间序列的平均值。
——时间序列的平均值。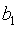 ——趋势成分的系数,表示趋势给时间序列带来的影响值。
——趋势成分的系数,表示趋势给时间序列带来的影响值。 ——3个季度的虚拟变量。
——3个季度的虚拟变量。 ——每一个季度与参照的第一季度的平均差值。
——每一个季度与参照的第一季度的平均差值。
【例6】下表是一家饮料生产企业2008—2013年各季度的销售量数据。用分解预测法预测2014年各季度的啤酒销售量,并计算出各期的预测值和预测误差,将实际值和预测值绘制成图形进行比较。
表9 SPSS季节性哑变量回归预测
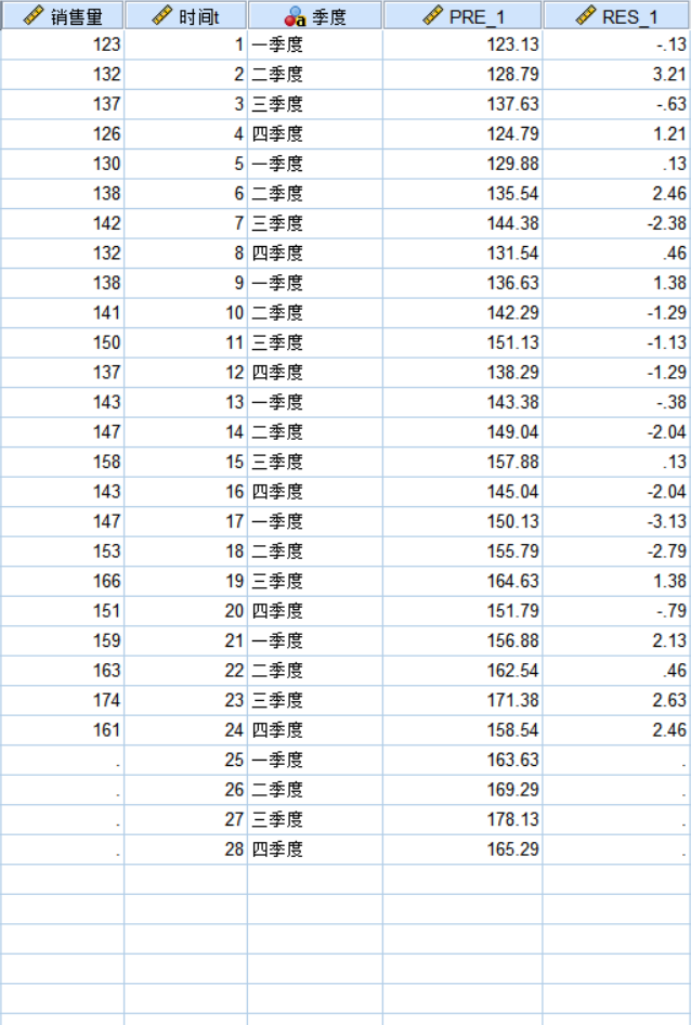

图11 例6结果
分解预测
分解(decomposition)预测是适合于含有趋势、季节、循环多种成分序列预测的一种古典方法,仍得到广泛应用,因为该方法相对来说容易理解,结果易于解释,在很多情况下能给出很好的预测结果。预测步骤:确定并分离季节成分,计算季节指数,以确定时间序列中的季节成分,将季节成分从时间序列中分离出去,即用每一个观测值除以相应的季节指数,以消除季节性;对消除季节成分的序列建立线性预测模型进行预测,计算出最后的预测值,用预测值乘以相应的季节指数,得到最终的预测值。
计算季节指数:
1.以其平均数等于100%为条件而构成的反映季节变动的值;
2.表示某一月份或季度的数值占全年平均数值的大小;
3.如果现象的发展没有季节变动,则各期的季节指数应等于100%;
4.季节变动的程度是根据各季节指数与其平均数(100%)的偏差程度来测定。
季节指数计算步骤:
1.计算移动平均值(季度数据采用4项移动平均,月份数据采用12项移动平均),并将其结果进行“中心化”处理(再一次2项移动平均)
2.计算移动平均的比值,也称为季节比率,将序列的各观测值除以相应的中心化移动平均值,然后再计算出各比值的季度(或月份)平均值,即季节指数。
3.季节指数调整,各季节指数的平均数应等于1或100%,若根据第2步计算的季节比率的平均值不等于1时,则需要进行调整具体方法是:将第2步计算的每个季节比率的平均值除以它们的总平均值 。
分离季节成分:将原时间序列除以相应的季节指数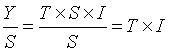 。季节因素分离后的序列反映了在没有季节因素影响的情况下时间序列的变化形态。
。季节因素分离后的序列反映了在没有季节因素影响的情况下时间序列的变化形态。
【例题7】下表是一家饮料生产企业2008—2013年各季度的销售量数据。用分解预测法预测2014年各季度的啤酒销售量,并计算出各期的预测值和预测误差,将实际值和预测值绘制成图形进行比较。
表10 SPSS分解预测


图12 例7结果

图13 例7结果
X-12-ARIMA模型
第一步:根据序列的特点,考察序列值是否会受到某些确定性的异常值的影响X-12-ARIMA模型经常考察的一些异常因素包括月度长度、季度长度、固定季节因素、工作日因素、交易日因素、闰年因素、特殊节假日(春节、十一假期、双十一购物节)等。如果序列有可能受到这些因素的显著影响,则将这些因素作为自变量,序列作为因变量,建立回归模型。如果回归模型显著成立,则说明该影响因素对序列有显著稳定的影响,
第二步:对回归残差序列(如果回归方程显著)或原序列(如果回归方程不显著)拟合ARIMA模型。
第三步:构建X-11模型。依然是3阶段10步迭代运算。但是期间系统会使用第二步拟合出来的ARIMA模型,自动向前或向后做序列预测,根据需要扩充数据,以得到更准确的因素分解结果。
使用SPSS和Excel预测
具体过程看《SPSS时间序列预测》和《表格与时间序列预测》。
【资料】
- 第五章PPT,
- 第11章PPT,
- 推移图。
- 《时间序列分析在测量领域的应用》