实验目的:
1、学会使用SPSS的简单操作。
2、掌握回归分析。
实验内容:
1.相关分析。线性回归相关关系指一一对应的确定关系。设有两个变量 x 和 y ,变量 y 随变量 x 一起变化,并完全依赖于 x ,当变量 x 取某个数值时, y 依确定的关系取相应的值,则称 y 是 x 的函数,记为 y = f (x),其中 x 称为自变量,y 称为因变量。且各观测点落在一条线上 。
2.回归分析,重点考察考察一个特定的变量(因变量),而把其他变量(自变量)看作是影响这一变量的因素,并通过适当的数学模型将变量间的关系表达出来利用样本数据建立模型的估计方程对模型进行显著性检验进而通过一个或几个自变量的取值来估计或预测因变量的取值。
3.逐步回归,将向前选择和向后剔除两种方法结合起来筛选自变量。在增加了一个自变量后,它会对模型中所有的变量进行考察,看看有没有可能剔除某个自变量。如果在增加了一个自变量后,前面增加的某个自变量对模型的贡献变得不显著,这个变量就会被剔除。按照方法不停地增加变量并考虑剔除以前增加的变量的可能性,直至增加变量已经不能导致SSE显著减少在前面步骤中增加的自变量在后面的步骤中有可能被剔除,而在前面步骤中剔除的自变量在后面的步骤中也可能重新进入到模型中。
4.哑变量回归,也称虚拟变量。用数字代码表示的定性自变量。哑变量可有不同的水平。哑变量的取值为0,1。
实验步骤:
- 相关分析SPSS操作,【分析】→【相关-双变量】,将各变量选入【变量】。

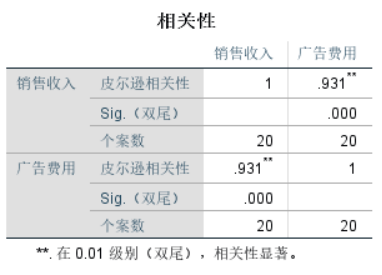

1 CORRELATIONS 2 /VARIABLES=销售收入 广告费用 3 /PRINT=TWOTAIL NOSIG 4 /MISSING=PAIRWISE.
2.回归分析SPSS操作,【分析】→【回归-线性】,将因变量选入【因变量】,将自变量选入【自变量】。需要预测时,【保存】→【预测值】,选中【未标准化】→【预测区间】,选中【均值】→【单值】→【置信区间】,选择置信水平。需要分析残差时,【保存】→【残差】,选中【未标准化】,选中标准化。需要输出标准残差的直方图和正态概率图时,【绘图】→【标准化残差图】,选中【直方图】,选中【正态概率图】。
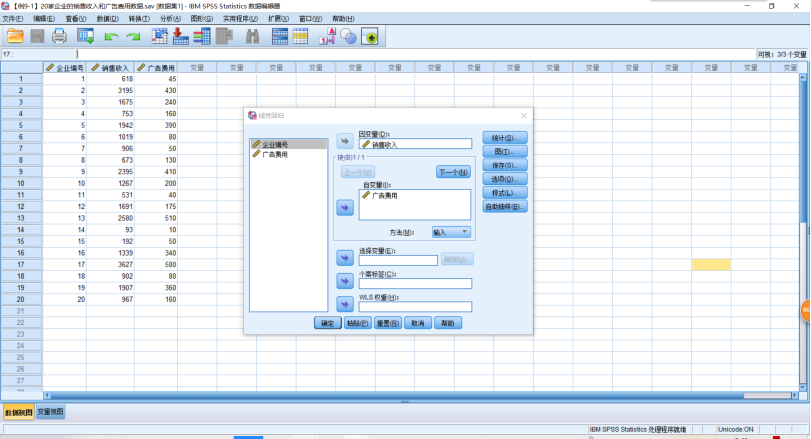
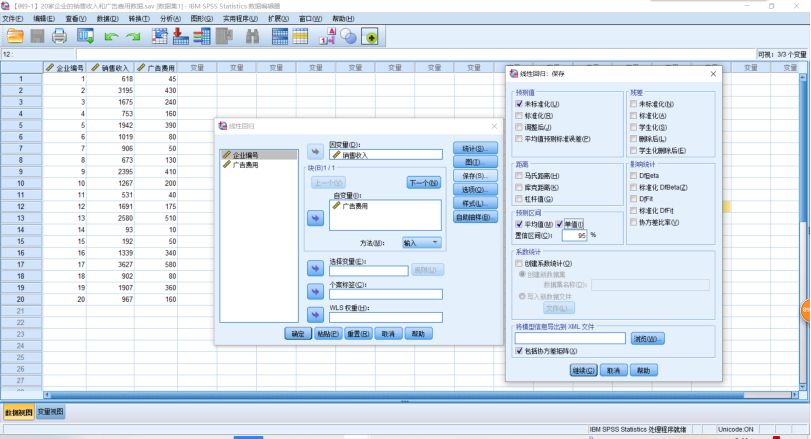
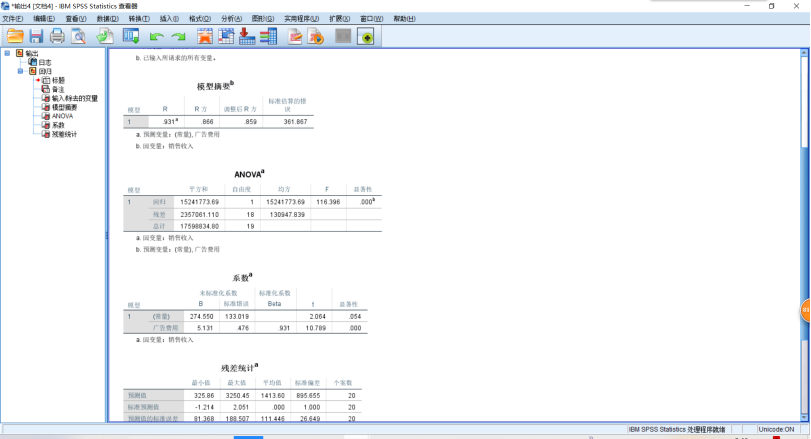

1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS R ANOVA 4 /CRITERIA=PIN(.05) POUT(.10) CIN(95) 5 /NOORIGIN 6 /DEPENDENT 销售收入 7 /METHOD=ENTER 广告费用 8 /SAVE PRED MCIN ICIN.


1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS R ANOVA 4 /CRITERIA=PIN(.05) POUT(.10) CIN(95) 5 /NOORIGIN 6 /DEPENDENT 销售收入 7 /METHOD=ENTER 广告费用 8 /SAVE MCIN RESID ZRESID.

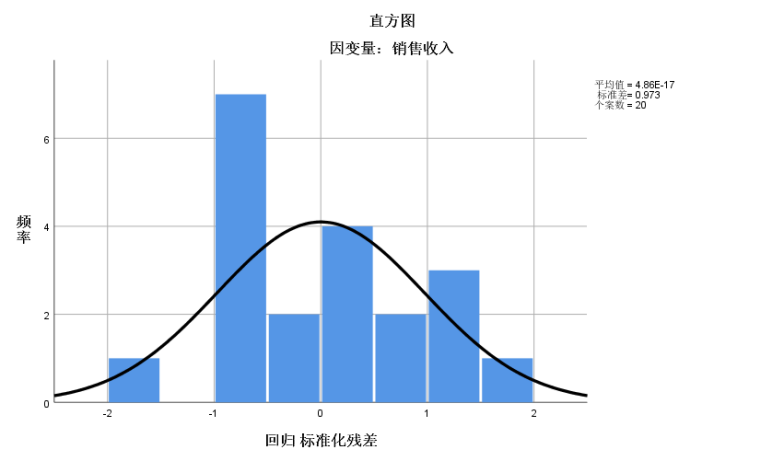
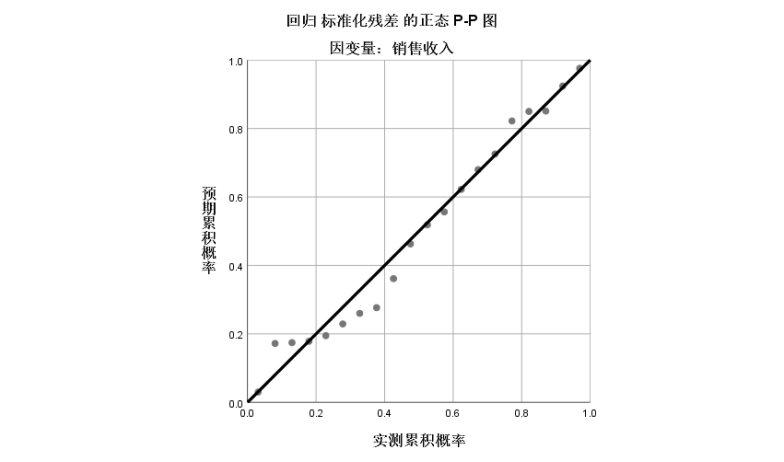

1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS R ANOVA 4 /CRITERIA=PIN(.05) POUT(.10) 5 /NOORIGIN 6 /DEPENDENT 销售收入 7 /METHOD=ENTER 广告费用 8 /RESIDUALS HISTOGRAM(ZRESID) NORMPROB(ZRESID).
3.逐步回归SPSS操作,【分析】→【回归-线性】,将因变量选入【因变量】,将自变量选入【自变量】,【方法】→【步进】,【选项】→【步进方法标准】,选中【使用F的概率】,【进入】输入增加变量显著度,【删除】输入剔除变量的显著度,【继续】。需要预测时,【保存】→【预测值】,选中【均值】【单值】【置信区间】,选择置信水平。需要分析残差时,【保存】→【残差】,选中【未标准化】,选中【标准化】。
|
输入/除去的变量a |
|||
|
模型 |
输入的变量 |
除去的变量 |
方法 |
|
1 |
累计应收贷款 |
. |
步进(条件:要输入的 F 的概率 <= .050,要除去的 F 的概率 >= .100)。 |
|
2 |
贷款项目个数 |
. |
步进(条件:要输入的 F 的概率 <= .050,要除去的 F 的概率 >= .100)。 |
|
a. 因变量:不良贷款 |
|||
|
模型摘要 |
||||
|
模型 |
R |
R 方 |
调整后 R 方 |
标准估算的错误 |
|
1 |
.732a |
.535 |
.515 |
2.5139 |
|
2 |
.805b |
.648 |
.615 |
2.2381 |
|
a. 预测变量:(常量), 累计应收贷款 |
||||
|
b. 预测变量:(常量), 累计应收贷款, 贷款项目个数 |
||||

|
ANOVAa |
||||||
|
模型 |
平方和 |
自由度 |
均方 |
F |
显著性 |
|
|
1 |
回归 |
167.299 |
1 |
167.299 |
26.473 |
.000b |
|
残差 |
145.351 |
23 |
6.320 |
|||
|
总计 |
312.650 |
24 |
||||
|
2 |
回归 |
202.450 |
2 |
101.225 |
20.208 |
.000c |
|
残差 |
110.200 |
22 |
5.009 |
|||
|
总计 |
312.650 |
24 |
||||
|
a. 因变量:不良贷款 |
||||||
|
b. 预测变量:(常量), 累计应收贷款 |
||||||
|
c. 预测变量:(常量), 累计应收贷款, 贷款项目个数 |
||||||

1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS R ANOVA 4 /CRITERIA=PIN(.05) POUT(.10) 5 /NOORIGIN 6 /DEPENDENT 不良贷款 7 /METHOD=STEPWISE 累计应收贷款 贷款项目个数 固定资产投资.


1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS R ANOVA 4 /CRITERIA=PIN(.05) POUT(.10) CIN(95) 5 /NOORIGIN 6 /DEPENDENT 不良贷款 7 /METHOD=STEPWISE 累计应收贷款 贷款项目个数 固定资产投资 8 /SAVE PRED MCIN ICIN.

1 REGRESSION 2 /MISSING LISTWISE 3 /STATISTICS COEFF OUTS R ANOVA 4 /CRITERIA=PIN(.05) POUT(.10) CIN(95) 5 /NOORIGIN 6 /DEPENDENT 不良贷款 7 /METHOD=STEPWISE 累计应收贷款 贷款项目个数 固定资产投资 8 /SAVE MCIN RESID ZRESID.
4.哑变量分析SPSS操作:【分析】→【一般线性模型】→【单变量】,将因变量选入【因变量】,将哑变量选入【固定因子】,将数字变量选入【协变量】,【模型】→【构建项】→【单变量】,将哑变量选入【模型】,将数字自变量选入【模型】,【构建项】→【主效应】→【继续】→【选项】→【显示】→【参数估计值】。

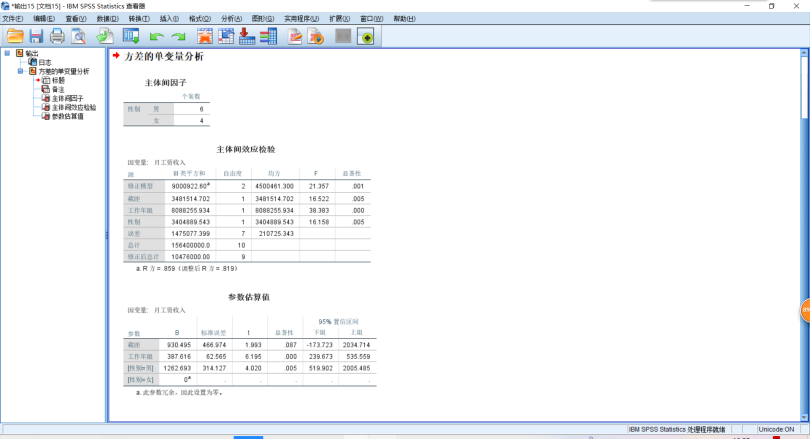

1 UNIANOVA 月工资收入 BY 性别 WITH 工作年限 2 /METHOD=SSTYPE(3) 3 /INTERCEPT=INCLUDE 4 /PRINT PARAMETER 5 /CRITERIA=ALPHA(.05) 6 /DESIGN=工作年限 性别.
小结:
线性分析和回归具有密切的联系,多重线性回归模型可以使用向前法、向后法、逐步法等多种回归分析方法来协助进行变量筛选,但是自动筛选不能完全替代人工筛选。回归模型有着自己严格的适用条件,在拟合需要不断进行这些适用条件的判断。标准的回归模型步骤应当包括如下内容:作出散点图,观察变量间的趋势;考察数据的分布,进行必要的预处理;进行直线回归线性,建立基本模型;进行残差分析;进行强影响点的诊断及多重共线问题到判断。下一步应当做就是结合专业实际,将分析结果运用到现实中,来看看结果有无实用价值,以及是否存在应用中的其他问题。
