线性规划问题（二）

实验目的：

　　通过实验，掌握线性规划问题的求解过程。建立模型后，可以用Lingo软件求解，也可以用MATLAB软件求解，了解MATLAB和Lingo在求解线性规划问题中的不同之处。

实验要求：

　　要有建模过程。

实验内容：　　

　　（1）背包问题，某人打算外出旅游并登山, 路程比较远, 途中要坐火车和飞机, 考虑要带许多必要的旅游和生活用品, 如照相机, 摄像机, 食品, 衣服, 雨具, 书籍等, 共8件物品, 重量分别为1, 3, 4,3, 3, 1, 5, 10 (千克), 而受航空行李重量限制以及个人体力所限, 能带的行李总重量为15 千克, 8件物品的总重量超过了15千克, 需要裁减, 该旅行者为了决策带哪些物品, 对这些物品的重要性进行了量化, 价值分别为2, 9, 3, 8, 10, 6, 4, 10, 试建立该问题的数学模型.

　　（2）配料问题，某疗养院营养师要为某类病人拟订本周蔬菜类菜单, 当前可供选择的蔬菜品种, 价格和营养成分含量, 以及病人所需养分的最低数量见表1所示. 病人每周需14份蔬菜, 为了口味的原因, 规定一周内的卷心菜不多于2份, 胡萝卜不多于3份, 其他蔬菜不多于4份且至少一份. 在满足要求的前提下, 制订费用最少的一周菜单方案.

　　

　　（3）某航空公司每天有三个航班服务于A, B, C, H四个城市,其中城市H是可供转机使用的, 三个航班的出发地-目的地分别为AH, HB, HC,可搭乘旅客的最大数量分别为120人, 100人, 110人, 机票的价格分头等舱和经济舱两类. 经过市场调查, 公司销售部得到了每天旅客的相关信息, 见表1. 该公司应该在每条航线上分别分配多少头等舱和经济舱的机票?

　　

 实验步骤：

　　

 　　使用Lingo求解，

MODEL:
SETS:
WP/W1..W8/:A,C,X;
ENDSETS
DATA:
A=1,3,4,3,3,1,5,10;
C=2,9,3,8,10,6,4,10;
ENDDATA
MAX=@SUM(WP(I):C(I)*X(I));
@SUM(WP(I):A(I)*X(I))<=15;
@FOR(WP(I):@BIN(X(I)));
END

　　

 　　解得，该人带1~6号物品，价值达到38。

　　使用贪心算法MATLAB程序，求得，

function y=beibao(product,weight,value)
fprintf('请输入数据(product,weight,value):
');
product=input('product=');
weight=input('weigth=');
value=input('value=');
Total_value=0;
Total_weight=15;
j=1;
len=length(product);
%chanpin_N=zeros(len);
%chanpin_W=zeros(len);
%chanpin_V=zeros(len);
for i=1:len
    Total_value=Total_value+value(i);
    Total_weight=Total_weight-weight(i);
    if Total_weight<0
        Total_value=Total_value-value(i);
        Total_weight=Total_weight+weight(i);
    else
        chanpin_N(j)=product(i);
        chanpin_W(j)=weight(i);
        chanpin_V(j)=value(i);
        j=j+1;
    end
end
disp('输出对应装入背包的产品号')
chanpin_N
disp('输出装入产品后背包总重量')
sum(chanpin_W)
disp('输出装入产品后背包总重量')
sum(chanpin_V)
end

　　

 　　使用Lingo求解，

model:
sets:
r/1..6/:a,x;
l/1..5/:b;
links(r,l):c;
endsets
data:
a=2.1,1.0,1.8,1.2,2.0,1.2;
b=6,125,12500,345,5;
c=0.45,20,415,22,0.3,
0.45,28,4065,5,0.35,
0.65,40,850,43,0.6,
0.4,25,75,27,0.2,
0.5,26,76,48,0.4,
0.5,75,235,8,0.6;
enddata
min=@sum(r(I):a(I)*x(I));
0<x(1);x(1)<4;
0<x(3);x(3)<4;
0<x(5);x(5)<4;
0<x(6);x(6)<4;
1<x(2);x(2)<3;
1<x(4);x(4)<2;
@sum(r(I):x(I))=14;
@for(l(J):@sum(r(I):c(I,J)*x(I))>b(J));
@for(r(I):@gin(x(I)));
end

　　

 　　解得：购买3份胡萝卜，4份花菜，2份卷心菜，2份芹菜，3份土豆所花费用20.2元最少。

 　　使用Lingo求解，

MODEL: 
TITLE 机票销售计划; 
SETS:     
    route /AH,AB,AC,HB,HC/:a,b,p,q,x,y; 
ENDSETS 
DATA: 
a p b q= 
    33 190 56 90 
    24 244 43 193 
    12 261 67 199 
    44 140 69 80 
    16 186 17 103 ; 
c1 c2 c3 = 120 100 110; 
ENDDATA 
[obj] Max = @SUM(route: p*x+q*y ); 
[AH] @SUM(route(i)|i#ne#4#and#i#ne#5:x(i)+y(i)) < c1; 
[HB] @SUM(route(i)|i#eq#2#or#i#eq#4:x(i)+y(i))  < c2; 
[HC] @SUM(route(i)|i#eq#3#or#i#eq#5:x(i)+y(i))  < c3; 
@FOR(route: @bnd(0,x,a);@bnd(0,y,b) ); 
END

　　

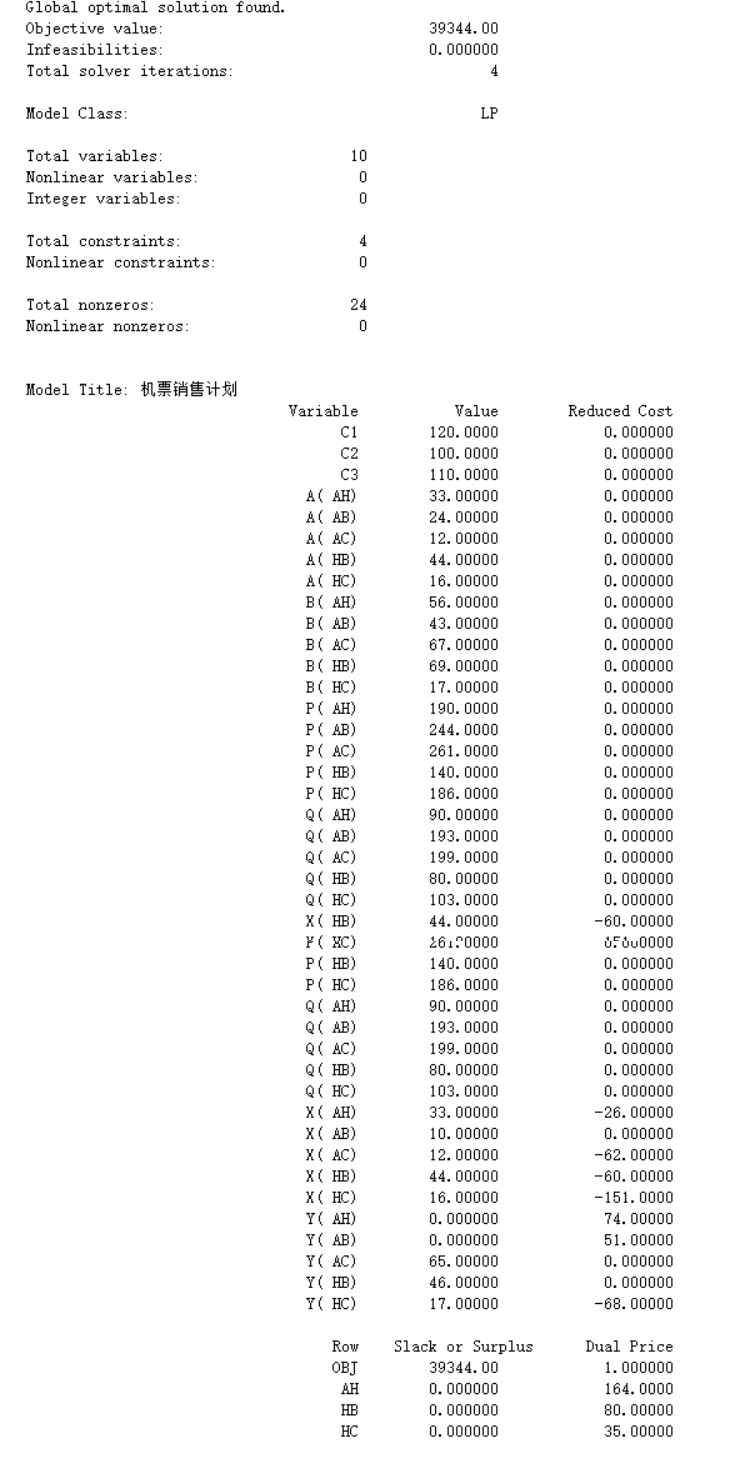
 　　解得，在AH航线33张头等舱，0张经济舱；AB航线10张头等舱，0张经济舱；AC航线12张头等舱，65张经济舱；HB航线44张头等舱，46张经济舱；HC航线103张头等舱，17张经济舱。当时，最优解中AB路线路上的头等舱需求并没有全部满足。

 

小结：

　　对于上述的三个问题，使用Lingo求解更为简单。在使用MATLAB自带的linprog()或者intlinprog()函数，都遇到了问题，总会出现Problem is unbounded.只能退而求其次，使用贪心算法或者动态规划求解了。所以，在解这一类题目，Lingo较之MATLAB更为友好。