topcoder srm 570 div1

problem1 link

找到周期，每个周期的增量是相同的．

problem2 link

对于分给某一个公司的有$c$个联通分量，其中$k$个联通分量只有１个节点，$c$个联通分量一共有$x$个节点．首先，对于那些节点大于１的联通分量($c-k$个)，将这些连接在一起需要$c-k-1$条边，耗费了$2(c-k-1)$个节点．还有$x-k-2(c-k-1)$个节点可以用来连接那些只有１个节点的联通分量，分两种情况：

（１）$k leq x-k-2(c-k-1)$.这时候不需要额外的代价．

（２）$k>x-k-2(c-k-1)$．这时候，需要代价为$k-(x-k-2(c-k-1))=2c+2-x$

可以看出与$k$无关．那么可以计算出选出$c$个联通分量恰好有$x$个节点的方案数．由于对称，最后乘以２再除以总的方案数$2^{n}$就是答案．

problem3 link

第一步，将格子进行黑白染色：

第二步，黑白染色之后，格子就分成了两类，蓝色和绿色．每个格子向相邻的格子连边．新增源点汇点．源点向绿色格子连边，流量为２，蓝色格子向汇点连边，流量为２．如果最大流等于$2n$($n$为非W节点的个数)，那么存在一种方案连接所有格子：

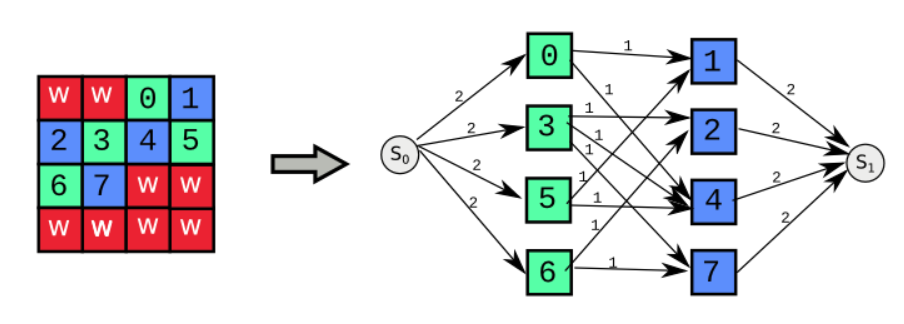
 第三步，考虑是否可以满足所有有效格子里都是弯曲的形状，那么进入一个绿色格子和从这个绿色格子出去的一定是一个横着进来一个竖着出去．所以将每个格子拆分成两个，一个横着的，一个竖着的．横着的只能向相邻的竖着的节点连边，竖着的只能向横着的连边．这时候如果还满流，那么就存在一种方案使得所有格子都是弯曲的：

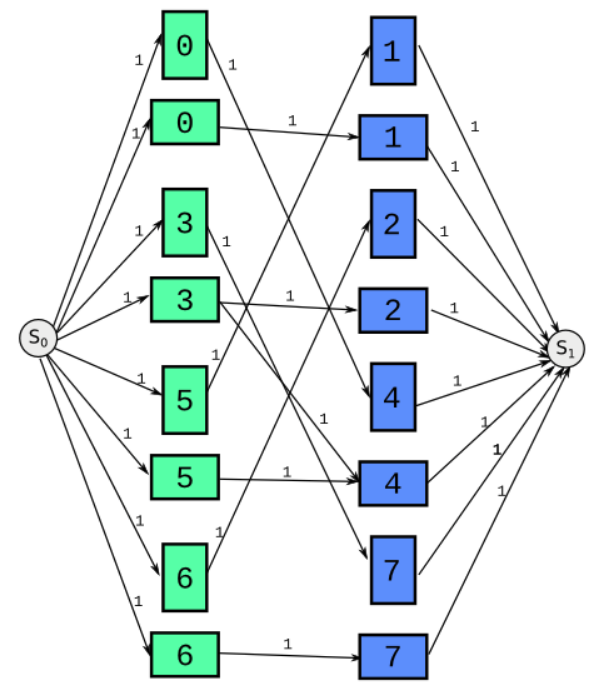
第四步，如果不满组第三步的条件，那么只需要每个节点内部横着的和竖着的连一条边，但是对于要求是弯曲形状的格子，过这条边代价就是１，否则代价就是０．然后求最小费用最大流即可．

code of problem1

#include <cmath>
#include <iostream>
#include <vector>

class RobotHerb {
 public:
  long long getdist(int T, std::vector<int> a) {
    struct node {
      int x, y, dir;
    };
    const int kDirX[] = {0, 1, 0, -1};
    const int kDirY[] = {1, 0, -1, 0};

    auto Go = [&](int dir) -> node {
      int x = 0, y = 0;
      for (size_t i = 0; i < a.size(); ++i) {
        if (kDirX[dir] != 0) {
          x += kDirX[dir] * a[i];
        } else {
          y += kDirY[dir] * a[i];
        }
        dir = (dir + a[i]) & 3;
      }
      return {x, y, dir};
    };

    auto Add = [](const node &a, long long *x, long long *y) {
      *x += a.x;
      *y += a.y;
    };

    node t[4];
    for (int i = 0; i < 4; ++i) {
      t[i] = Go(i);
    }
    long long start_x = 0, start_y = 0;
    int current_dir = 0;
    int times = 0;
    do {
      Add(t[current_dir], &start_x, &start_y);
      current_dir = t[current_dir].dir;
      ++times;
    } while (current_dir != 0);
    start_x *= T / times;
    start_y *= T / times;
    T %= times;
    for (int i = 0; i < T; ++i) {
      Add(t[current_dir], &start_x, &start_y);
      current_dir = t[current_dir].dir;
    }
    return (start_x < 0 ? -start_x : start_x) +
           (start_y < 0 ? -start_y : start_y);
  }
};

code of problem2

#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>

const int MAX = 36;

long long f[MAX][2][MAX + 1][MAX + 1];
long long g[2][MAX + 1][MAX + 1];
long long g1[2][MAX + 1][MAX + 1];

class CentaurCompany {
 public:
  double getvalue(std::vector<int> a, std::vector<int> b) {
    node_number_ = static_cast<int>(a.size() + 1);
    tree_.resize(node_number_);
    for (int i = 0; i < node_number_ - 1; ++i) {
      int u = a[i] - 1;
      int v = b[i] - 1;
      tree_[u].push_back(v);
      tree_[v].push_back(u);
    }
    Dfs(0, -1);
    long long result = 0;
    for (int n = 1; n <= node_number_; ++n) {
      for (int c = 1; c <= n; ++c) {
        if (Cost(n, c) > 0) {
          result += Cost(n, c) * Count(n, c);
        }
      }
    }
    return 2.0 * result / (1ll << node_number_);
  }

 private:
  int Cost(int n, int c) { return std::max(0, c + c - n - 2); }

  long long Count(int n, int c) { return f[0][0][n][c] + f[0][1][n][c]; }

  void Copy(long long source[2][MAX + 1][MAX + 1],
            long long sink[2][MAX + 1][MAX + 1]) {
    for (int i = 0; i <= node_number_; ++i) {
      for (int j = 0; j <= i; ++j) {
        sink[0][i][j] = source[0][i][j];
        sink[1][i][j] = source[1][i][j];
      }
    }
  }

  void Dfs(int rt, int parent) {
    for (size_t i = 0; i < tree_[rt].size(); ++i) {
      if (tree_[rt][i] != parent) {
        Dfs(tree_[rt][i], rt);
      }
    }
    memset(g, 0, sizeof(g));
    g[0][0][0] = 1;
    g[1][1][1] = 1;
    for (size_t i = 0; i < tree_[rt].size(); ++i) {
      if (tree_[rt][i] != parent) {
        int son = tree_[rt][i];
        for (int n = node_number_; n >= 0; --n) {
          for (int c = n; c >= 0; --c) {
            g1[0][n][c] = 0;
            g1[1][n][c] = 0;
            for (int n1 = n; n1 >= 0; --n1) {
              for (int c1 = c; c1 >= 0; --c1) {
                g1[0][n][c] += g[0][n1][c1] * (f[son][0][n - n1][c - c1] +
                                               f[son][1][n - n1][c - c1]);
                g1[1][n][c] +=
                    g[1][n1][c1] * (f[son][0][n - n1][c - c1] +
                                    (c1 > 0 ? f[son][1][n - n1][c - c1 + 1]
                                            : f[son][1][n - n1][c - c1]));
              }
            }
          }
        }
        Copy(g1, g);
      }
    }
    Copy(g, f[rt]);
  }

  int node_number_;
  std::vector<std::vector<int>> tree_;
};

code of problem3

#include <iostream>
#include <limits>
#include <queue>
#include <string>
#include <unordered_map>
#include <vector>

template <typename FlowType, typename CostType>
class MaxFlowMinimunCost {
  static constexpr FlowType kMaxFlow = std::numeric_limits<FlowType>::max();
  static constexpr FlowType kZeroFlow = static_cast<FlowType>(0);
  static constexpr CostType kMaxCost = std::numeric_limits<CostType>::max();
  static constexpr CostType kZeroCost = static_cast<CostType>(0);

 public:
  void Clear() {
    index_normalizer_.clear();
    node_number_ = 0;
    all_edges_.clear();
  }

  void AddEdge(int from, int to, FlowType flow, CostType cost) {
    from = GetIndex(from);
    to = GetIndex(to);
    auto idx0 = Add(from, to, flow, cost);
    auto idx1 = Add(to, from, kZeroFlow, -cost);
    all_edges_[from][idx0].sym_node_index = idx1;
    all_edges_[to][idx1].sym_node_index = idx0;
  }

  std::pair<FlowType, CostType> GetResult(int source, int sink) {
    source = GetIndex(source);
    sink = GetIndex(sink);

    struct Node {
      FlowType flow;
      CostType cost;
      int previous_node;
      int previous_edge_index;
      bool visited;
    };

    std::vector<Node> dp(node_number_);

    auto SPFA = [&]() -> FlowType {
      for (int i = 0; i < node_number_; ++i) {
        dp[i].previous_edge_index = -1;
        dp[i].flow = kZeroFlow;
        dp[i].visited = false;
        dp[i].cost = kMaxCost;
      }
      std::queue<int> bfs_queue;
      bfs_queue.push(source);
      dp[source].cost = kZeroCost;
      dp[source].flow = kMaxFlow;
      while (!bfs_queue.empty()) {
        int current_node = bfs_queue.front();
        bfs_queue.pop();

        dp[current_node].visited = false;

        for (size_t i = 0; i < all_edges_[current_node].size(); ++i) {
          int next_node = all_edges_[current_node][i].to;
          CostType cost = all_edges_[current_node][i].cost;
          FlowType flow = all_edges_[current_node][i].flow;
          if (flow > kZeroFlow &&
              dp[next_node].cost > dp[current_node].cost + cost) {
            dp[next_node].cost = dp[current_node].cost + cost;
            dp[next_node].flow = std::min(dp[current_node].flow, flow);
            dp[next_node].previous_node = current_node;
            dp[next_node].previous_edge_index = static_cast<int>(i);
            if (!dp[next_node].visited) {
              dp[next_node].visited = true;
              bfs_queue.push(next_node);
            }
          }
        }
      }
      return dp[sink].flow;
    };

    FlowType total_flow = kZeroFlow;
    CostType total_cost = kZeroCost;

    while (true) {
      FlowType flow = SPFA();
      if (IsNoFlow(flow)) {
        break;
      }
      total_flow += flow;
      for (int i = sink; i != source;) {
        int idx = dp[i].previous_edge_index;
        int pre_node = dp[i].previous_node;
        total_cost += flow * all_edges_[pre_node][idx].cost;
        all_edges_[pre_node][idx].flow -= flow;
        all_edges_[i][all_edges_[pre_node][idx].sym_node_index].flow += flow;
        i = pre_node;
      }
    }
    return {total_flow, total_cost};
  }

 private:
  bool IsNoFlow(FlowType flow) {
    constexpr double kEpsilon = 1e-3;
    return static_cast<double>(flow) < kEpsilon;
  }

  int GetIndex(int t) {
    if (index_normalizer_.find(t) != index_normalizer_.end()) {
      return index_normalizer_[t];
    }
    index_normalizer_[t] = node_number_++;
    all_edges_.push_back({});
    return node_number_ - 1;
  }

  size_t Add(int from, int to, FlowType flow, CostType cost) {
    EdgeNode node;
    node.to = to;
    node.flow = flow;
    node.cost = cost;
    all_edges_[from].push_back(node);
    return all_edges_[from].size() - 1;
  }

  struct EdgeNode {
    int to;
    FlowType flow;
    CostType cost;
    int sym_node_index;
  };

  std::vector<std::vector<EdgeNode>> all_edges_;

  std::unordered_map<int, int> index_normalizer_;
  int node_number_ = 0;
};

class CurvyonRails {
 public:
  int getmin(std::vector<std::string> field) {
    int n = static_cast<int>(field.size());
    int m = static_cast<int>(field[0].size());

    auto GetIndex = [&](int i, int j, int t) { return (i * m + j) << 1 | t; };

    auto IsGreen = [](int i, int j) { return (i & 1) == (j & 1); };

    auto IsValid = [&](int i, int j) {
      return i >= 0 && i < n && j >= 0 && j < m && field[i][j] != 'w';
    };

    MaxFlowMinimunCost<int, int> solver;
    const int source = GetIndex(n, m, 0);
    const int sink = source + 1;
    int delta_x[] = {0, 0, 1, -1};
    int delta_y[] = {1, -1, 0, 0};
    int total = 0;
    for (int i = 0; i < n; ++i) {
      for (int j = 0; j < m; ++j) {
        if (!IsValid(i, j)) {
          continue;
        }
        ++total;
        if (IsGreen(i, j)) {
          solver.AddEdge(source, GetIndex(i, j, 0), 1, 0);
          solver.AddEdge(source, GetIndex(i, j, 1), 1, 0);
          for (int d = 0; d < 4; ++d) {
            int x = i + delta_x[d];
            int y = j + delta_y[d];
            if (IsValid(x, y)) {
              int t = d >> 1;
              solver.AddEdge(GetIndex(i, j, t), GetIndex(x, y, t^1), 1, 0);
            }
          }
        } else {
          solver.AddEdge(GetIndex(i, j, 0), sink, 1, 0);
          solver.AddEdge(GetIndex(i, j, 1), sink, 1, 0);
        }
        int self_cost = field[i][j] == 'C' ? 1 : 0;
        solver.AddEdge(GetIndex(i, j, 0), GetIndex(i, j, 1), 1, self_cost);
        solver.AddEdge(GetIndex(i, j, 1), GetIndex(i, j, 0), 1, self_cost);
      }
    }
    auto result = solver.GetResult(source, sink);
    int max_flow = result.first;
    int min_cost = result.second;
    if (max_flow != total) {
      return -1;
    }
    return min_cost;
  }
};