高斯分布是一类非常重要的概率分布,在概率统计,机器学习中经常用到。
一维高斯分布
一维高斯分布的概率密度函数(pdf)形式为:

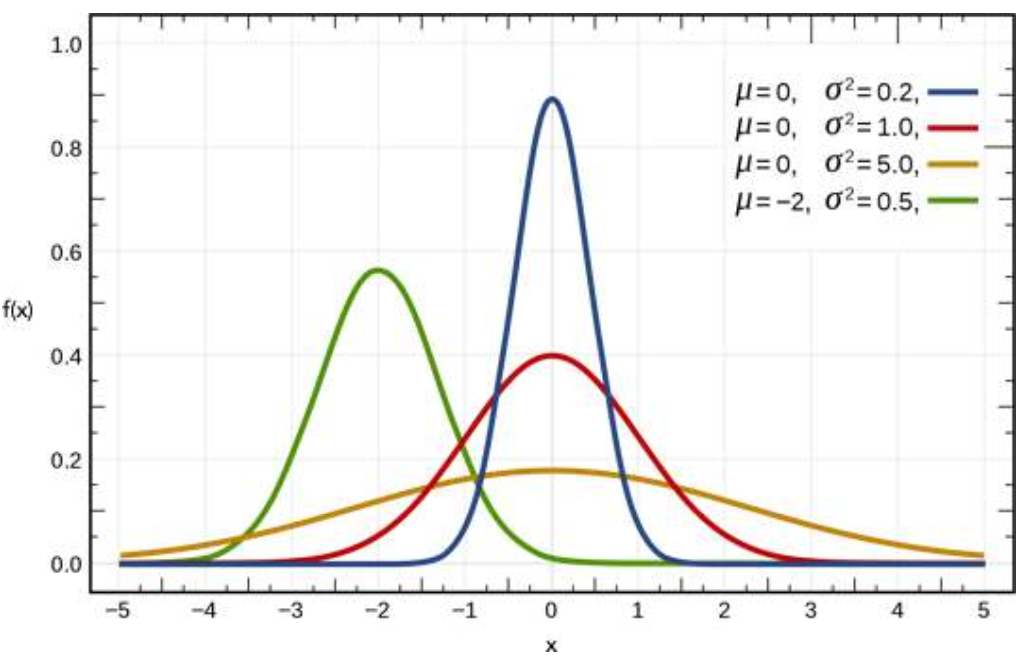
红色的曲线是标准的正态分布,即均值为0,方差为1的正态分布。
我们可以采用以下方程从均值为 μ 标准差为 σ 的高斯分布中采样(再参数化技巧):
![]()
其中,ϵ 从一个标准高斯分布中采样。
多维/多变量高斯分布
正态分布的概念可以扩展到一个以上的维度——k维的一般多元正态分布的概率密度函数如下:
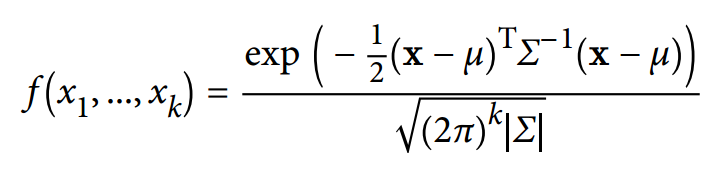
其中,|Σ|为协方差矩阵的行列式。
在2D中,均值向量μ和对称的协方差矩阵Σ定义为:
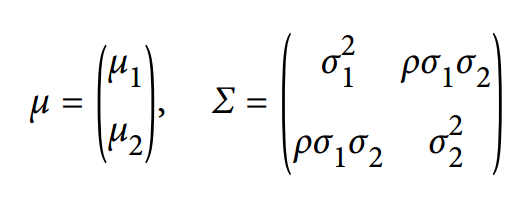
其中ρ是两个维度x1和x2之间的相关系数。

各向同性的高斯分布
各向同性的高斯分布(球形高斯分布)指的是各个方向方差都一样的多维高斯分布,协方差为正实数与identity matrix相乘。
因为高斯的circular symmetry,只需要让每个轴上的长度一样就能得到各向同性,也就是说分布密度值仅跟点到均值距离相关,而不和方向有关。
各向同性的高斯每个维度之间也是互相独立的,因此密度方程可以写成几个1维度高斯乘积形式。要注意的是,几个高斯分布乘在一起得到各向同性,但几个Laplace分布相乘就得不到各向同性!
此类高斯分布的参数个数随维度成线性增加,只有均值在增加,而方差是一个标量,因此对计算和存储量的要求不大,因此非常讨人喜欢~
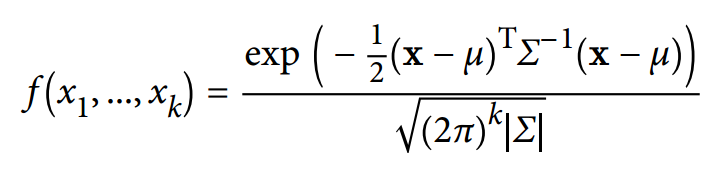
其中, Σ = σI, I为单位阵,σ为标量。

两个多元高斯分布之间的KL散度的解析表示
根据上述引理,可推导出两个多元高斯分布之间的KL散度的解析表示:
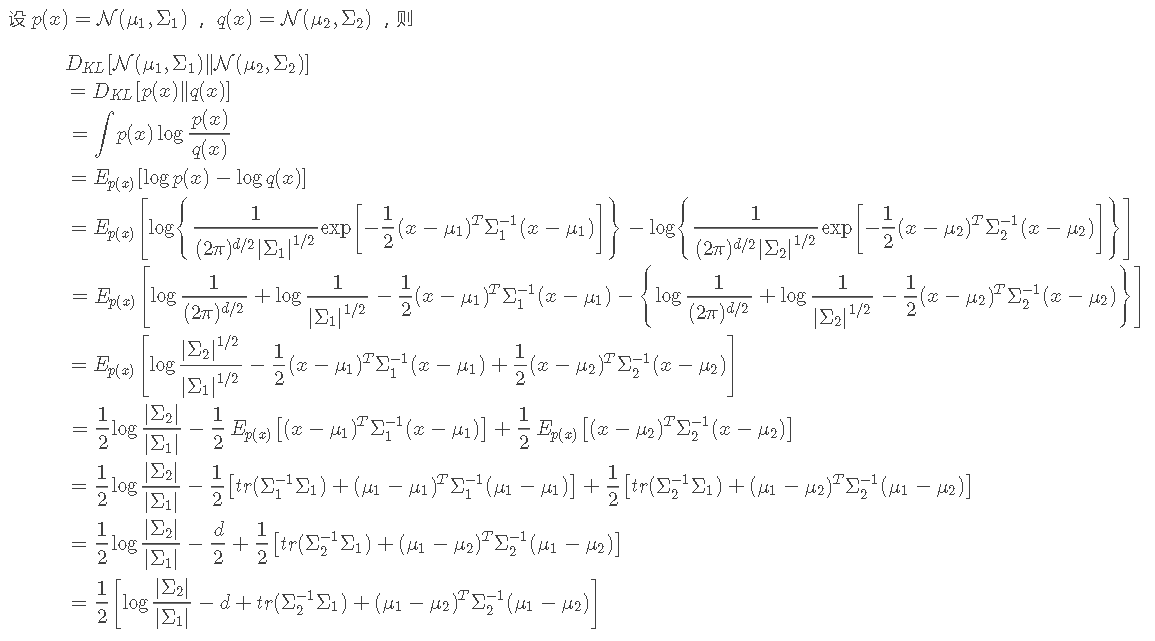
具有对角协方差矩阵的多元高斯分布与多元标准高斯分布间的KL散度
对角形式的协方差矩阵 Σ = diag(σ2), σ为标准差向量。
具有对角协方差矩阵的高斯分布每个维度之间也是互相独立的,因此密度方程也可以写成几个1维度高斯乘积形式。
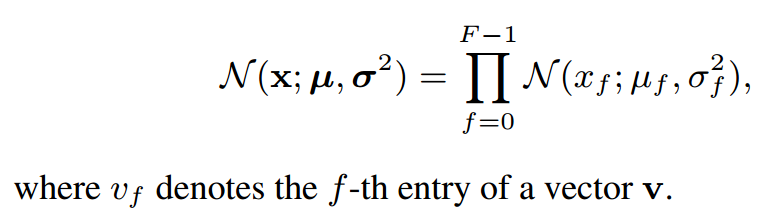


一种直观的解释方式:
注意到,密度方程可以写成几个1维度高斯乘积形式,


最后的结果是各个维度结果的加和。
复数高斯分布
随机变量是复数时,定义以下复高斯分布:

当mu=0时,该分布是圆对称的(对于x的相位偏移具有不变性)。
参考:
