排序之计数排序，基数排序和桶排序

一.计数排序

计数排序不是比较排序。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

算法的步骤如下：

1）找出待排序的数组中最大和最小的元素
2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项
3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1
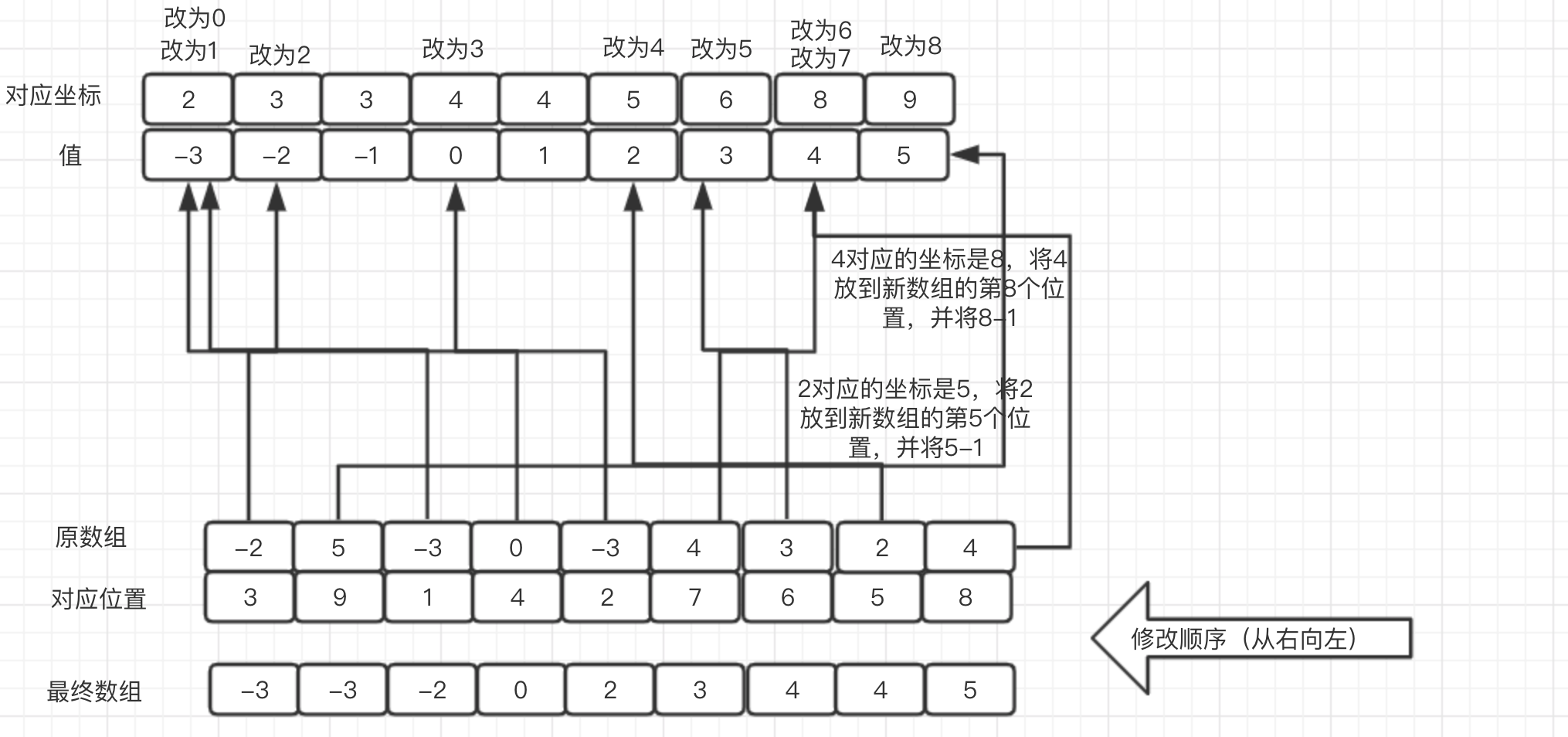
用[-2,5,-3,0,-3,4,3,2,4]这组数来模拟一下过程：

1）这组数中最大的是5，最小的是-3，所以用来计数的数组C的长度是9，

2)数组C中每个数出现的次数是2, 1, 0, 1, 0, 1, 1, 2, 1 新的数组C为[2, 1, 0, 1, 0, 1, 1, 2, 1]

3）记录每个元素的位置，其元素的最终位置都是在前一个元素的后面，所以将其中每个元素的次数更新为加上前一个元素的次数和，比如-3有两个站的位置就是2，-2有一个，位置就是2+1=3，-1没有，位置依然是3，0一个，位置是3+1=4，最终各元素的位置为：[2, 3, 3, 4, 4, 5, 6, 8, 9]

4）反向填充目标数组

 步骤如图：

def countingSort(arr):  # the elements in the array are all integers
    maximum, minimum = max(arr), min(arr)
    countArr = [0] * (maximum - minimum + 1)  #用0初始化countArr
    for i in arr: # record the number of times of every element in the array
        countArr[i - minimum] += 1
    print('--------记录每个元素出现的次数',countArr)
    for i in range(1, len(countArr)): # calculate the position of every element
        countArr[i] += countArr[i-1]  #该元素的位置是这个元素前一个元素的位置+该元素的个数
    print('---------记录每个元素的位置',countArr)
    targetArr = [None] * len(arr)  #申请一个用来放排序结果的列表
    for i in range(len(arr)-1, -1, -1): # reverse-order traversal is for the stability
        countIndex = arr[i] - minimum
        targetArr[countArr[countIndex] - 1] = arr[i]
        countArr[countIndex] -= 1
    return targetArr

a = [-2,5,-3,0,-3,4,3,2,4]


print(countingSort(a))

二.基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。基数排序的方式可以采用 LSD（Least significant digital）或 MSD（Most significant digital），LSD 的排序方式由键值的最右边开始，而 MSD 则相反，由键值的最左边开始。

算法基本步骤：

1）将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。

2）从最低位开始，依次进行一次排序。

3）从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。 

以[3,67,983,234,56,32,358,4,1]为例来模拟过程：

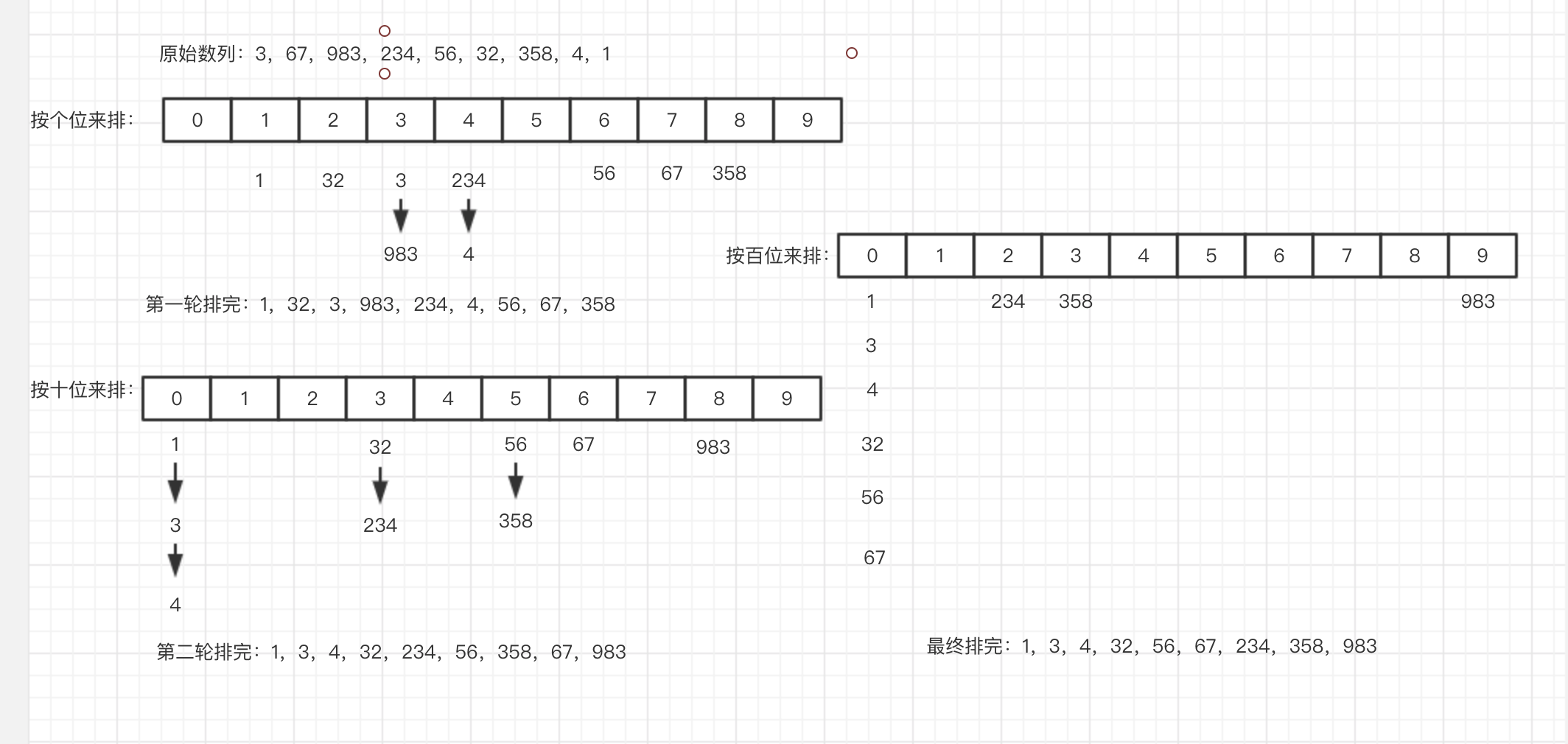
 其中的每一轮排序用的是计数排序的方法

# !/usr/bin/python
def RadixSort(input_list):
    def MaxBit(input_list):
        # 获得最大数的位数的值
        max_data = max(input_list)
        bits_num = 0
        while max_data:
            bits_num += 1
            max_data //= 10  #整除结果
        return bits_num

    def digit(num, d):
        # 取数num上的第d（从右往左第d位）位数字
        p = 1
        while d > 1:
            d -= 1
            p *= 10
        return num // p % 10

    if len(input_list) == 0:
        return []
    sorted_list = input_list
    length = len(sorted_list)
    bucket = [0] * length

    for d in range(1, MaxBit(sorted_list) + 1):
        count = [0] * 10

        for i in range(0, length):
            count[digit(sorted_list[i], d)] += 1
        # count[i]表示针对所有数的第d位数，小于等于i的数的个数是count[i]
        for i in range(1, 10):
            count[i] += count[i - 1]   #这里和基数排序很像
        # 针对所有数，按第d位数从小到大放入bucket里
        for i in range(0, length)[::-1]:
            k = digit(sorted_list[i], d)
            bucket[count[k] - 1] = sorted_list[i]
            count[k] -= 1
        for i in range(0, length):
            sorted_list[i] = bucket[i]
        print("%dth" % d)
        print(sorted_list)

    return sorted_list


if __name__ == '__main__':
    input_list = [3,67,983,234,56,32,358,4,1]
    print('input_list')
    print(input_list)
    sorted_list = RadixSort(input_list)
    print('sorted_list')
    print(sorted_list)

三.桶排序

桶排序是一种基于计数的排序算法，工作的原理是将数据分到有限数量的桶子里，然后每个桶再分别排序（有可能再使用别的排序算法或是以递回方式继续使用桶排序进行排序）。

当然桶排序更是对计数排序的改进，计数排序申请的额外空间跨度从最小元素值到最大元素值，若待排序集合中元素不是依次递增的，则必然有空间浪费情况。桶排序则是弱化了这种浪费情况，将最小值到最大值之间的每一个位置申请空间，更新为最小值到最大值之间每一个固定区域申请空间，尽量减少了元素值大小不连续情况下的空间浪费情况。

算法步骤

1）根据待排序集合中最大元素和最小元素的差值范围和映射规则，确定申请的桶个数；

2）遍历待排序集合，将每一个元素移动到对应的桶中；

3）对每一个桶中元素进行排序，并移动到已排序集合中。

以[23,45,6,7,9,12,3,10]为例来模拟过程：

def bucket_sort(array):
    maxer, miner = max(array), min(array)
    gap = (maxer - miner) // len(array) + 1
    #桶的数量
    bucket_num =  (maxer - miner) // gap + 1
    print('桶的数量',bucket_num)
    # 注意这里要+1
    bucket_size = (maxer - miner + 1) / bucket_num
    print('桶的大小',bucket_size)
    bucket = [[] for _ in range(bucket_num)]   #初始化桶
    # print(bucket)
    #将数放入桶中
    for num in array:
        bucket[int((num - miner) / bucket_size)].append(num)
    print('将数按照映射关系放到桶中',bucket)
    result = []
    #对每个桶内的数调用排序，将拍好序的数组链接起来就能得到最后结果
    for i in range(len(bucket)):
        result += sorted(bucket[i])
        print('第 %i 个桶的排序结果 '%i,sorted(bucket[i]))
    print('最终结果：',result)

arr = [23,45,6,7,9,12,3,10]

bucket_sort(arr)


##################运行结果###############

桶的数量 8
桶的大小 5.375
将数按照映射关系放到桶中 [[6, 7, 3], [9, 12, 10], [], [23], [], [], [], [45]]
第 0 个桶的排序结果  [3, 6, 7]
第 1 个桶的排序结果  [9, 10, 12]
第 2 个桶的排序结果  []
第 3 个桶的排序结果  [23]
第 4 个桶的排序结果  []
第 5 个桶的排序结果  []
第 6 个桶的排序结果  []
第 7 个桶的排序结果  [45]
最终结果： [3, 6, 7, 9, 10, 12, 23, 45]

总结：

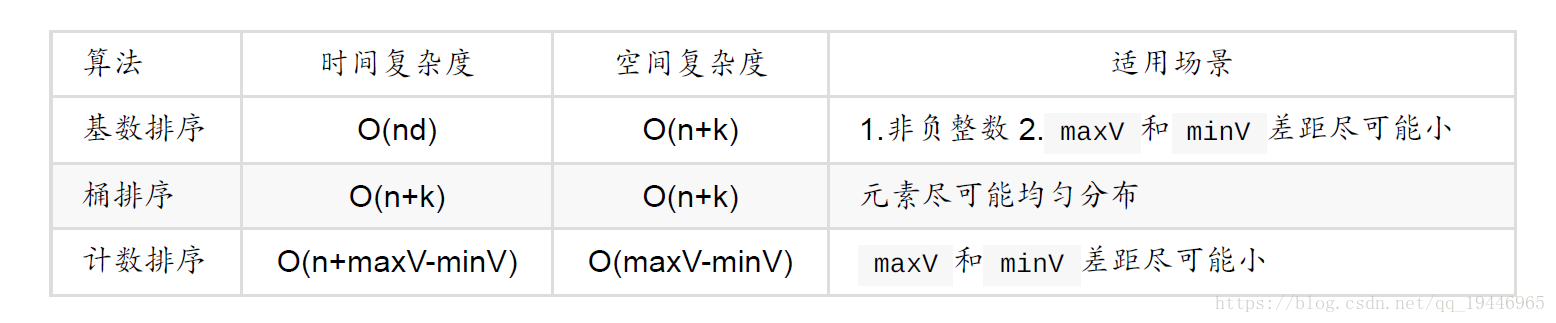
计数排序、基数排序、桶排序都属于非比较排序。非比较排序是通过确定每个元素之前，应该有多少个元素来排序。针对数组arr，计算arr[i]之前有多少个元素，则唯一确定了arr[i]在排序后数组中的位置。

计数排序需要占用大量空间，它仅适用于数据比较集中的情况。比如 [0~100]，[10000~19999] 这样的数据。

桶排序可用于最大最小值相差较大的数据情况，比如[9012,19702,39867,68957,83556,102456]。
但桶排序要求数据的分布必须均匀，否则可能导致数据都集中到一个桶中。比如[104,150,123,132,20000], 这种数据会导致前4个数都集中到同一个桶中。导致桶排序失效。

基数排序一般用于长度相同的元素组成的数组。基数排序可以看做是进行多趟桶排序。每个有效数字都在0-9之间，很适合桶排序，建10个桶很方便