树状数组

先粘上我入门时看的博客（下面部分摘自该博客）：

https://www.cnblogs.com/xenny/p/9739600.html

---

下面是我粘上以供自己复习的点：

树状数组的优点和缺点

修改和查询的复杂度都是O(logN)，而且相比线段树系数要少很多，比传统数组要快，而且容易写。

缺点是遇到复杂的区间问题还是不能解决，功能还是有限。

下面是树状数组的结构：

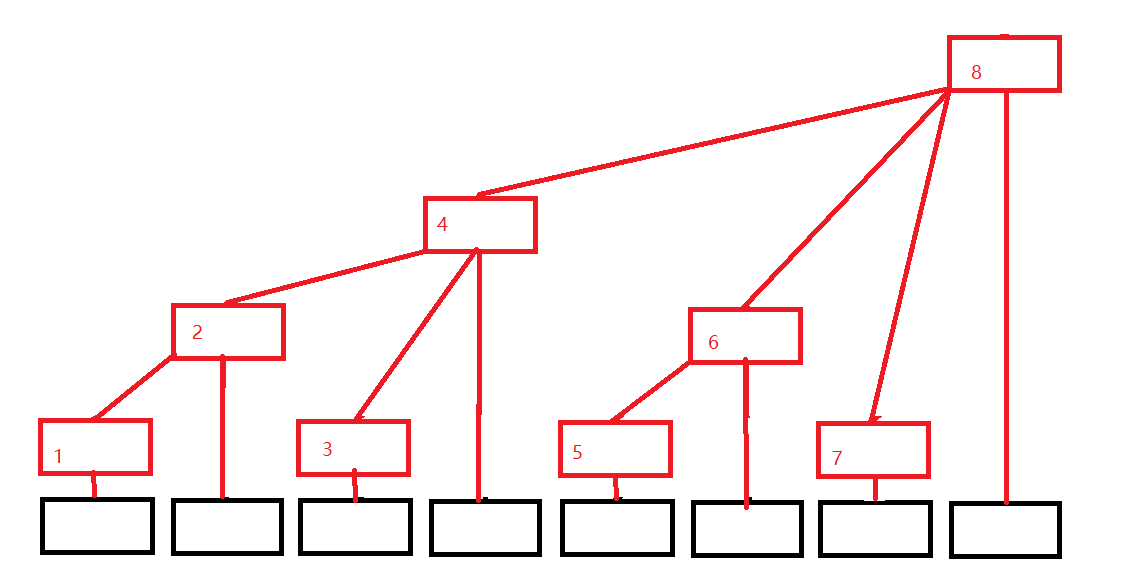
黑色数组代表原来的数组（下面用A[i]代替），红色结构代表我们的树状数组(下面用C[i]代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有

• C[1] = A[1];
• C[2] = A[1] + A[2];
• C[3] = A[3];
• C[4] = A[1] + A[2] + A[3] + A[4];
• C[5] = A[5];
• C[6] = A[5] + A[6];
• C[7] = A[7];
• C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

可以发现，这颗树是有规律的

C[i] = A[i - 2^k+1] + A[i - 2^k+2] + ... + A[i];   //k为i的二进制中从最低位到高位连续零的长度

如果我们要找前7项和，那么应该是SUM = C[7] + C[6] + C[4];

而根据上面的式子，容易的出SUM_i = C[i] + C[i-2^k1] + C[(i - 2^k1) - 2^k2] + .....；

其实树状数组就是一个二进制上面的应用。

现在新的问题来了2^k该怎么求呢，不难得出2^k = i&(i^(i-1));但这个还是不好求出呀，前辈的智慧就出来了，2^k = i&(-i);

总结一下：x&(-x)，当x为0时结果为0；x为奇数时，结果为1；x为偶数时，结果为x中2的最大次方的因子。

而且这个有一个专门的称呼，叫做lowbit，即取2^k。

如果我们更新某个A[i]的值，则会影响到所有包含有A[i]位置。如果求A[i]包含哪些位置里呢，同理有

A[i] 包含于 C[i + 2^k1]、C[(i + 2^k1) + 2^k2]...；

例题：https://vjudge.net/problem/HDU-1166

板子：

#include <bits/stdc++.h>
using namespace std;

int n,m;
int a[50005],c[50005]; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){    //在i位置加上k
    while(i <= n){
        c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求A[1 - i]的和
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    int t;
    cin>>t;
    for(int tot = 1; tot <= t; tot++){
        cout << "Case " << tot << ":" << endl;
        memset(a, 0, sizeof a);
        memset(c, 0, sizeof c);
        cin>>n;
        for(int i = 1; i <= n; i++){
            cin>>a[i];
            updata(i,a[i]);   //输入初值的时候，也相当于更新了值
        }

        string s;
        int x,y;
        while(cin>>s && s[0] != 'E'){
            cin>>x>>y;
            if(s[0] == 'Q'){    //求和操作
                int sum = getsum(y) - getsum(x-1);    //x-y区间和也就等于1-y区间和减去1-(x-1)区间和
                cout << sum << endl;
            }
            else if(s[0] == 'A'){
                updata(x,y);
            }
            else if(s[0] == 'S'){
                updata(x,-y);    //减去操作，即为加上相反数
            }
        }

    }
    return 0;
}

1.单点更新、单点查询

传统数组可做

2.单点更新、区间查询

已讲解，详细看上面

3.区间更新、单点查询

这就是第一个问题，如果题目是让你把x-y区间内的所有值全部加上k或者减去k，然后查询操作是问某个点的值，这种时候该怎么做呢。如果是像上面的树状数组来说，就必须把x-y区间内每个值都更新，这样的复杂度肯定是不行的，这个时候，就不能再用数据的值建树了，这里我们引入差分，利用差分建树。

假设我们规定A[0] = 0;

则有 A[i] = Σⁱ_{j = 1}D[j];(D[j] = A[j] - A[j-1])，即前面i项的差值和，这个有什么用呢？例如对于下面这个数组

• A[] = 1 2 3 5 6 9
• D[] = 1 1 1 2 1 3

如果我们把[2,5]区间内值加上2，则变成了

• A[] = 1 4 5 7 8 9
• D[] = 1 3 1 2 1 1

发现了没有，当某个区间[x,y]值改变了，区间内的差值是不变的，只有D[x]和D[y+1]的值发生改变，至于为什么我想我就不用解释了吧。

所以我们就可以利用这个性质对D[]数组建立树状数组，代码为：

int n,m;
int a[50005] = {0},c[50005]; //对应原数组和树状数组

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){    //在i位置加上k
    while(i <= n){
        c[i] += k;
        i += lowbit(i);
    }
}

int getsum(int i){        //求D[1 - i]的和，即A[i]值
    int res = 0;
    while(i > 0){
        res += c[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    cin>>n;27     for(int i = 1; i <= n; i++){
        cin>>a[i];
        updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
    }
    
    //[x,y]区间内加上k
    updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k
    
    //查询i位置的值
    int sum = getsum(i);

    return 0;
}

这样就把，原来要更新一个区间的值变成了只需要更新两个点。

4.区间更新、区间查询

上面我们说的差分建树状数组，得到的是某个点的值，那如果我既要区间更新，又要区间查询怎么办。这里我们还是利用差分，由上面可知

∑ⁿ_{i = 1}A[i] = ∑ⁿ_{i = 1} ∑ⁱ_{j = 1}D[j];

则A[1]+A[2]+...+A[n]

= (D[1]) + (D[1]+D[2]) + ... + (D[1]+D[2]+...+D[n]) 

= n*D[1] + (n-1)*D[2] +... +D[n]

= n * (D[1]+D[2]+...+D[n]) - (0*D[1]+1*D[2]+...+(n-1)*D[n])

所以上式可以变为∑ⁿ_{i = 1}A[i] = n*∑ⁿ_{i = 1}D[i] -  ∑ⁿ_{i = 1}( D[i]*(i-1) );

如果你理解前面的都比较轻松的话，这里也就知道要干嘛了，维护两个数状数组，sum1[i] = D[i]，sum2[i] = D[i]*(i-1);

int n,m;
int a[50005] = {0};
int sum1[50005];    //(D[1] + D[2] + ... + D[n])
int sum2[50005];    //(1*D[1] + 2*D[2] + ... + n*D[n])

int lowbit(int x){
    return x&(-x);
}

void updata(int i,int k){
    int x = i;    //因为x不变，所以得先保存i值
    while(i <= n){
        sum1[i] += k;
        sum2[i] += k * (x-1);
        i += lowbit(i);
    }
}

int getsum(int i){        //求前缀和
    int res = 0, x = i;
    while(i > 0){
        res += x * sum1[i] - sum2[i];
        i -= lowbit(i);
    }
    return res;
}

int main(){
    cin>>n;
    for(int i = 1; i <= n; i++){
        cin>>a[i];
        updata(i,a[i] - a[i-1]);   //输入初值的时候，也相当于更新了值
    }

    //[x,y]区间内加上k
    updata(x,k);    //A[x] - A[x-1]增加k
    updata(y+1,-k);        //A[y+1] - A[y]减少k

    //求[x,y]区间和
    int sum = getsum(y) - getsum(x-1);

    return 0;
}

下面是练习集（待更新）：