最小生成树（模板+入门题）

 最小生成树

加权图是一种为每条边关联一个权值(可表示成本、时间等)的图模型。这种图能表示许多场景，如航空图中边表示航线，权值表示距离或费用。在航空图中，通常的问题是如何使距离或费用最小化。

我们可以通过加权无向图的最小生成树来解决这个问题。

图的生成树：是它的一颗含有其他所有顶点的无环连通子图。一幅加权无向图的最小生成树(MST)是它的一颗权值最小的生成树(树中所有边的权值之和最小)。

我们会一起学习计算最小生成树的两种经典算法：Prime算法和Kruskal算法。

首先有几个注意点：

1. 只考虑连通图
2. 边的权值可以表示距离、时间、费用或其他变量
3. 边的权重可能是0或负数
4. 所有边的权重都不相同

我们要在一幅加权连通无向图中找到它的最小生成树。

首先定义一下  加权无向图的数据结构

最小生成树算法：Prim算法和Kruskal算法

Prim算法：

Prim算法 模板：

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <sstream>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
//const double PI=acos(-1);
#define Bug cout<<"---------------------"<<endl
const int maxn=1e4+10;
using namespace std;

struct edge_node
{
    int to;
    int val;
    int next;
}Edge[maxn*maxn/2];
int Head[maxn];
int tot;

void Add_Edge(int u,int v,int w)
{
    Edge[tot].to=v;
    Edge[tot].val=w;
    Edge[tot].next=Head[u];
    Head[u]=tot++;
}

int lowval[maxn];
int pre[maxn];//记录每个点的双亲是谁 

int Prim(int n,int st)//n为顶点的个数,st为最小生成树的开始顶点 
{
    int sum=0;
    memset(lowval,INF,sizeof(lowval));
    memset(pre,0,sizeof(pre));
    lowval[st]=-1;
    pre[st]=-1;
    for(int i=Head[st];i!=-1;i=Edge[i].next)
    {
        int v=Edge[i].to;
        int w=Edge[i].val;
        lowval[v]=w;
        pre[v]=st;
    }
    for(int i=0;i<n-1;i++)
    {
        int MIN=INF;
        int k;
        for(int i=0;i<n;i++)
        {
            if(lowval[i]!=-1&&lowval[i]<MIN)
            {
                MIN=lowval[i];
                k=i;
            }
        }
        sum+=MIN;
        lowval[k]=-1;
        for(int j=Head[k];j!=-1;j=Edge[j].next)
        {
            int v=Edge[j].to;
            int w=Edge[j].val;
            if(w<lowval[v])
            {
                lowval[v]=w;
                pre[v]=k;
            }
        }
    }
    return sum; 
}

int main()
{
    int n,m;
    scanf("%d %d",&n,&m);
    memset(Head,-1,sizeof(Head));
    for(int i=0;i<m;i++)
    {
        int u,v,w;
        scanf("%d %d %d",&u,&v,&w);
        Add_Edge(u,v,w);
        Add_Edge(v,u,w);
    }
    printf("%d
",Prim(n,0));
    return 0;
}

入门题：

Jungle Roads

http://poj.org/problem?id=1251

Description

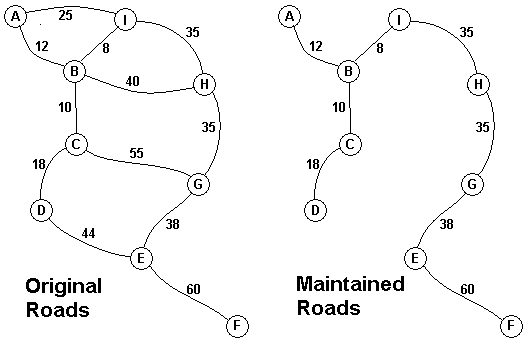
The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems. 

Input

The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above. 

Output

The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit. 

Sample Input

9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0

Sample Output

216
30

标准最小生成树，用了简化版的Prim算法，也可以用Kruskal算法

#include <stdio.h>
#include <string.h>
#include <algorithm>
#define maxn 65535
using namespace std;
int MG[1005][1005];
int F[1005];

int main()
{
    //freopen("sample.txt","r",stdin);
    int n;
    while(~scanf("%d",&n)&&n)
    {
        int sum=0,i;
        memset(MG,0,sizeof(MG));
        for(i=0;i<n-1;i++)
        {
            char c;
            scanf(" %c",&c);
            int a;
            scanf("%d",&a);
            for(int j=0;j<a;j++)
            {
                char k;
                int b;
                scanf(" %c",&k);
                scanf("%d",&b);
                MG[c-'A'][k-'A']=b;
                MG[k-'A'][c-'A']=b;
            }
            F[i]=maxn;
        }
        F[i]=maxn;
        F[0]=0;
        for(i=1;i<n;i++)
        {
            if(MG[0][i])
            {
                F[i]=MG[0][i];
            }
        }
        for(i=1;i<n;i++)
        {
            int m=maxn,t;
            for(int g=0;g<n;g++)
            {
                if(F[g]&&F[g]<m)
                {
                    t=g;
                    m=F[g];
                }
            }
            sum+=F[t];
            F[t]=0;
            for(int j=1;j<n;j++)
            {
                if(F[j]&&MG[t][j])
                {
                    F[j]=min(MG[t][j],F[j]);
                }
            }
        }
        printf("%d
",sum);
    }
    return 0;
}

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <sstream>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
//const double PI=acos(-1);
#define Bug cout<<"---------------------"<<endl
const int maxn=1e4+10;
using namespace std;

struct edge_node
{
    int to;
    int val;
    int next;
}Edge[maxn*maxn];
int Head[maxn];
int tot;

void Add_Edge(int u,int v,int w)
{
    Edge[tot].to=v;
    Edge[tot].val=w;
    Edge[tot].next=Head[u];
    Head[u]=tot++;
}

int lowval[maxn];
int pre[maxn];//记录每个点的双亲是谁 

int Prim(int n,int st)//n为顶点的个数,st为最小生成树的开始顶点 
{
    int sum=0;
    memset(lowval,INF,sizeof(lowval));
    memset(pre,0,sizeof(pre));
    lowval[st]=-1;
    pre[st]=-1;
    for(int i=Head[st];i!=-1;i=Edge[i].next)
    {
        int v=Edge[i].to;
        int w=Edge[i].val;
        lowval[v]=w;
        pre[v]=st;
    }
    for(int i=0;i<n-1;i++)
    {
        int MIN=INF;
        int k;
        for(int i=0;i<n;i++)
        {
            if(lowval[i]!=-1&&lowval[i]<MIN)
            {
                MIN=lowval[i];
                k=i;
            }
        }
        sum+=MIN;
        lowval[k]=-1;
        for(int j=Head[k];j!=-1;j=Edge[j].next)
        {
            int v=Edge[j].to;
            int w=Edge[j].val;
            if(w<lowval[v])
            {
                lowval[v]=w;
                pre[v]=k;
            }
        }
    }
    return sum; 
}

int main()
{
    int n;
    while(~scanf("%d",&n)&&n!=0)
    {
        memset(Head,-1,sizeof(Head));
        char u,v;
        int m,w;
        tot=0;
        for(int i=0;i<n-1;i++)
        {
            scanf(" %c %d",&u,&m);
            for(int j=0;j<m;j++)
            { 
                scanf(" %c %d",&v,&w);
                Add_Edge(u-'A',v-'A',w);
                Add_Edge(v-'A',u-'A',w);
            }
        }    
        printf("%d
",Prim(n,0));
    }
    return 0;
}

Networking

http://poj.org/problem?id=1287

Description

You are assigned to design network connections between certain points in a wide area. You are given a set of points in the area, and a set of possible routes for the cables that may connect pairs of points. For each possible route between two points, you are given the length of the cable that is needed to connect the points over that route. Note that there may exist many possible routes between two given points. It is assumed that the given possible routes connect (directly or indirectly) each two points in the area. 
Your task is to design the network for the area, so that there is a connection (direct or indirect) between every two points (i.e., all the points are interconnected, but not necessarily by a direct cable), and that the total length of the used cable is minimal.

Input

The input file consists of a number of data sets. Each data set defines one required network. The first line of the set contains two integers: the first defines the number P of the given points, and the second the number R of given routes between the points. The following R lines define the given routes between the points, each giving three integer numbers: the first two numbers identify the points, and the third gives the length of the route. The numbers are separated with white spaces. A data set giving only one number P=0 denotes the end of the input. The data sets are separated with an empty line. 
The maximal number of points is 50. The maximal length of a given route is 100. The number of possible routes is unlimited. The nodes are identified with integers between 1 and P (inclusive). The routes between two points i and j may be given as i j or as j i. 

Output

For each data set, print one number on a separate line that gives the total length of the cable used for the entire designed network.

Sample Input

1 0

2 3
1 2 37
2 1 17
1 2 68

3 7
1 2 19
2 3 11
3 1 7
1 3 5
2 3 89
3 1 91
1 2 32

5 7
1 2 5
2 3 7
2 4 8
4 5 11
3 5 10
1 5 6
4 2 12

0

Sample Output

0
17
16
26

有重复路径的最小生成树

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <sstream>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
//const double PI=acos(-1);
#define Bug cout<<"---------------------"<<endl
const int maxn=1e4+10;
using namespace std;

struct edge_node
{
    int to;
    int val;
    int next;
}Edge[maxn*maxn];
int Head[maxn];
int tot;

void Add_Edge(int u,int v,int w)
{
    Edge[tot].to=v;
    Edge[tot].val=w;
    Edge[tot].next=Head[u];
    Head[u]=tot++;
}

int lowval[maxn];
int pre[maxn];//记录每个点的双亲是谁

int Prim(int n,int st)//n为顶点的个数,st为最小生成树的开始顶点 
{
    int sum=0;
    memset(lowval,INF,sizeof(lowval));
    memset(pre,0,sizeof(pre));
    lowval[st]=-1;
    pre[st]=-1;
    for(int i=Head[st];i!=-1;i=Edge[i].next)
    {
        int v=Edge[i].to;
        int w=Edge[i].val;
        lowval[v]=min(lowval[v],w);
        pre[v]=st;
    }
    for(int i=0;i<n-1;i++)
    {
        int MIN=INF;
        int k;
        for(int i=0;i<=n;i++)//根据编号从0或是1开始，改i从0--n-1和1--n 
        {
            if(lowval[i]!=-1&&lowval[i]<MIN)
            {
                MIN=lowval[i];
                k=i;
            }
        }
        sum+=MIN;
        lowval[k]=-1;
        for(int j=Head[k];j!=-1;j=Edge[j].next)
        {
            int v=Edge[j].to;
            int w=Edge[j].val;
            if(w<lowval[v])
            {
                lowval[v]=w;
                pre[v]=k;
            }
        }
    }
    return sum; 
}

int main()
{
    int n;
    while(~scanf("%d",&n)&&n!=0)
    {
        memset(Head,-1,sizeof(Head));
        int m;
        scanf("%d",&m);
        tot=0;
        for(int i=0;i<m;i++)
        {
            int u,v,w;
            scanf("%d %d %d",&u,&v,&w);
            Add_Edge(u,v,w);
            Add_Edge(v,u,w);
        }
        printf("%d
",Prim(n,1));
    }
    return 0;
}

Constructing Roads

http://poj.org/problem?id=2421

Description

There are N villages, which are numbered from 1 to N, and you should build some roads such that every two villages can connect to each other. We say two village A and B are connected, if and only if there is a road between A and B, or there exists a village C such that there is a road between A and C, and C and B are connected. 

We know that there are already some roads between some villages and your job is the build some roads such that all the villages are connect and the length of all the roads built is minimum.

Input

The first line is an integer N (3 <= N <= 100), which is the number of villages. Then come N lines, the i-th of which contains N integers, and the j-th of these N integers is the distance (the distance should be an integer within [1, 1000]) between village i and village j. 

Then there is an integer Q (0 <= Q <= N * (N + 1) / 2). Then come Q lines, each line contains two integers a and b (1 <= a < b <= N), which means the road between village a and village b has been built.

Output

You should output a line contains an integer, which is the length of all the roads to be built such that all the villages are connected, and this value is minimum.

Sample Input

3
0 990 692
990 0 179
692 179 0
1
1 2

Sample Output

179

题意：

给一个初始图，再给 m条边，a,b表明a和b不需要花费时间可以直接到达，问最小生成树是多少

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <sstream>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
//const double PI=acos(-1);
#define Bug cout<<"---------------------"<<endl
const int maxn=1e4+1010;
using namespace std;

struct edge_node
{
    int to;
    int val;
    int next;
}Edge[maxn*maxn];
int Head[maxn];
int tot;
 
void Add_Edge(int u,int v,int w)
{
    Edge[tot].to=v;
    Edge[tot].val=w;
    Edge[tot].next=Head[u];
    Head[u]=tot++;
}

int lowval[maxn];
int pre[maxn];//记录每个点的双亲是谁

int Prim(int n,int st)//n为顶点的个数,st为最小生成树的开始顶点 
{
    int sum=0;
    fill(lowval+1,lowval+n+1,INF);//根据编号从0或是1开始，改+1 
    memset(pre,0,sizeof(pre));
    lowval[st]=-1;
    pre[st]=-1;
    for(int i=Head[st];i!=-1;i=Edge[i].next)
    {
        int v=Edge[i].to;
        int w=Edge[i].val;
        lowval[v]=min(lowval[v],w);
        pre[v]=st;
    }
    for(int i=0;i<n-1;i++)
    {
        int MIN=INF;
        int k;
        for(int i=1;i<=n;i++)//根据编号从0或是1开始，改i从0--n-1和1--n 
        {
            if(lowval[i]!=-1&&lowval[i]<MIN)
            {
                MIN=lowval[i];
                k=i;
            }
        }
        sum+=MIN;
        lowval[k]=-1;
        for(int j=Head[k];j!=-1;j=Edge[j].next)
        {
            int v=Edge[j].to;
            int w=Edge[j].val;
            if(w<lowval[v])
            {
                lowval[v]=w;
                pre[v]=k;
            }
        }
    }
    return sum; 
}

int main()
{
    int n;
    scanf("%d",&n);
    memset(Head,-1,sizeof(Head));
    tot=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            int w;
            scanf("%d",&w);
            if(i!=j)
            {
                Add_Edge(i,j,w);
            }
        }
    }
    int m;
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        int a,b;
        scanf("%d %d",&a,&b);
        Add_Edge(a,b,0);
        Add_Edge(b,a,0);
    }
    printf("%d
",Prim(n,1));
    return 0;
}

Truck History

http://poj.org/problem;jsessionid=72E23510BDCDD9B14969C1D265027AC0?id=1789

Description

Advanced Cargo Movement, Ltd. uses trucks of different types. Some trucks are used for vegetable delivery, other for furniture, or for bricks. The company has its own code describing each type of a truck. The code is simply a string of exactly seven lowercase letters (each letter on each position has a very special meaning but that is unimportant for this task). At the beginning of company's history, just a single truck type was used but later other types were derived from it, then from the new types another types were derived, and so on. 

Today, ACM is rich enough to pay historians to study its history. One thing historians tried to find out is so called derivation plan -- i.e. how the truck types were derived. They defined the distance of truck types as the number of positions with different letters in truck type codes. They also assumed that each truck type was derived from exactly one other truck type (except for the first truck type which was not derived from any other type). The quality of a derivation plan was then defined as 
1/Σ_(to,td)d(t_o,t_d)
where the sum goes over all pairs of types in the derivation plan such that t_o is the original type and t_d the type derived from it and d(t_o,t_d) is the distance of the types. 
Since historians failed, you are to write a program to help them. Given the codes of truck types, your program should find the highest possible quality of a derivation plan. 

Input

The input consists of several test cases. Each test case begins with a line containing the number of truck types, N, 2 <= N <= 2 000. Each of the following N lines of input contains one truck type code (a string of seven lowercase letters). You may assume that the codes uniquely describe the trucks, i.e., no two of these N lines are the same. The input is terminated with zero at the place of number of truck types.

Output

For each test case, your program should output the text "The highest possible quality is 1/Q.", where 1/Q is the quality of the best derivation plan.

Sample Input

4
aaaaaaa
baaaaaa
abaaaaa
aabaaaa
0

Sample Output

The highest possible quality is 1/3.

题意：

给出n个长度相同的字符串，一个字符串代表一个点，每两个字符串中对应位置有多少个字符不同，则不同的个数即为两点之间的距离，要求各个点都连通求quality的最大值

思路：

quality的公式已经给出，我们可以发现要让quality越大，则分母要越小，则问题转化为最小生成树问题

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
#include <math.h>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <sstream>
const int INF=0x3f3f3f3f;
typedef long long LL;
const int mod=1e9+7;
//const double PI=acos(-1);
#define Bug cout<<"---------------------"<<endl
const int maxn=1e4+1010;
using namespace std;

struct edge_node
{
    int to;
    int val;
    int next;
}Edge[maxn*maxn];
int Head[maxn];
int tot;

char str[maxn][8];

int Count(char str1[],char str2[])
{
    int ans=0;
    for(int i=0;i<7;i++)
    {
        if(str1[i]!=str2[i])
            ans++;
    }
    return ans;
}

void Add_Edge(int u,int v,int w)
{
    Edge[tot].to=v;
    Edge[tot].val=w;
    Edge[tot].next=Head[u];
    Head[u]=tot++;
}

int lowval[maxn];
int pre[maxn];//记录每个点的双亲是谁

int Prim(int n,int st)//n为顶点的个数,st为最小生成树的开始顶点 
{
    int sum=0;
    fill(lowval+1,lowval+n+1,INF);//根据编号从0或是1开始，改+1 
    memset(pre,0,sizeof(pre));
    lowval[st]=-1;
    pre[st]=-1;
    for(int i=Head[st];i!=-1;i=Edge[i].next)
    {
        int v=Edge[i].to;
        int w=Edge[i].val;
        lowval[v]=min(lowval[v],w);
        pre[v]=st;
    }
    for(int i=0;i<n-1;i++)
    {
        int MIN=INF;
        int k;
        for(int i=1;i<=n;i++)//根据编号从0或是1开始，改i从0--n-1和1--n 
        {
            if(lowval[i]!=-1&&lowval[i]<MIN)
            {
                MIN=lowval[i];
                k=i;
            }
        }
        sum+=MIN;
        lowval[k]=-1;
        for(int j=Head[k];j!=-1;j=Edge[j].next)
        {
            int v=Edge[j].to;
            int w=Edge[j].val;
            if(w<lowval[v])
            {
                lowval[v]=w;
                pre[v]=k;
            }
        }
    }
    return sum; 
}

int main()
{
    int n;
    while(~scanf("%d",&n)&&n)
    {
        memset(Head,-1,sizeof(Head));
        tot=0;
        for(int i=1;i<=n;i++)
            scanf("%s",str[i]);
        for(int i=1;i<=n;i++)
        {
            for(int j=i;j<=n;j++)
            {
                if(i!=j)
                {
                    int w=Count(str[i],str[j]);
                    Add_Edge(i,j,w);
                    Add_Edge(j,i,w);
                }
            }
        }
        printf("The highest possible quality is 1/%d.
",Prim(n,1));
    }    
    return 0;
}