有监督分类：支持向量机support vector machine（svm）

1：支持向量机

拟解决问题：如何选择一条分的开并且能够分的好的线？ 

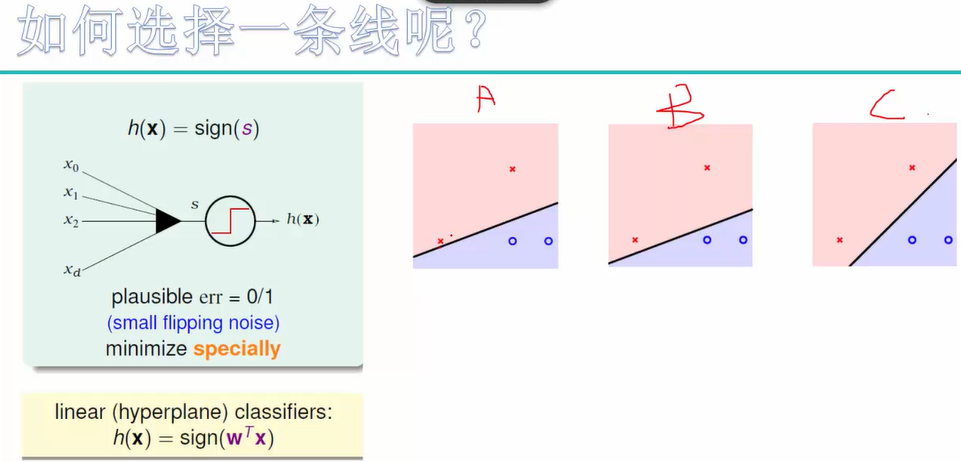
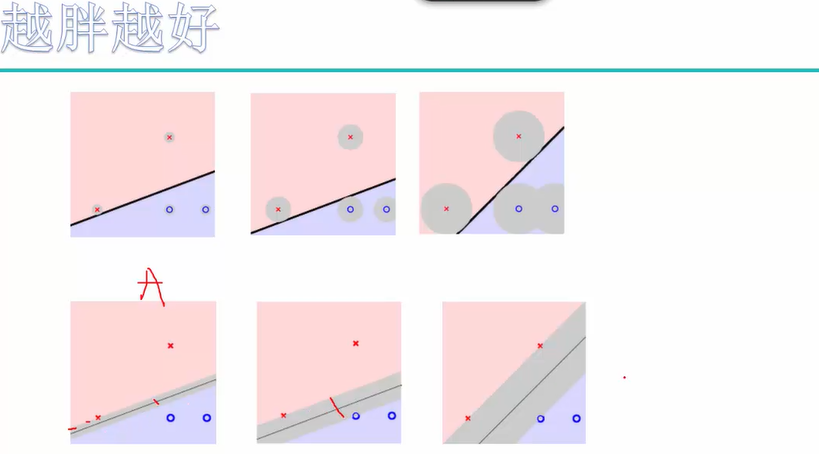
解决办法：找到一条线（w和b），使得离该线最近的点距离最远。

 公式推导：点到直线的距离？

第一步：建模，推出点到直线的一般距离公式distance(x,b,w)

 【注】w^Tx^'+b=0（即a*x+b*y+c*z+b=0）为一个平面方程，w为法向量是一个列向量,x^’为平面上的一点是一个列向量，b也为一个列向量。

第二步：代入实例，结合【第一步】的距离公式，推出样本点到直线的一般距离公式

 

第三步：根据步骤2的公式进行SVM最终目标（找到一条线，使得距离分割平面最近的点距离这条线最远）的建模。

 

 第四步：转换目标函数，以便能够使用拉格朗日乘子法求w,b，然后转换成对偶问题进行求解。

 

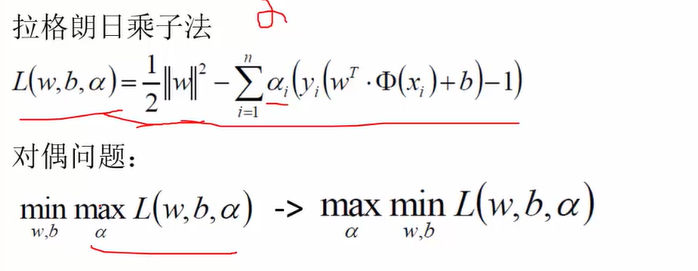
第五步：对max_amin_w,bL(w,b,a)进行求解

（1）对min_w,bL(w,b,a)求解

 

 

（2）将对a求极大值转换成求极小值

 

 (3)代入样本点，求解最小值对应的a(阿法)值

 

 

 

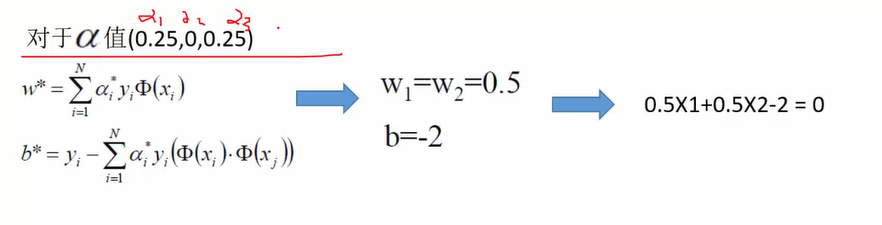
 故w和b的求出，便可以知道选择哪一条线既可以分的分的开又可以分的好了。

a(阿法)的求出，便可以知道哪些样本点为支持向量了。

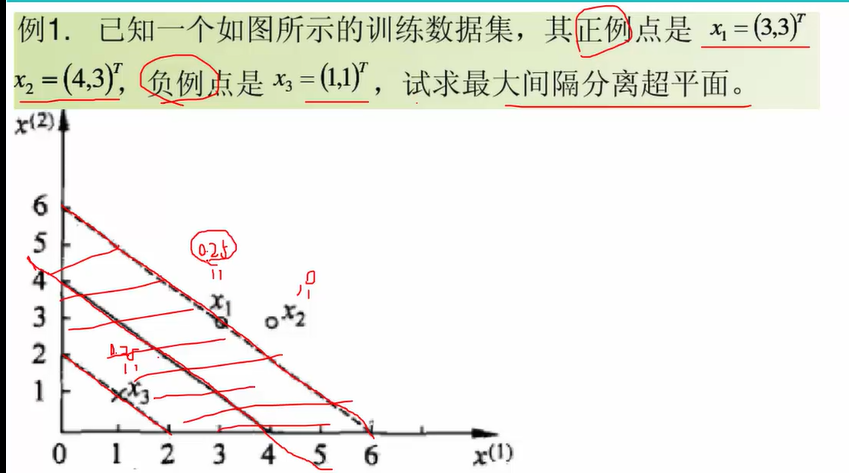
（4）由于a(阿法)₂=0，故x₂未参与计算，故x₁和x₃为计算最大间隔分离超平面的支持向量。

 

 2：软间隔支持向量机

拟解决问题：离群点的出现，可能会导致支持向量机过拟合。

 解决办法：引入松弛因子，加大了对a(阿法)的限制，增大了支持向量机的泛化能力。