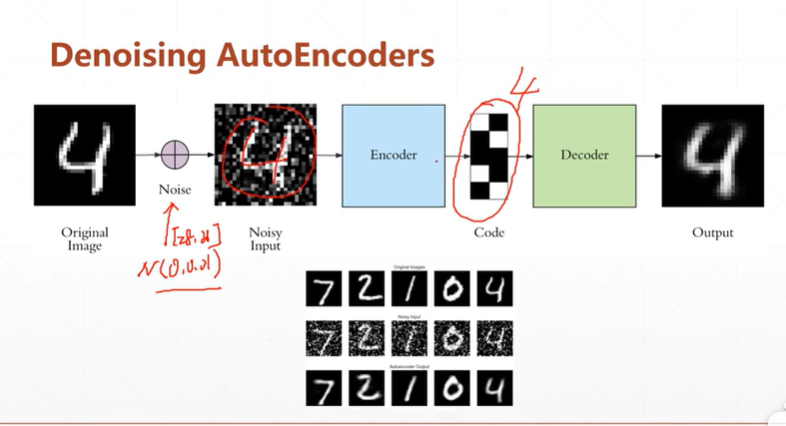
1：Denoising AutoEncoders去噪自编码网络
2.Dropout AutoEncoders断掉部分网络连接的自编码网络
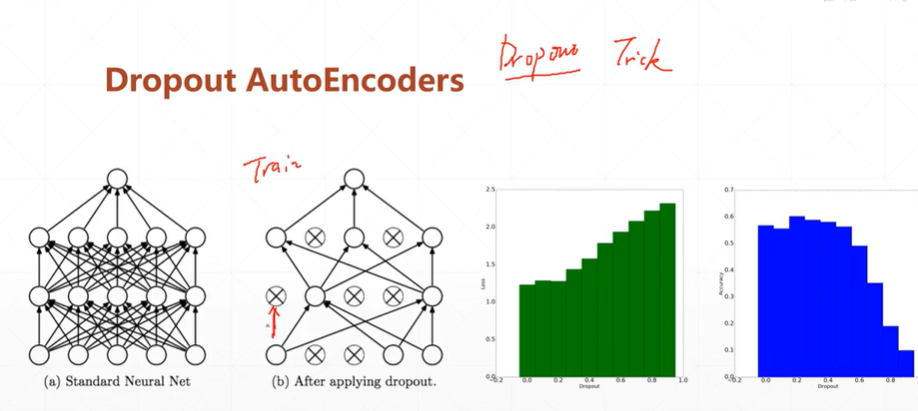
【注】从右边的直方图分别为loss,acc随着dropout变化而变化的直方图。可以看出，当dropout=0时，loss最小可能会导致过拟合现象的发生，所以在acc中可以看出当dropout=0时并不是最高。当适当提高dropout=0.2可以发现其loss较低，acc效果更好。故适当的dropout可以提高训练效果
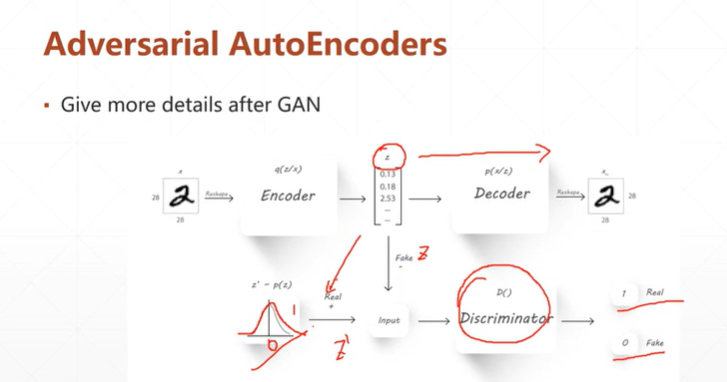
3：Adversarial AutoEncoders 对抗自编码器AAE
4：variance autoencoders 变分自动编码器VAE（当看完4.1-4.4不能看懂，可以直接看4.6，相信你通过一个例子就明白了）
（4.1）该种自编码网络的公式
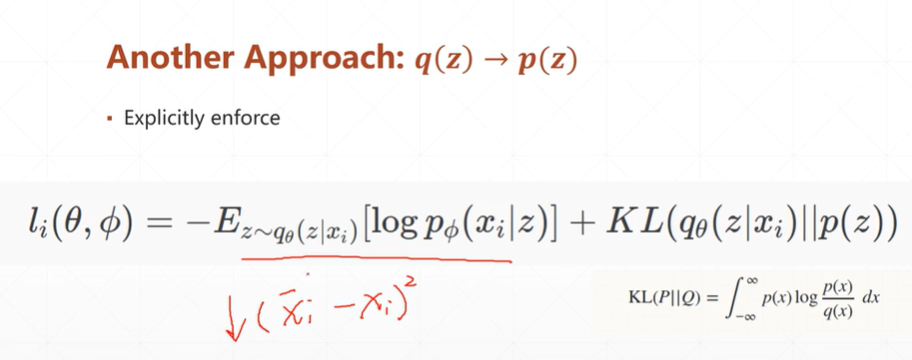
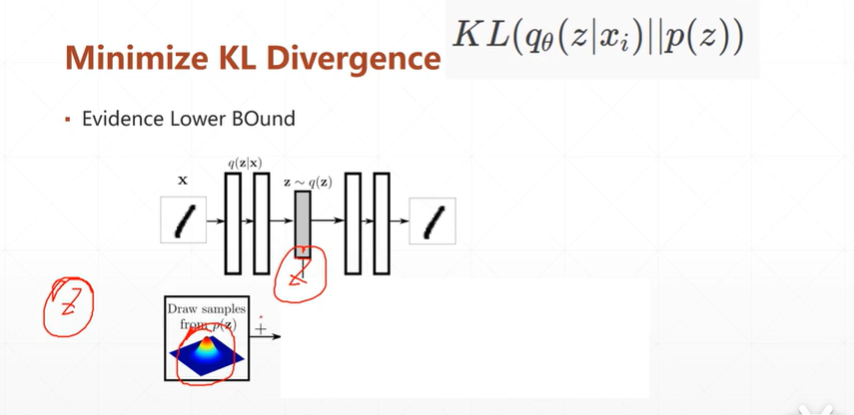
[注]这种方法与3类似，是通过KL散度来将分布逼近到某一个分布。
[注]公式的第一部分是数据通过两个网络重构自己的损失。第二部分是KL散度，目的是为了将数据分布（Q也即是：q_Θ(z|x_i)分布）逼近到一个指定的分布（P也即是：p(z)分布）。
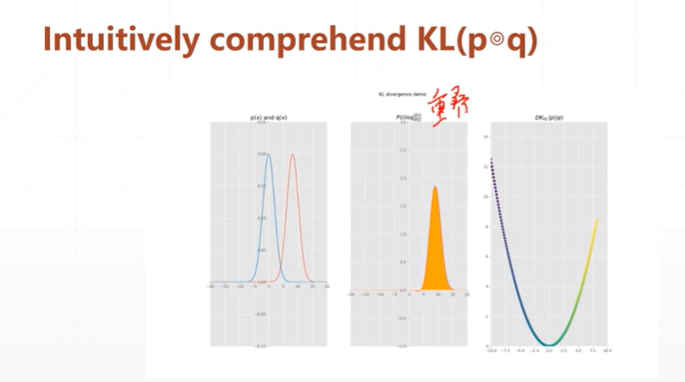
[注]从上图可以看出，当数据分布重叠时，KL的值最小。
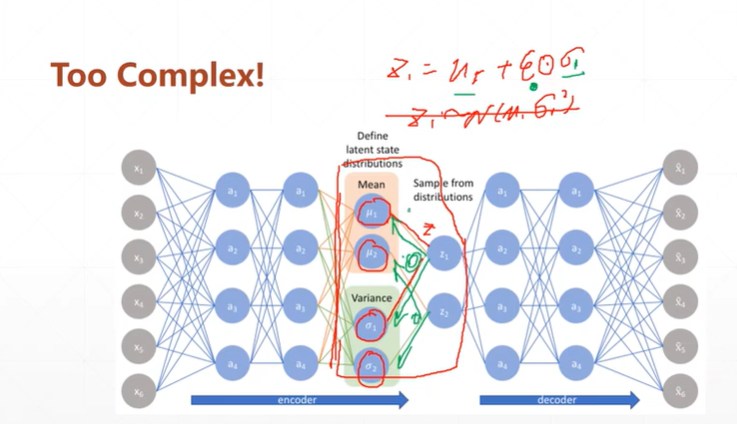
（4.2）由于Z无法对正太分布求导，该如何解决？
【注】由于该种网络，是由x通过encoder模型->正太分布N().sample->通过decoder模型得到x'.当返回优化时，sample抽样操作无法进行微分。而别的自编码网络则是x->h->x'。h为降维或升维后的数据，故反向时候可以微分。
解决办法（该方法发表在2014年的一篇文章中）：
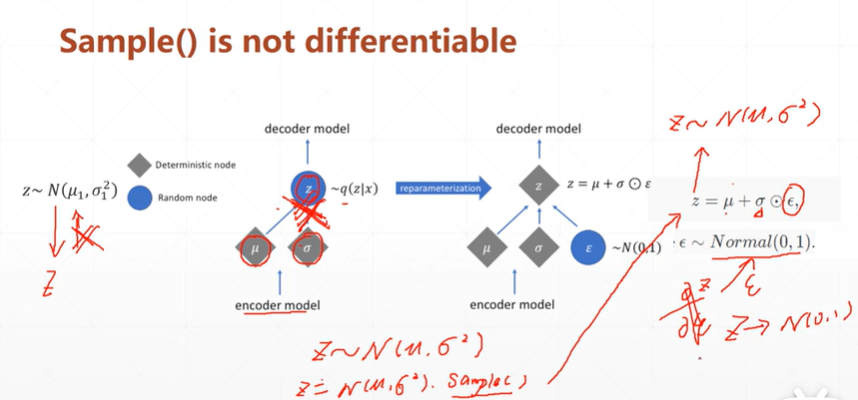
【注】可以通过将其抽样过程转换为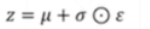
，此时的Z依旧是符合N(μ,ó*ó)。再次方向优化时就可以进行微分了，虽然ξ也不可以微分，但此时已经不需要对它进行优化了，而是一个标准的正太分布N(0,1)。
（4.3）到底要不要加KL？可以添加参数β进行调节。
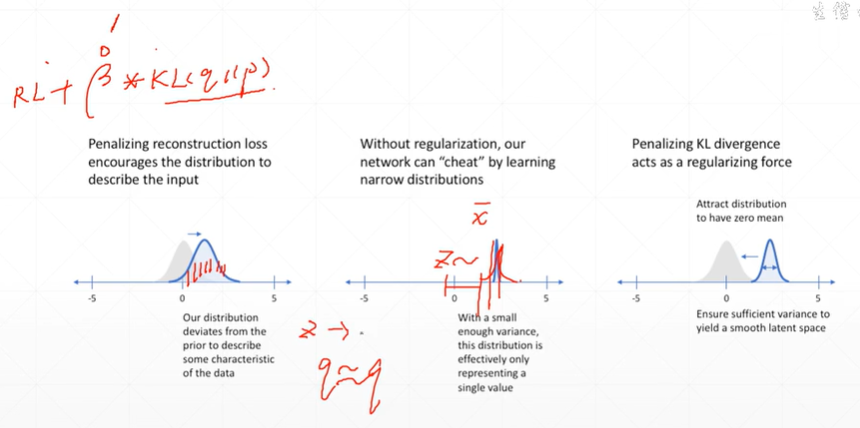
（4.4）对于VAE理解太复杂怎么办？可以这样理解
（4.5）AE与VAE的效果对比；VAE VSGAN
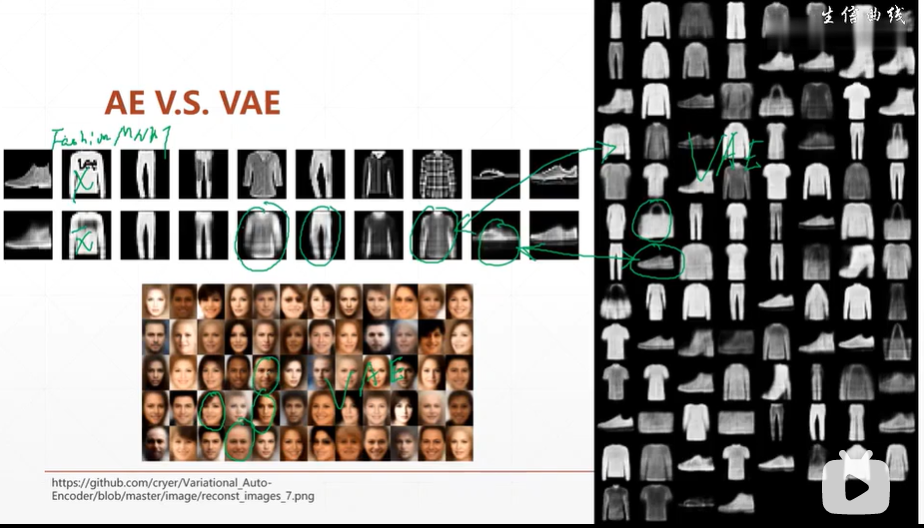
【注】由于VAEencoders生成数据特征的分布，故不同的抽样可以同GAN一样生成很多图片。
(4.6)VAE的举例帮助更好的理解：
