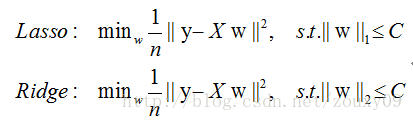机器学习算法笔记
云计算大数据和人工智能





机器学习算法简介

决策树算法





刚才我们使用的就是ID3算法
分类回归树

半监督学习

集成学习

多种或者多个学习器解决同一个问题
Bagging


Boosting

对上一次预测错误的样本的权重加大

随机森林


深度学习简述

增强学习简述

迁移学习简述

机器学习方法三要素




期望风险往往无法计算
在样本较小时,如果只关注经验风险,很容易过拟合
加上正则项之后,防止过拟合:

例如:
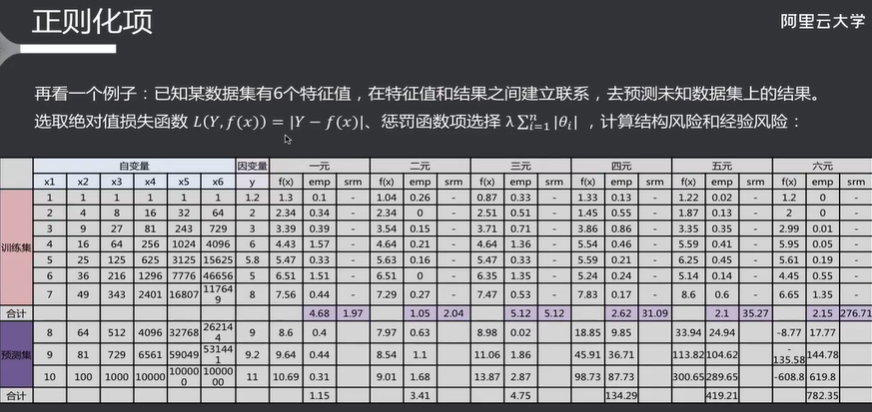
惩罚函数项表示参数个数


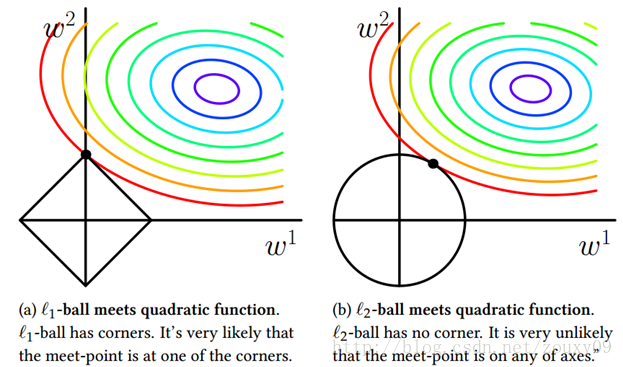
常用L1和L2范数,左图为L2,右图为L1
L1回归为lasso回归,L2为ridge回归
对于上图的理解:
实际上,对于L1和L2规则化的代价函数来说,我们可以写成以下形式:
cost function的形式就为:
通过加入此惩罚项进行优化后,限制了回归系数wiwi的绝对值,数学上可以证明上式的等价形式如下:
也就是说,我们将模型空间限制在w的一个L1-ball 中。为了便于可视化,我们考虑两维的情况,在(w1, w2)平面上可以画出目标函数的等高线,而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解:
模型的评估与选择
评估方法
基础是交叉验证

留1法要对每一条数据都单独拿出来一次做测试



上面说的有问题,应该是有放回的抽样
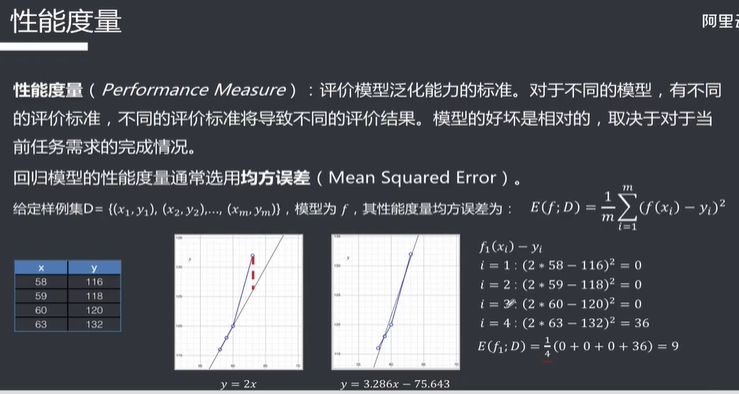
性能度量

比较检验


这个完全就是概率统计里的知识
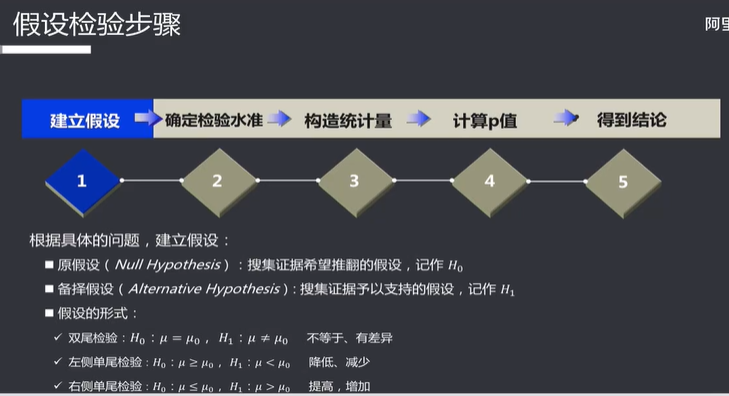
拿个例子复习下:

偏差与方差

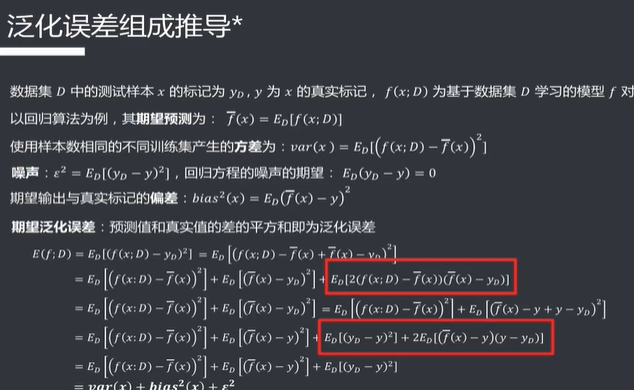
期望泛化误差=方差(模型稳定性)+偏差(模型准确性)+噪声(数据准确性)
回归分析
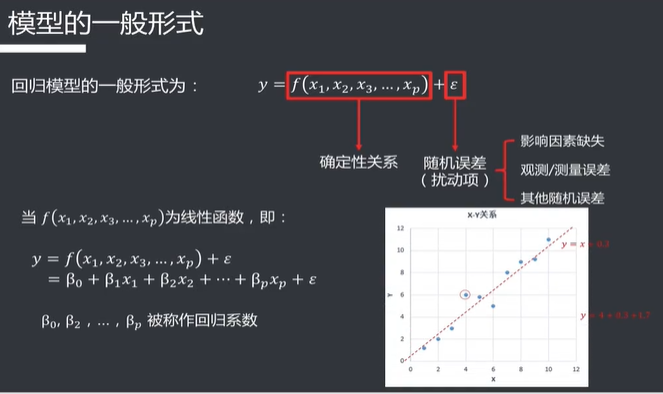

最小二乘估计
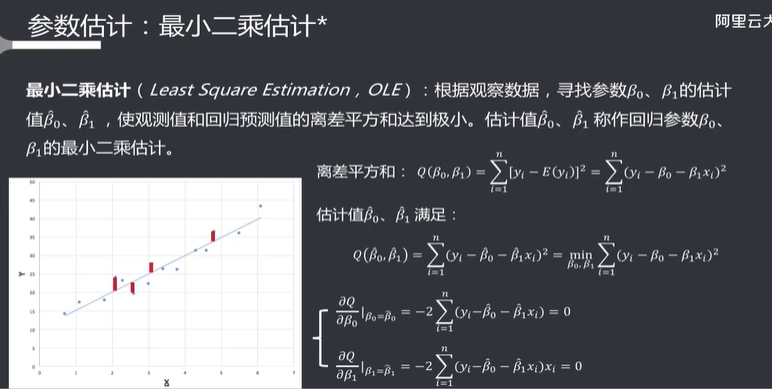
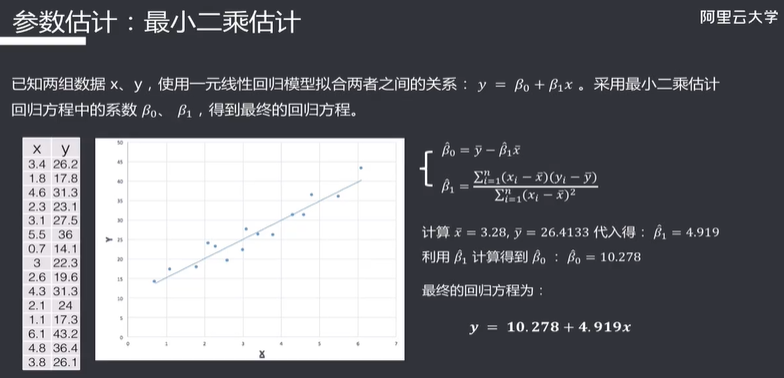
另外一种方法是最大似然估计,它适用于解决参数未知的情况
最大似然估计


有偏估计和无偏估计

最后一个式子的推导如下:
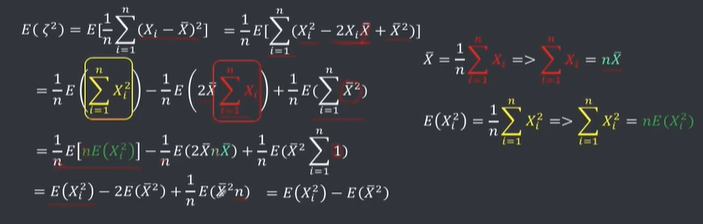
而
所以S^2才是样本方差的无偏估计
相关系数
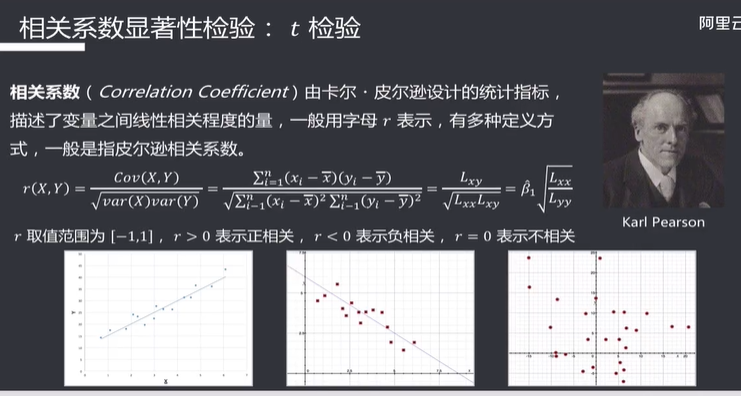
显著性检验
还使用OLE的例子:

t检验:回归系数检验

对于单元和多元线性回归,回归系数检验都是一样的,都是一次只检验一个变量:

F检验:回归方程检验
yihat是yi的估计值,y杠是yi的平均值
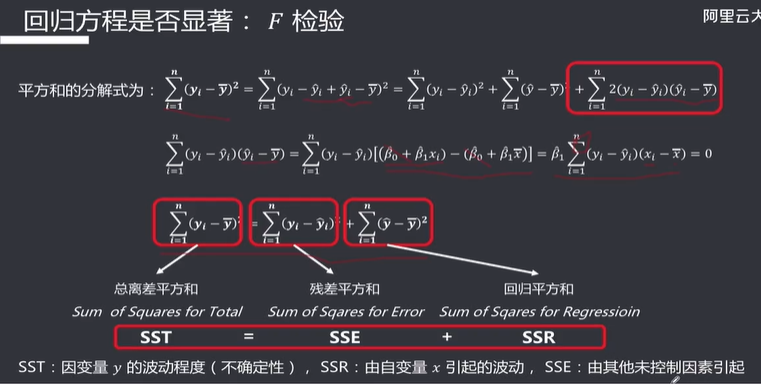
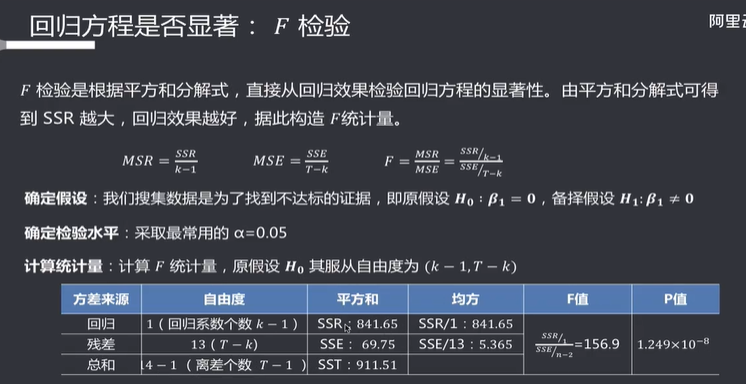
k是回归系数个数,T是样本的个体数
可以看到,对于一元线性回归,F检验和t检验的假设是一样的。但是在多元线性回归中则不一样。回归方程显著性检验,检验的是自变量和因变量总体是否有联系,而不是只看某一个自变量:


决定系数

相关系数显著性检验


相关系数显著性检验是来检验计算得到的相关系数是否符合总体相关系数
残差分析

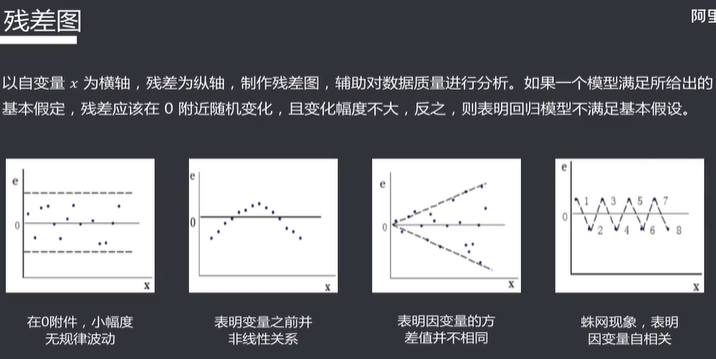

模型应用




综合案例:

多元线性回归



lnL最小,等价于y和Xβ最接近,等价于离差平方和最小
自变量的标准化


相关系数

这个在单元线性回归中是没有的,因为单元只有一个自变量

回归模型诊断与优化
违背基本假设

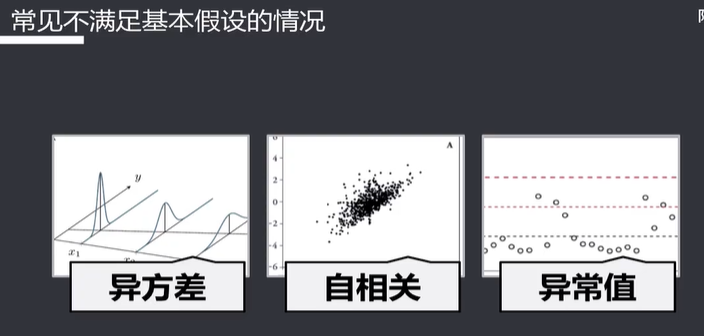
异方差



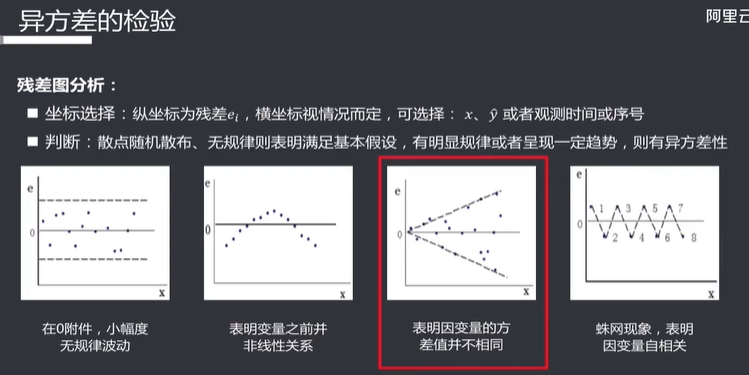


实例:
异方差的意义是很重大的,它可以用来评估我们的模型是不是过分简单了、是不是需要提高维度
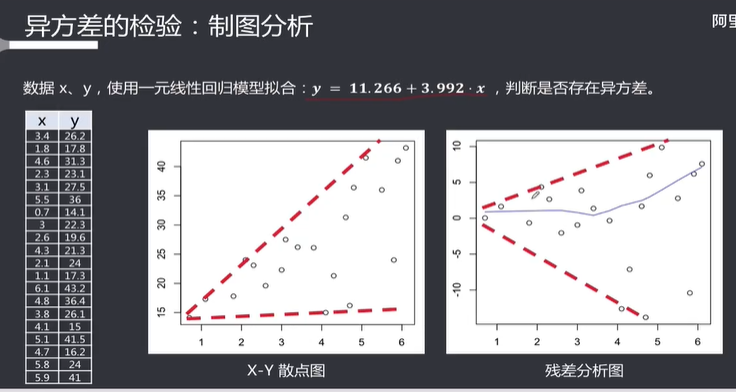
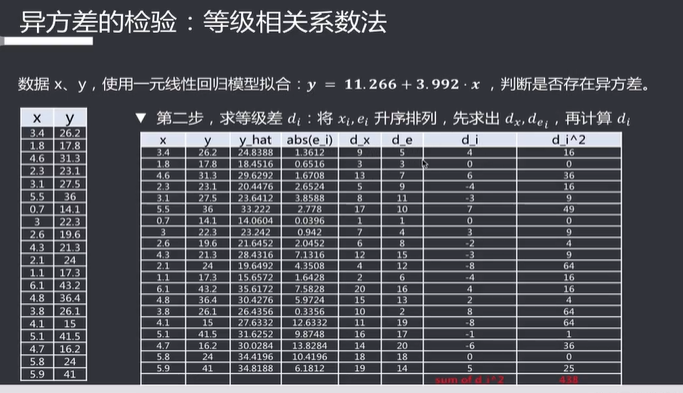

异方差导致使用最小二乘法计算得出的不是最小方差的线性无偏估计



可以看到还原回去之后已经不是一个一元线性方程了,说明我们直接用一元线性方程来建模是不合适的
自相关



一阶:后一个值只和前一个值有关

迭代法

ut是满足0均值,同方差、不相关的

差分法

BOX-COX变换

λ是可求的,但是在实际操作中我们一般不去求解析解,而是直接给出一些取值,然后选取效果最好的一个




λ是试出来的,不太好确定
异常值


自变量选择


SSE:残差平方和


具体操作上:




后退法的计算量比前进法大
如果所有自变量都是独立的,理论上前进法和后退法得到的回归方程是一致的

多重共线性





多重共线性是导致选模型预测误差和残差方差较小的原因之一
例如:


改进的回归方法
岭回归



例如:

LASSO回归


Logistic回归
模型原理




参数估计








模型评估、诊断与调优
回归方程假设检验:

回归系数假设检验:

拟合优度:

logistics模型还可以用分类模型的指标来评价:

自变量筛选:


SVM





拉格朗日乘子法






要对C的取值分类讨论:




推导:


也就是将min(x)和max(λ,μ)互换位置

求解超平面





核函数和松弛变量








朴素贝叶斯






似然函数是通过要求某一结果出现的概率最大而求解参数值的方法:即如果结果真是发生,就要求其发生的概率是最大化的


所以最大后验估计经常被诟病主观性太强了


最大似然估计其实是最大后验估计的一种特殊情况:当认为先验概率是均匀分布的话,也就是对任何值先验概率都是固定的话,最大后验估计就简化为了最大似然估计

朴素贝叶斯假设属性之间相互独立,如果属性实际上不符合这个要求的话,误差是比较大的



神经网络概述





RNN:循环神经网络
上面的RNN可以展开为:


学习规则
赫布学习规则

赫布学习规则是无监督的学习方式
把每个样本代入进去:

离散感知器学习规则
离散感知器学习规则是有监督的学习方法

连续感知器学习规则

损失函数



最小均方学习规则


相关学习规则

相关学习规则只考虑期望输出
竞争学习

例如:

外星学习规则

感知机

多层感知机



两个隐藏层就可以生成任意复杂形状的判决域
自适应线性单元

因为使用了线性的激活函数,所以输出值是连续的,而不是离散的
量化函数:将连续的输出离散化以用于分类,回归的话不需要加


BP算法

BP的推导见这里:https://www.cnblogs.com/jiading/p/11706891.html




BP算法的改进



竞争神经网络



自组织神经网络是前馈无监督网络,通常使用竞争学习的方法

自组织特征映射神经网络(SOM)
SOM是无监督算法


对周围神经元同时有促进和抑制的效果




实例:



找到最大的值,对其和其邻域进行更新:




注意在这里我们是在10x10的每个格子中都选择值最大的所对应的那个类,这就会出现有些类在结果中无法体现出来,因为它的值可以在哪个格子上对应的都不是最大的:

例如本例中的eagle
学习向量量化神经网络(LVQ)

LVQ是竞争学习和有监督学习的结合




对偶传播神经网络(CPN)

划重点,存储二进制或者模拟值的模式对


注意调整输入层到竞争层时“对比”的不是label而是输入

上图标题写错了,应该是输出层
可以看到,CPN对于输入层到竞争层的权重和竞争层到输出层的权重是分阶段调整的,不是一次同时进行调整
改进:双获胜神经元

记忆能力、容量等会更强一些
左侧展示的就是CPN的联想记忆功能
可以看到,右侧的联想其实是把左侧的两个联想的情况组合了起来,组合的输入对应的组合的输出
自适应共振理论网络(ART)

注意这里讲述了遗忘的概念

R层会输入C层,C层的输出又会传到R层

G2对R层整体起作用

对于C层的每个节点,其都有三个输入,输出值是采用投票的方式决定的。在一开始G1为1,此时如果x1为1,则1占多数,输出是1;如果x1是0,则0占多数(因为此时t1是0);当t1不再一直为0时,G1变成0,此时就变成了只有t1和x1同时为1时输出才是1,否则就是0.

门限值就是设定的测量标准





具体算法:

注意ART每个输入的分量都是二进制的


反馈神经网络
什么是反馈神经网络:



Hopfield网络

DHNN(离散Hopfield网络)





这里的思路很妙:因为能量总是有趋于最小化的趋势的,而我们可以用式子将能量代数的表示出来,所以我们如果使用能量的代数式,就可以保证其能在变化中自动趋于全局最小点
能量函数不是直接用的,而是它定义了更新状态的方式,我们更新时要符合能量函数的式子


如果对角线元素值不是0的话,第三个简化的图中每个节点还应该有一个自环

每个xi都是一个标量
注意我们是不更新系数和阈值的,只更新输入。相当于一种网络最后对应一个稳定状态的X
注意上面有一个“假稳定”,实际上还没有到达稳定


注意这一点:更新的先后顺序会影响状态的变化


这里要注意的是,虽然可能只有1/3的概率可以直接进入下一个状态,但是只要我们遍历一次节点,就一定能进入下一状态,直到收敛到最终状态:



由上图可知,无论选择哪一个初始状态都会最终收敛到最终状态的:

只有011是稳定状态,所以无论怎样变化,最终一定收敛到011


- 保证权值矩阵是对称的
- 如果平衡点是011,那要保证输入011至少应该能达到011平衡点

就是说如果输入就是吸引子的话,要保证状态不会转移出去。当然这并不能完全保证对其他的状态能否收敛到该状态

通过解不等式的方法可能求出多组解
解出来之后要验证其是否是吸引子(因为我们求解只是满足了一个必要条件):

另外一个办法就是外积法

减去一个单位矩阵是为了让对角线为0
例如:

伪稳定点指的是虽然是稳定点,但不是我们最初设计的吸引子之一,这不是我们想要的结果
注意有些状态在并行下会陷入极限环,不能收敛:

案例:OCR字符识别

效果一般,因为状态之间的重叠太大了,我们可以将输入更加精确化:

CHNN(连续Hopfield网络)
DHNN支持同步和异步,而CHNN主要是同步



了解,了解即可


TSP旅行商问题

输出是什么:




双向联想记忆神经网络(BAM)

重点是双向联想
只有两层。因为是双向的所以也无所谓输入和输出之分

稳定之后网络就训练完成了


随机神经网络


模拟退火算法

P表示取新值的概率


自联想和异联想



其他常见神经网络
径向基函数神经网络(RBF NN)


深度神经网络(DNN)

递归神经网络(RNN)

长短期记忆网络(LSTM)

深度信念网络(DBN)

生成对抗网络(GAN)