机器学习-正则化+回归与分类辨析
这篇文章是对自己早期一篇讲正则化和回归的补充。当时写作那篇文章的时候自己还刚刚入门机器学习，许多知识是理解了，但是缺少从一定的高度上的总结。结合这篇来看原来的那篇，不容易乱。
首先要明确，正则化不是回归的专利，回归和分类都是可以使用的。在回归中使用正则化就是岭回归（L2正则化）和Lasso（L1正则化），在分类中使用就是我们常见的loss function中的正则项了（其实还有一个方面的应用，知乎这位答主提到了，就是直接构造loss function,例如L1正则就构造成这样：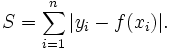
，L2正则就构造成这样:
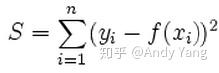),在例如sklearn中的模型中都有对应的参数选择。
至于L1和L2正则的取舍，可以看上面我提到的知乎回答的其他一些答案:
L0范数：向量中非0元素的个数。
L1范数(Lasso Regularization)：向量中各个元素绝对值的和。
L2范数(Ridge Regression)：向量中各元素平方和求平方根。
L0范数和L1范数都能够达到使参数稀疏的目的，但L0范数更难优化求解，L1范数是L0的最优凸相似且更易求解，故得到广泛的应用。
L2范数主要作用是防止模型过拟合，提高模型的泛化能力。
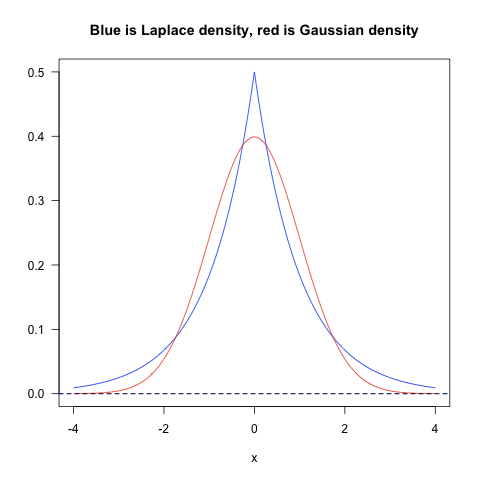
L1是蓝色的线，L2是红色的线，很明显，L1的分布对极端值更能容忍。那么如果数据损失项使用L1 Norm，很明显，L1 Norm对outlier没有L2 Norm那么敏感；如果正则化损失项使用L1的话，那么使学习到的参数倾向于稀疏，使用L2 Norm则没有这种倾向。
实践中，根据Quaro的data scientist 的经验，实际应用过程中，L1 nrom几乎没有比L2 norm表现好的时候，优先使用L2 norm是比较好的选择。
其实从某一方面来说，分类和回归的区别就体现了阈值的有无上，设置了阈值判断的回归就是分类。其实仔细想想，分类和回归问题在机器学习和深度学习上差不多是半斤八两，只是因为自己现在做的是计算机视觉的目标检测，所以对分类模型比较重视，在其他的领域，例如预测股票等等之类的场景，回归问题还是很多的，两者的区别就体现了网络结构的设计上，但是如果都是有监督学习的范畴内的话，区别真的不太大，例如这个知乎问题所说。