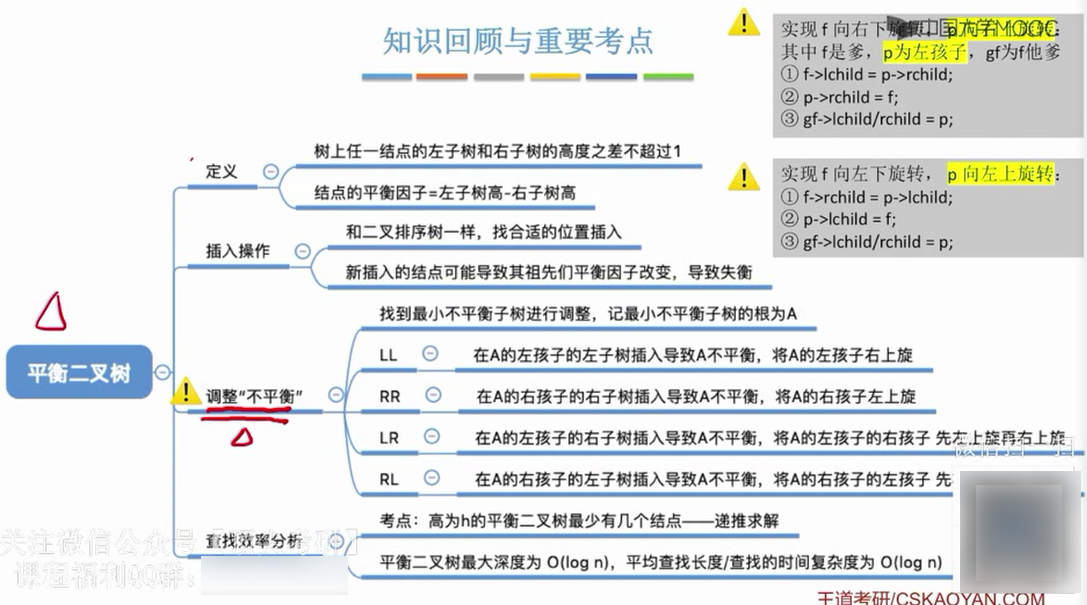
平衡二叉树（AVL）

平衡二叉树（AVL）

平衡二叉树的定义：树上任何一个结点的左子树和右子树的高度差不超过1.

结点的平衡因子：左子树高-右子树高

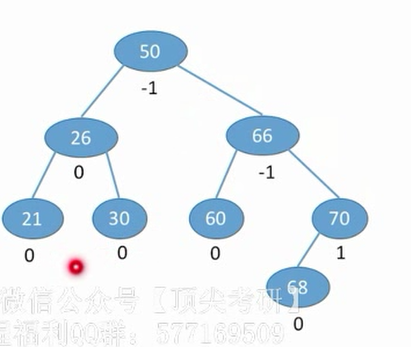
平衡二叉树的结点的平衡因子值只可能是1，-1，0.

//平衡二叉树结点
typedef struct AVLNode{
    int key;				//数据域
    int balance;			//平衡因子
    struct AVLNode *lchild,*rchild;
}AVLNode,*AVLTree;

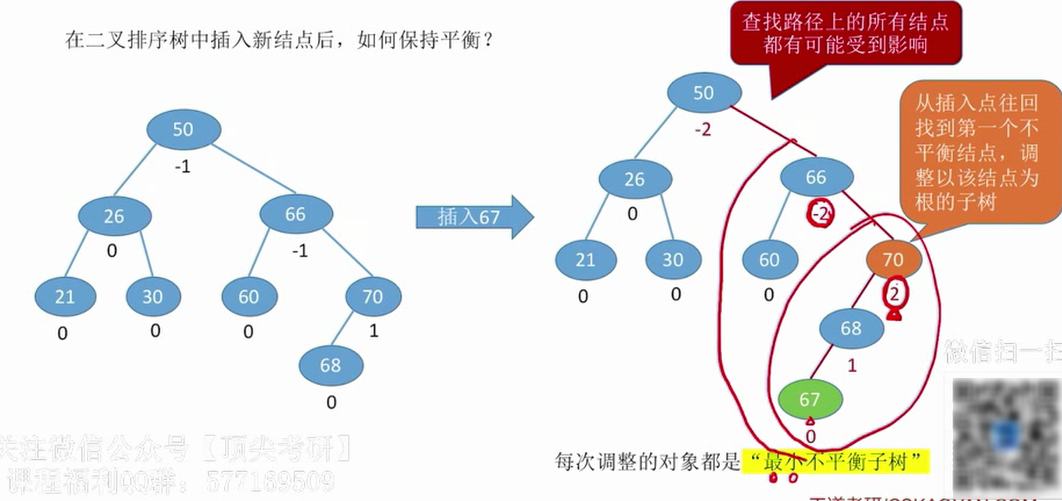
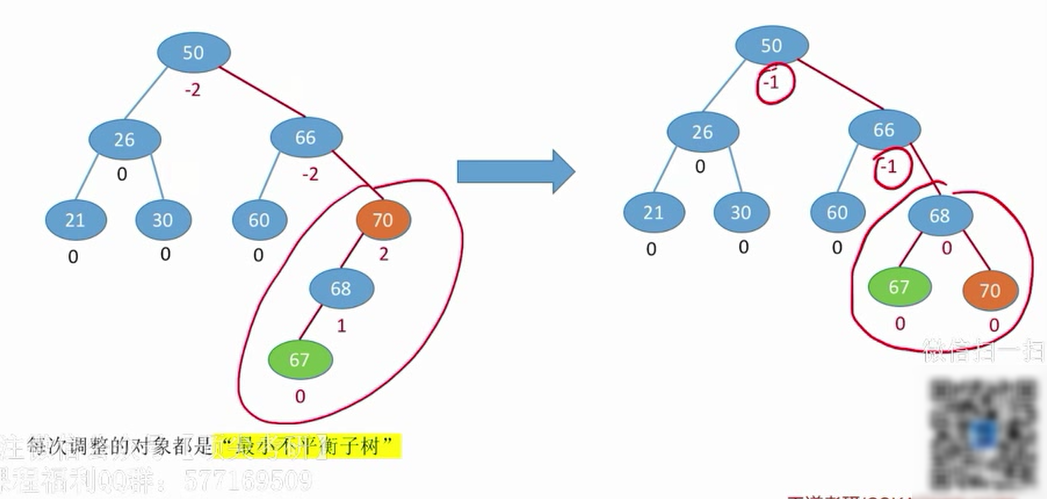
在插入操作中，只要将最小不平衡子树调整平衡，则其他祖先结点都会恢复平衡。

如何调整最小不平衡子树？

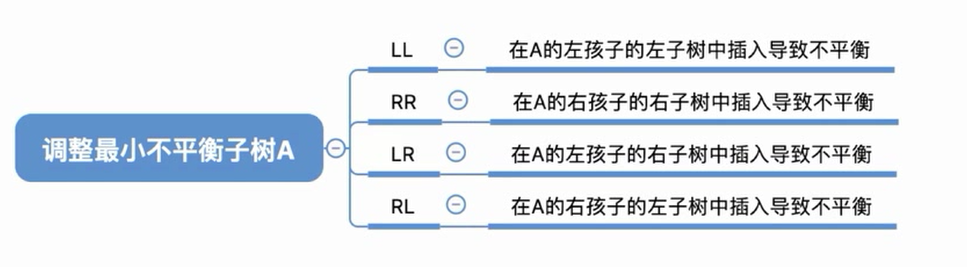
LL

(左孩子的左子树中插入导致不平衡)

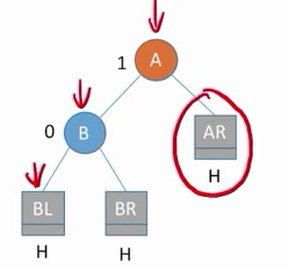
主要是因为要a是最小不平衡子树。

插入之后目标：

1. 恢复平衡
2. 保持二叉树的特性

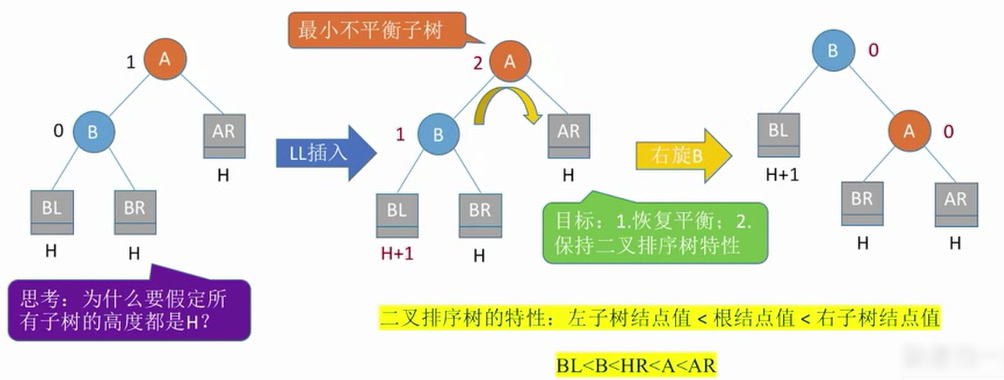
二叉排序书的特性：左子树结点值<根节点值<右子树结点值

BL<B<BR<A<AR

LL平衡旋转（右单旋转）。

RR

(右孩子的右子树中插入导致不平衡)

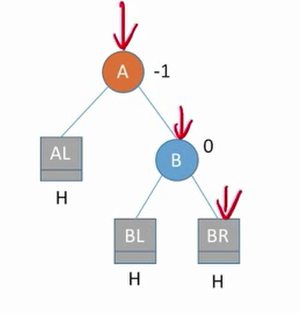
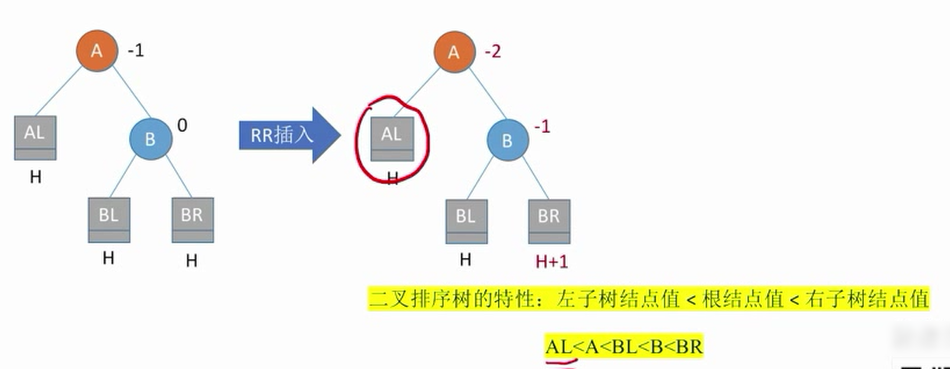
左旋操作

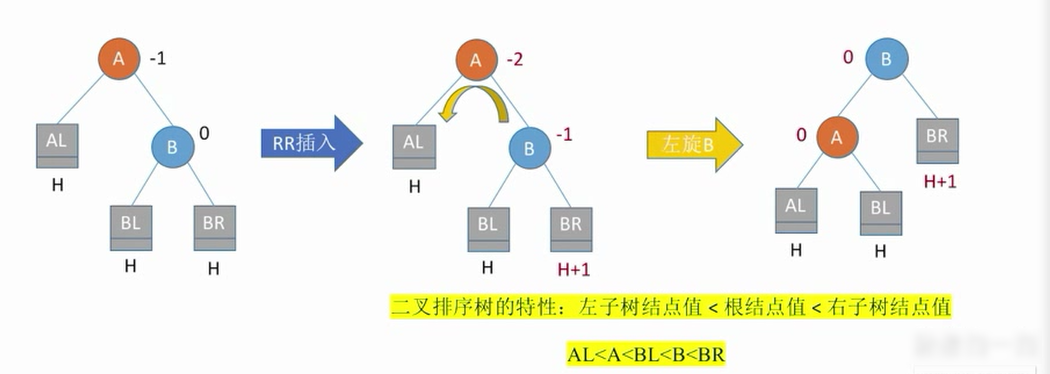
代码思路

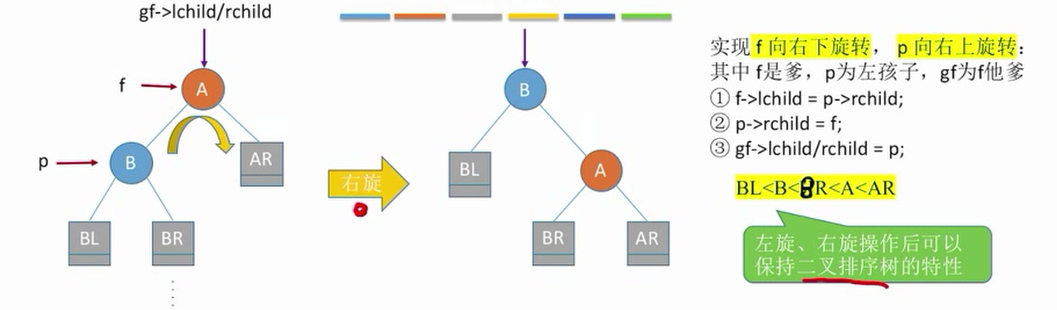
实现f向右下旋转，p向右上旋转：

其中f是爹，p是左孩子，gf是f他爹

1. f->lchild = p->rchild;
2. p->rchild = f;
3. gf->lchild/rchild = p

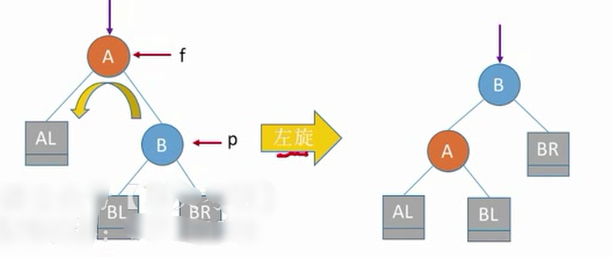
实现f向左下旋转，p向左上旋转：

其中f是爹，p右孩子，gf是f他爹

1. f->rchild = p->lchild;
2. p->lchild = f;
3. gf->lchild/rchild = p

LR

(在左孩子的右子树中插入导致不平衡)

需要把b的右子树展开

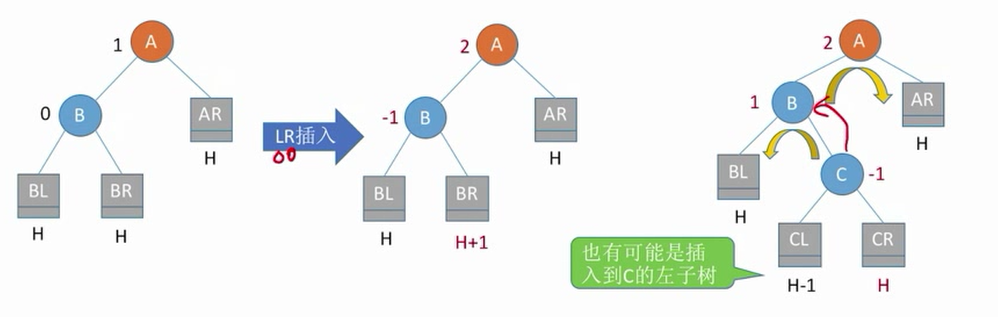
需要先把c左旋转到b的位置，在右旋转到a的位置。

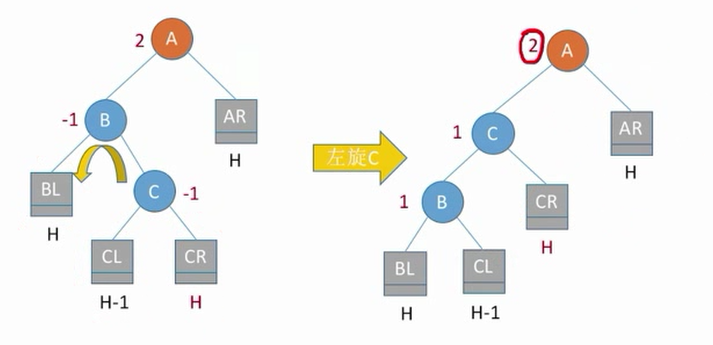
RL

（在右孩子的左子树插入了新的结点导致不平衡）

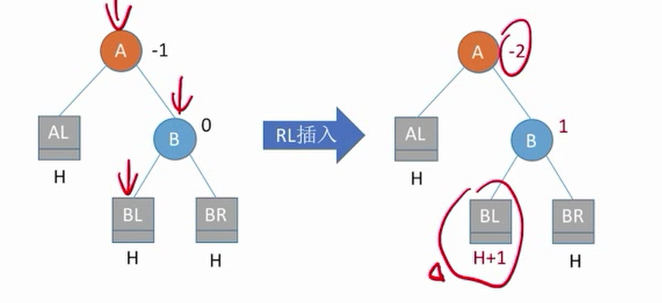
需要把b的左子树展开

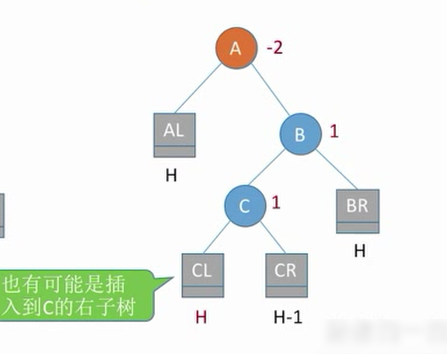
c右旋顶替b，左旋顶替a

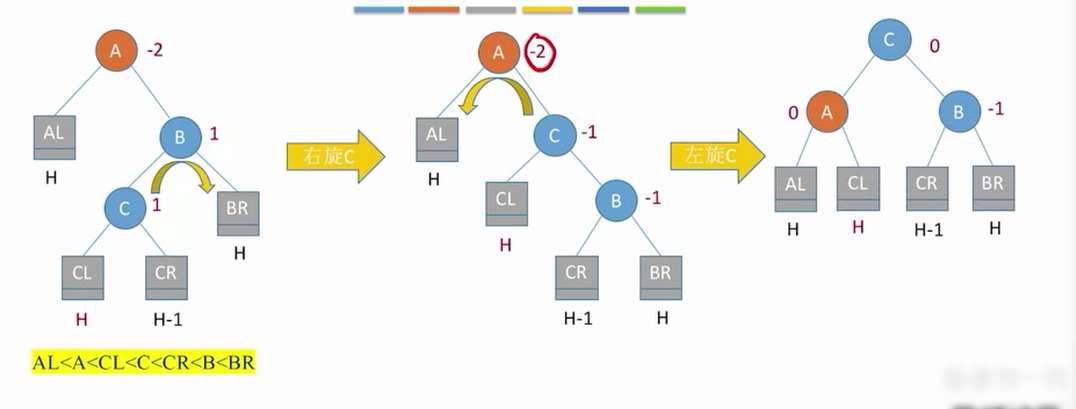
汇总

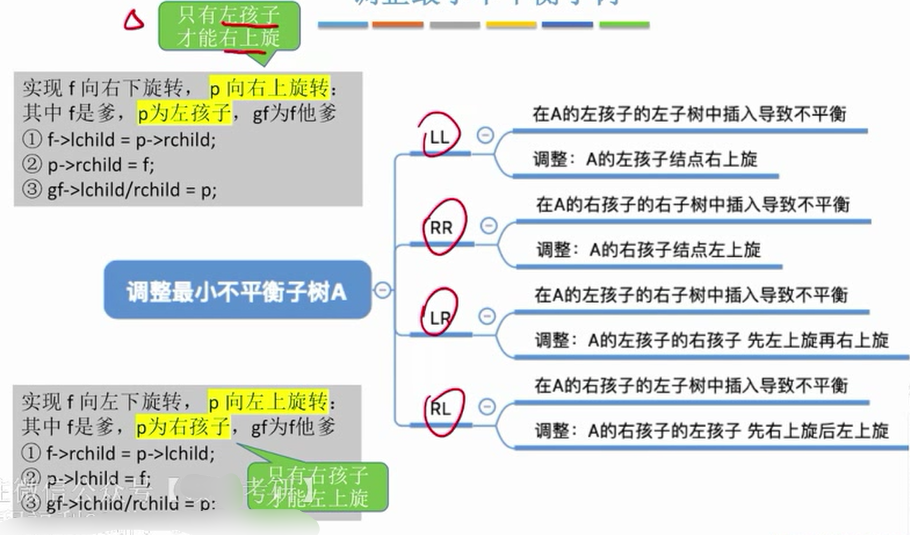
为什么只要调整最小不平衡子树？

因为插入操作导致“最小不平衡子树”高度+1，经过调整后高度恢复。

先看看树的平衡因子

找到最小平衡子树

判断是哪种型

进行操作

查找效率分析

ASL

若树高h，则最坏情况下，查找一个关键字最多需要对比h次，即查找操作时间复杂度不可能超过O(h)

其实就是分析平衡二叉树的高度有多高

平衡二叉树——树上任意一个结点的左子树和右子树之差不超过1

假设以n_h表示深度为h的平衡术，含有的最少结点数

若有n_0=0,n_1=1,n_2=2，并且有

[n_h = n_{h-1} +n_{h-2} + 1 ]

所以时间复杂度有

[O(log_2n) ]