皮尔逊相关系数及其MATLAB实现
一、参考链接
1.http://blog.csdn.net/wsywl/article/details/5727327
2.http://www.cnblogs.com/zhangchaoyang/articles/2631907.html
3.http://blog.sciencenet.cn/blog-479412-641317.html
二、初稿时间
2020年1月13日
三、皮尔逊相关系数
1. 什么是相关系数?为什么会有相关系数?
相关系数是用以反映变量之间相关关系密切程度的统计指标,相关系数的平方称为判定系数。
2. 相关系数的几种类型
相关关系是一种非确定性的关系,相关系数是研究变量之间线性相关程度的量。由于研究对象的不同,相关系数有如下几种定义方式:
(1)简单相关系数:又叫皮尔逊相关系数或线性相关系数,一般用字母P 表示,是用来度量变量间的线性关系的量。
(2)复相关系数:又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如,某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。
(3)典型相关系数:是先对原来各组变量进行主成分分析,得到新的线性关系的综合指标,再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。
3. 相关系数的性质
相关系数的值介于–1与+1之间,即–1≤r≤+1。其性质如下:
-
当|r|=1时,表示两变量为完全线性相关,即为函数关系。
-
当r=0时,表示两变量间无线性相关关系。
-
当0<|r|<1时,表示两变量存在一定程度的线性相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱。
-
一般可按三级划分:|r|<0.4为低度线性相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关。
4. 相关系数适用范围
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1) 两个变量之间是线性关系,都是连续数据。
(2) 两个变量的总体是正态分布,或接近正态的单峰分布。
(3) 两个变量的观测值是成对的,每对观测值之间相互独立。
5. 皮尔逊相关系数的计算公式
皮尔逊相关也称为积差相关(或积矩相关)是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。
假设有两个变量X、Y,那么两变量间的皮尔逊相关系数可通过以下公式计算:
公式一:
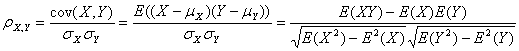
公式二:

公式三:
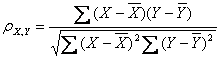
公式四:

以上列出的四个公式等价,其中E是数学期望,cov表示协方差,N表示变量取值的个数。
6. 相关系数的检验
置信度 = 1 - 显著性水平,置信度越高(显著性水平越低)说明我们越有把握相信两者相关。
四、程序实现
1. MATLAB中自带的相关系数计算函数
%*************************************************************************%
%程序目的:学习理解简单相关系数,学习MATLAB中和简单相关系数相关的函数
%2017年01月13日
%------------------经验积累S---------------------%
%(1)MATLAB中的corr函数是按照列进行相关系数计算的,所以函数的输入变量要确保至少
%2列,每列至少2个元素(1*n和1*n的向量是无法计算相关系数的)
%(2)corrcoef也可以计算相关系数,但是corrcoef计算相关系数时自动把m*n矩阵,变为
%向量,具体参考函数文档说明
%(3)corr函数默认计算的是Pearson相关系数
%(4)reshape函数用于矩阵的重塑
%------------------经验积累E---------------------%
%*************************************************************************%
clc;
clear all;
X = [1,6,7,14,13,28,31,43,55,68,77,87];
Y = [2,3,9,15,12,34,32,44,56,72,74,81];
Z = [X',Y'];
% 比较PCor1和PCor2,理解corr函数是如何按照列计算相关系数的
PCor1 = corr(X',Y');
% disp(['PCor1 = ',num2str(PCor1)]);
PCor2 = corr(Z);
% 比较corrcoef的计算结果和corr计算结果的差异
PCor3 = corrcoef(X',Y');
PCor4 = corrcoef(Z);
% 加入显著性水平P
[PCor5,P5] = corr(X',Y');
[PCor6,P6] = corr(Z);
% 通过此处进一步理解corr按列计算相关系数
K = rand(12,2).*10; L = rand(12,2).*10;
M = [Z,K]; N = [Z,L];
[PCor7,P7] = corr(M,N);
% 比较corrcoef和corr的计算结果,理解corrcoef的计算方式
[PCor8,P8] = corrcoef(M,N);
M2 = reshape(M,[],1);
N2 = reshape(N,[],1);
[PCor9,P9] = corrcoef(M2,N2);
[PCor10,P10] = corr(M2,N2);