Dijkstra算法与堆（C++）

Dijkstra算法用于解决单源最短路径问题，通过逐个收录顶点来确保已收录顶点的路径长度为最短。

    

图片来自陈越姥姥的数据结构课程：https://mooc.study.163.com/learn/1000033001?tid=1000044001#/learn/content?type=detail&id=1000112011&cid=1000126096

Dijkstra算法的时间复杂度，取决于“V=未收录顶点中dist最小者”的算法。这一步可以用线性查找实现，也可以用最小堆实现。

线性查找的算法就不用多说了。最小堆的算法有一个问题：最小堆是以未收录顶点的dist作为key来建立的，但是每一轮循环都会把部分顶点的dist值改变，也就会破坏最小堆的有序性，怎么解决？

显然应该在每一轮循环中把最小堆重新调整成有序。现在问题又来了：

1. 复杂度还合算吗？

建堆的时间复杂度是O(N)，pop一个元素的时间复杂度是O(logN)；线性查找的时间复杂度也是O(N)。建堆还额外使用了O(N)的空间。

看似一点都不合算。但我又想到每一轮循环中的建堆操作，很可能只需要调整少量元素，而对于其他元素，只需要进行访问。然而线性查找连调整都不需要，只有交换。再然而，循环过程中堆会变小，使建堆的时间复杂度中的常数变小。至于到底哪个更快，还得实践出真知。

所以只能从消除建堆操作入手。这样又是另一种算法了，参考资料[1]给出了详细说明，这种算法中每一轮的时间复杂度为O(logN)，总时间复杂度为O(|E|log|V|)（V为顶点，E为边）。

2. 如何利用STL进行堆操作？

STL <algorithm> 头文件提供了 std::is_heap 、 std::is_heap_until （这两个需要C++11）、 std::make_heap 、 std::push_heap 、 std::pop_heap 和 std::sort_heap 等函数模板用于堆操作。

现有一道单源最短路径的题：https://pintia.cn/problem-sets/994805342720868352/problems/994805523835109376，Dijkstra算法的变形而已。

以下为实现代码。三种算法用宏定义选择，已选择优先队列算法。

#include <iostream>
#include <limits>
#include <vector>
#include <queue>
#include <algorithm>
#include <utility>
#include <functional>

//#define LINEAR
//#define HEAP
#define QUEUE

struct Path
{
    Path() = default;
    Path(int _city, int _dist)
        : city(_city), dist(_dist)
    {
        ;
    }
    int city;
    int dist;
    bool operator<(const Path& _rhs) const
    {
        return dist < _rhs.dist;
    }
    bool operator>(const Path& _rhs) const
    {
        return dist > _rhs.dist;
    }
};

struct City
{
    std::vector<Path> paths;
    int team;
    int dist = std::numeric_limits<int>::max();
    bool collected = false;
    int team_max = 0;
    int dist_count = 0;
};

#ifdef HEAP
class Comparator
{
public:
    Comparator(std::vector<City>& _cities)
        : cities_(&_cities)
    {
        ;
    }
    bool operator()(int _lhs, int _rhs)
    {
        return (*cities_)[_lhs].dist > (*cities_)[_rhs].dist;
    }
private:
    std::vector<City>* cities_;
};
#endif

int main()
{
    int n, m, src, dst;
    std::cin >> n >> m >> src >> dst;
    std::vector<City> cities(n);
    for (auto& city : cities)
        std::cin >> city.team;
    for (int cnt = 0; cnt != m; ++cnt)
    {
        int src, dst, dist;
        std::cin >> src >> dst >> dist;
        cities[src].paths.emplace_back(dst, dist);
        cities[dst].paths.emplace_back(src, dist);
    }

    {
        auto& city = cities[src];
        cities[src].collected = true;
        cities[src].dist = 0;
        cities[src].dist_count = 1;
        cities[src].team_max = cities[src].team;
    }
#ifdef QUEUE
    std::priority_queue<Path, std::vector<Path>, std::greater<Path>> queue;
#endif
    for (const auto& path : cities[src].paths)
    {
        cities[path.city].dist = path.dist;
        cities[path.city].dist_count = 1;
        cities[path.city].team_max = cities[src].team + cities[path.city].team;
#ifdef QUEUE
        queue.emplace(path.city, path.dist);
#endif
    }

#ifdef HEAP
    std::vector<int> heap;
    heap.reserve(n - 1);
    for (int i = 0; i != n; ++i)
        if (i != src)
            heap.push_back(i);
    Comparator comp(cities);
    std::make_heap(heap.begin(), heap.end(), comp);
#endif

    while (1)
    {
#ifdef LINEAR
        int min_dist = std::numeric_limits<int>::max();
        int index = -1;
        for (int i = 0; i != n; ++i)
            if (!cities[i].collected && cities[i].dist < min_dist)
                min_dist = cities[i].dist, index = i;
        if (index == -1)
            break;
        auto& city = cities[index];
#endif
#ifdef HEAP
        if (heap.empty())
            break;
        auto& city = cities[heap[0]];
#endif
#ifdef QUEUE
        if (queue.empty())
            break;
        Path temp;
        while (1)
        {
            temp = queue.top();
            queue.pop();
            if (!cities[temp.city].collected)
                break;
        }
        auto& city = cities[temp.city];
#endif
        city.collected = true;
        for (const auto& path : city.paths)
        {
            if (!cities[path.city].collected)
            {
                auto& dest = cities[path.city];
                if (city.dist + path.dist < cities[path.city].dist)
                {
                    dest.dist = city.dist + path.dist;
                    dest.dist_count = city.dist_count;
                    dest.team_max = city.team_max + dest.team;
                }
                else if (city.dist + path.dist == cities[path.city].dist)
                {
                    dest.dist = city.dist + path.dist;
                    dest.dist_count += city.dist_count;
                    if (city.team_max + dest.team > dest.team_max)
                        dest.team_max = city.team_max + dest.team;
                }
#ifdef QUEUE
                queue.emplace(path.city, dest.dist);
#endif
            }
        }
#ifdef LINEAR
        if (index == dst)
            break;
#endif
#ifdef HEAP
        if (heap[0] == dst)
            break;
        std::pop_heap(heap.begin(), heap.end(), comp);
        heap.pop_back();
        std::make_heap(heap.begin(), heap.end(), comp);
#endif
#ifdef QUEUE
        if (temp.city == dst)
            break;
#endif
    }

    {
        auto& city = cities[dst];
        std::cout << cities[dst].dist_count << ' ' << cities[dst].team_max;
    }

    return 0;
}

测试结果：

线性查找版

最小堆版

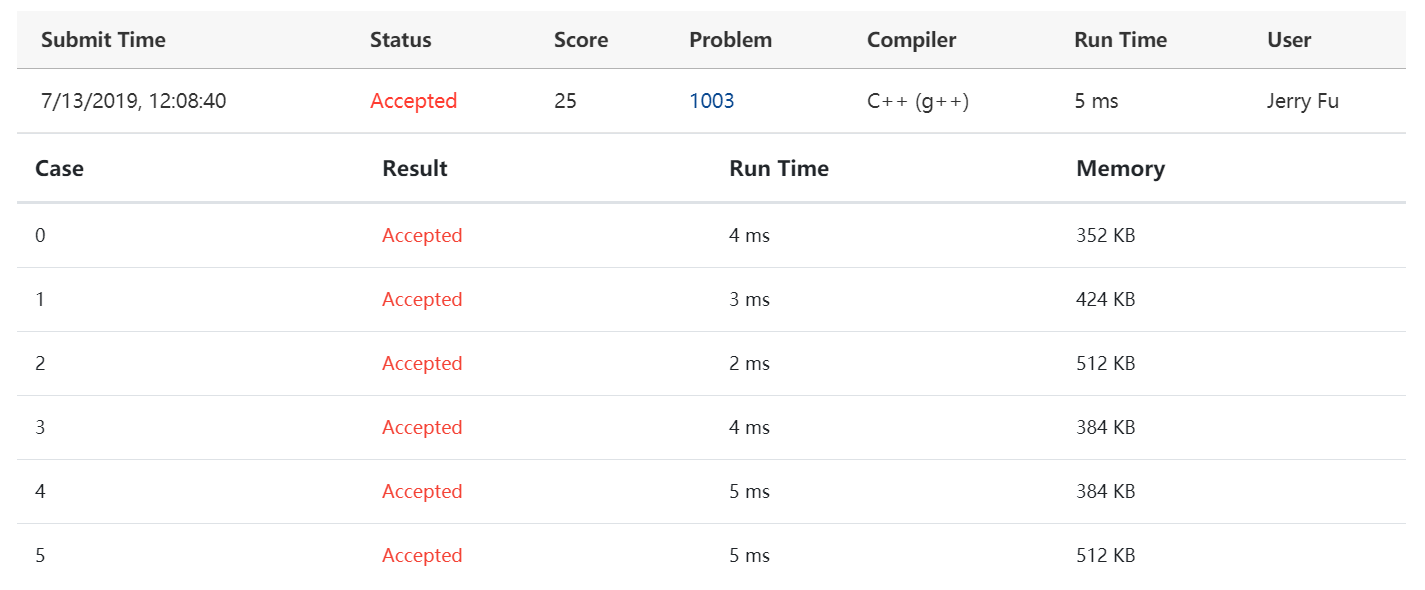
优先队列版

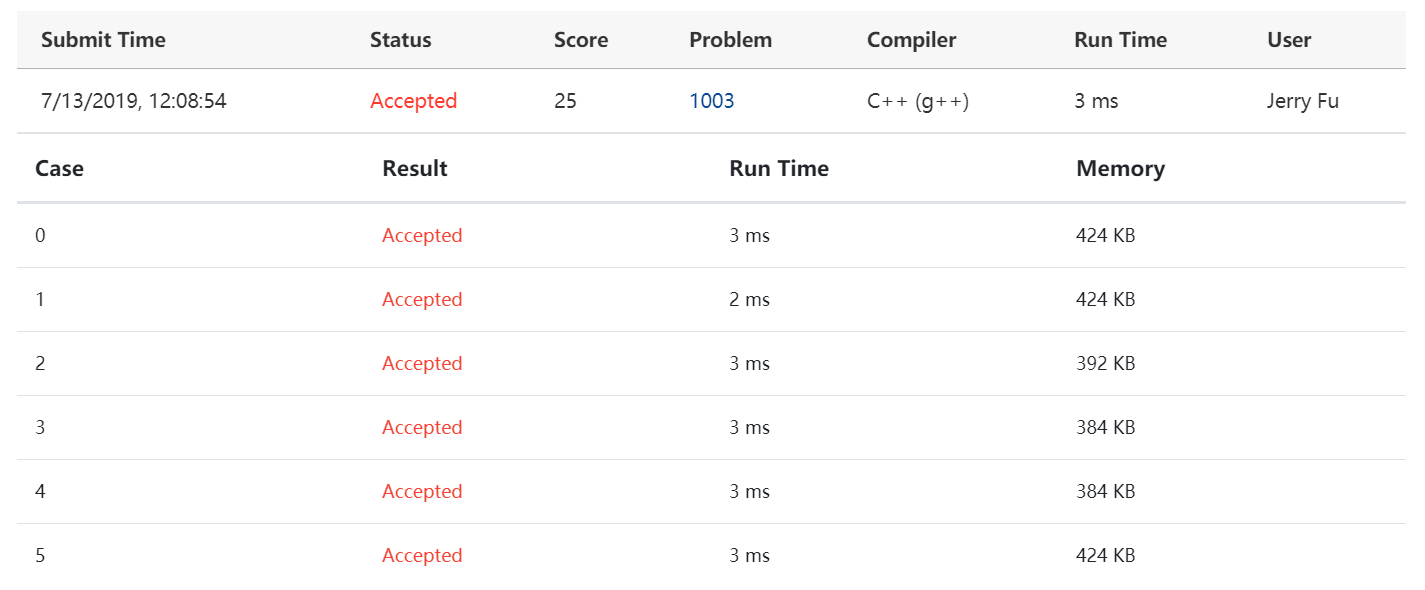
平台显示线性查找版的时间6ms，内存512KB；最小堆版的时间5ms，内存512KB；优先队列版的时间3ms，内存424KB。我认为时间都太短了，数据量不够大，不足以说明问题。

如果仅从理论上分析的话，我认为优先队列的算法是最优的。

参考资料：

[1] dijkstra + heap 优化 https://blog.csdn.net/sentimental_dog/article/details/51955765