1.本周学习总结(0--2分)
1.1思维导图

1.2.谈谈你对图结构的认识及学习体会。
图的学习中,要注意的有很多。图中数据元素叫做顶点。
在图中,不允许没有顶点。若 V 是图的顶点的集合,那么,V 是非空有穷集合。
图的任意两个顶点之间都可能有关系,它们的关系用边来表示。边集可以是空的。
无向边、无向图、有向边、有向图、简单图。图的存储结构,在图的学习过程中也是比较难理解的。
图的邻接矩阵存储方式是用两个数组表示图,数组与链表相结合的方法称为邻接表。
总的来说最近学习太紧了,马上要期末考了,代码作业又比较多,感觉快学不过来了。
2.PTA实验作业(6分)
2.1.题目1:题目名称
7-1 图着色问题
2.1.1设计思路(伪代码)
建立邻接矩阵g
将颜色存入到数组a[]中
for i=1 to i=n
for j=1 to j=n
if(if(a[i]==a[j]&&g[i][j]==1) flag=0 //对于每一个条边g[i][j],其两个顶点的颜色分别位a[i]和a[j],若有a[i]=a[j],则可判断不满足条件
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
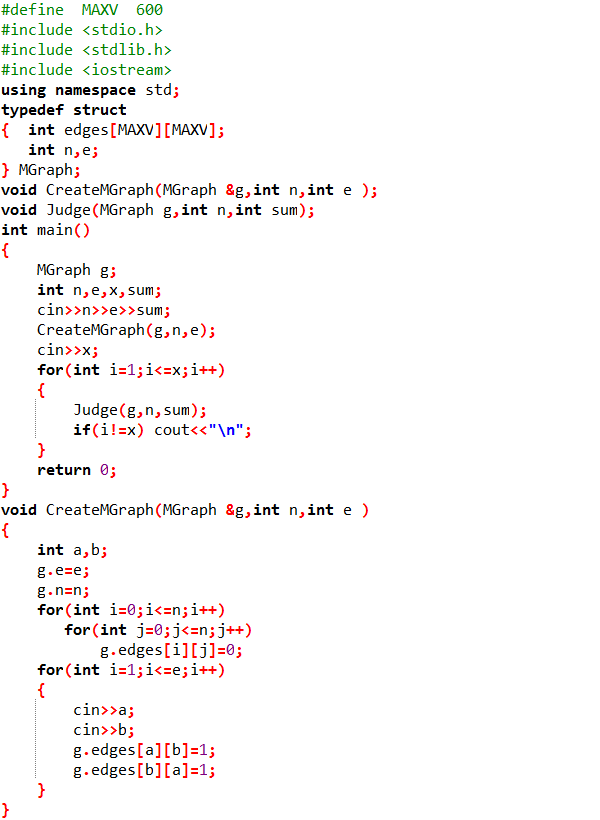
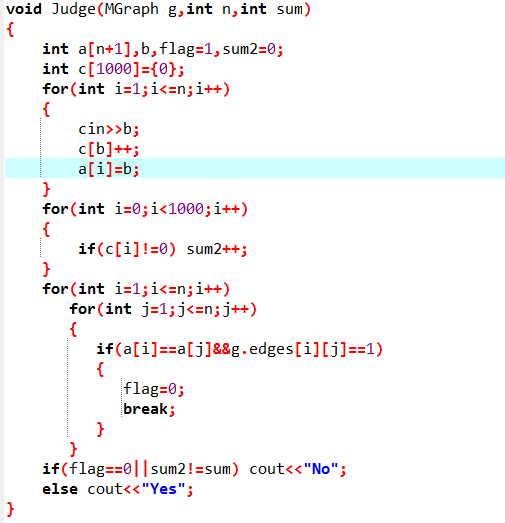
2.1.3本题PTA提交列表说明。

Q1:要求颜色数要等于输出的颜色数这一个我没有注意到
2.2 题目2
7-3 六度空间
2.1.1设计思路(伪代码)
建立邻接表g,遍历g
visited[]判断结点,访问为1,否为0
q.push(x)//先将x放入队列中
visited[x]=0;
while(!q.enmpty())//当q不为空时
{
temp=q.front();
p访问q中队头所对应的邻接表结点
q.pop();
while(p!=NULL)
{
如果p未被访问 {入队,这样子当访问到最后该层的最后一个结点时,储存的会是下一层最后一个结点的位置 }
p=p->nextarc 访问p的下一个邻接点
}
if(temp=last) 此时找到了下一层结点的最后一个元素位置,将其值给last}
}
return sum
2.2.2代码截图

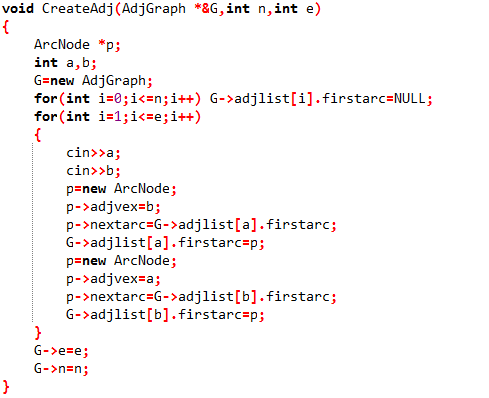
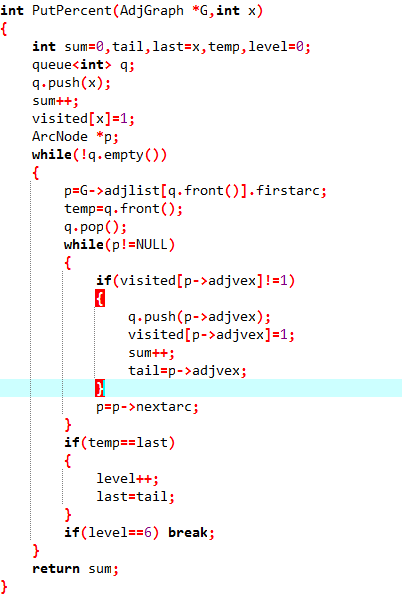
2.2.3本题PTA提交列表说明。

Q1:按照书上和mooc上的视频学习了一下,有些测试点过不去具体还是同学的帮助下完成的
2.3 题目3
7-4 公路村村通
2.3.1设计思路(伪代码)
最小堆存边结点,然后直接用kruskal建最小生成树的思想累计成本,用并查集判断结点间是否连通
就是对每一个已经入队的点一个一个遍历寻找下一个最短路径
但是 更好的方法是对每一个点入队 更新到未入队的点的最短距离 就是 距离比原先的距离小 就更新 这样每次对每个点更新那么就能保证lowCost中的距离在当前状态下就是最小的
然后每次让距离最短的入队就可以了
2.3.2代码截图



2.3.3本题PTA提交列表说明

Q:一开始我自己写的最小生成树超时了
3、上机考试错题及处理办法(-2--2分)
3.1.截图错题代码

3.2 错的原因及处理方法
这一道题主要是打了好久,一个点都没有过去,后面就输出了个-1来拿个分。主要的思路就是上面讲的
用最小堆存边结点,然后直接用kruskal建最小生成树的思想累计成本,用并查集判断结点间是否连通。考试的时候在前面的题卡主太久,主要也是自己图这一块学的不太好,
导致自己时间花的太多,后面的时间不够我去进行,调试修改,时间不太够我去完成。