【笔记】最短路学习

最短路自学笔记

---

最短路问题常见于生活以及各大OI中，用处广泛。所以最短路问题十分重要。

首先我们要了解最短路问题的基本思路：

基本思路：

1. Floyd的基本思路是枚举中转站，看看中转站和原先的路径长度和与中转以后的路径长度和那一个更短，进行更新。

2. Dijkstra的算法思想：①将一开始所有的非源点到源的距离设置成无限大（你认为的无限大实际上是0x3f(int)或者0x7fffffff(long long)），然后源到源距离设置成0（不就是0吗），然后每次找到一个距离源最短的点u，将其变成白点，枚举所有的蓝点，如果源到白点存在中转站——一个蓝点使得源->蓝点和蓝点->白点的距离和更短，就更新。②每找到一个白点，就尝试更新其他蓝点，直到更新完毕。

   写一个伪代码理解一下：

   const int maxn=10001;//邻接矩阵存储
   bool color[maxn];//判断颜色用的
   int dis[maxn],mp[maxn][maxn];//假设1是源
   dis[1]=0,mp[i][j]=0x7ffff,mp[i][i]=0;//(i!=j)
   while (有蓝点)
   {
       u=最近的蓝点;
       color[u]=true;//白了
       for (register int i=first[i];i!=0;i=next[i])
       {
           if (dis[i]>dis[u]+w[u][i])
               dis[i]=dis[u]+w[u][i];
       }
   }
   

3. Bell-Manford算法

4. SPFA对BF的队列优化算法

---

一、Floyd的代码实现

不多说了吧，直接上代码：

for (register int k=1;k<=n;k++)
    for (register int i=1;i<=n;i++)
        for (register int j=1;j<=n;j++)
            if (dis[i][j]>dis[i][k]+dis[k][j])
                dis[i][j]=dis[i][k]+dis[k][j];

二、Dijkstra的代码实现

我们刚才没说如何判断所有点都已经遍历：

控制一个k，使得原先初值k=0，查一遍若......k=更新的点，k如果还=0，就break;。

上代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;
typedef long long int lli;
int mp[1001][1001],dis[1001],n,m,min1,k;
bool visit[1001];
const lli INF=0x7fffffff;
int main()
{
    cin>>n>>m;
    memset(mp,0xffff,sizeof(mp));
    memset(dis,0xffff,sizeof(dis));
    dis[1]=0,visit[1]=true;
    memset(visit,false,sizeof(visit));
    for (register int i=1;i<=n;i++)
    {
        mp[i][i]=0;
    }
    for (register int i=1;i<=m;i++)
    {
        int from,to,value;
        cin>>from>>to>>value;
        mp[from][to]=value;
    }
    for (register int i=1;i<=n-1;i++)
    {
        min1=INF;
        k=0;
        for (register int j=1;j<=n;j++)
        {
            if (!visit[j]&&dis[j]<min1)
            {
                min1=dis[j];
                k=j;
            }
        }
        if (k==0)break;
        visit[k]=true;
        for (register int j=1;j<=n;j++)
        {
            if (dis[k]+mp[k][j]<dis[j])
                dis[j]=dis[k]+mp[k][j];
        }
    }
    cin>>n;
    for (register int i=1;i<=n;i++)
    {
        int to;
        cin>>to;
        cout<<dis[to];
    }
    return 0;
}

我们考虑一下对它的优化。因为如果我们每一次都要扫一遍判断出边，我们还不如直接存出边：

邻接表！（链式前向星）

好东西。

缺点：O(1)访问没了。

先看一个图（可能会长这样）：

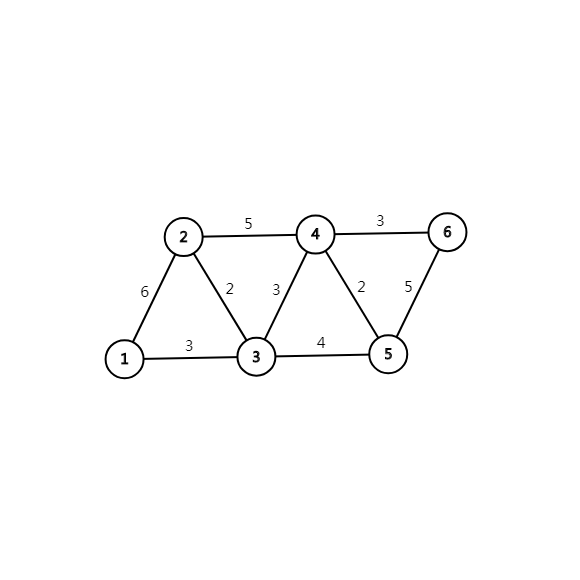
我们这样存图：

struct edge{
    int to,value,next;
}gragh[200001];
int head[100001],dis[100001],n,m,cnt,num=0;
void add(int x,int to,int value)
{
    num++;
    gragh[num].to=y;
    gragh[num].next=head[x];
    gragh[num].value=value;
    head[x]=num;
}

然后我们用扫描出边的方式而不是遍历所有点。

上代码：

#include <bits/stdc++.h>
using namespace std;
const int MAXN=100010;
const int MAXM=200010;
const int INF=2147483647;
int n,m,s,x,y,z,num;
int dis[MAXN],head[MAXM];
bool vis[MAXN];
struct EDGE
{
    int to;
    int w;
    int next;
}ed[MAXM];
struct node
{
    int dis;
    int pos;
    inline friend bool operator < (const node &x,const node &y)
    {
        return x.dis < y.dis;
    }
};
void add(int x,int y,int z)
{
    num++;
    ed[num].to=y;
    ed[num].next=head[x];
    ed[num].w=z;
    head[x]=num;
}
void dijkstra(int s)
{
    priority_queue<node>q;
    for(int i=1;i<=n;i++) 
    {
        dis[i]=INF;//设置成无限大
        vis[i]=true;//设置成没有遍历
    }
    dis[s]=0;//设置s为源
    q.push((node){0,s});
    while(!q.empty())
    {
        node w=q.top();
        q.pop();
        int x=w.pos;
        if(vis[x])
        {
            vis[x]=false;
            for(int i=head[x];i;i=ed[i].next)
            {
                int y=ed[i].to;
                dis[y]=min(dis[y],dis[x]+ed[i].w);
                q.push((node){dis[y],y});
            }
        }
    }
}

链式前向星+堆优化真心好用qwq。