Day 4 学习笔记 各种图论
图是什么????
不是我上传的图床上的那些垃圾解释...
一、图:
1.定义
由顶点和边组成的集合叫做图。
2.分类:
边如果是有向边,就是有向图;否则,就是无向图。
平常的图一般都有标号,我称之为标号的图(废话)有序图,如果没有标号,就称之为无序图(没标号的图)
注意有向图和无向图转换之后可能不同,然后有序图和无序图转换之后也不同。
3.存储方式
1.基础方式:邻接矩阵
优点:O(1)查询,
缺点:O(n^2)存储

这个图很好的 解释了邻接矩阵的情况。
如果是有向图,可以这样存;无向图就是上下对称的方式记录。
2.链式前向星(模拟链表)
优点:遍历所有出边
缺点:O(1)的询问没了
struct edge{
int from,to,dis,next;
} Edge[100001];
//从哪里来,指向哪里,出边的第一条边,上一条出边的标号
//就像单向链表向头部添加元素一样
//当然,用vector存储也可以
如何添一条边呢?
很明显有两种情况,如果是一开始没有边,就只改first和添的边的next改成0,然后把边的权值改上。如果有边,就塞到最后面。
代码实现:
int cnt=1,head[10086];//当前是第几条要加上的边,以及10085条链表的头部
inline void add_edge(int from,int to,int dis)
{
Edge[cnt]=(edge){from,to,dis,head[from]};
head[from]=cnt++; //更新头部
}
二、最短路问题
解决方式十分多(复杂)的问题。
1.Floyd算法(dp)(支持负边权)
for (register int i=1;i<=n;i++)
for (register int j=1;j<=n;j++)
f[i][j]=a[i][j];
for (register int k=1;k<=n;k++)
for (register int i=1;i<=n;i++)
for (register int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
令人窒息的O((n^3))和S((n^2)). . . . . .
因为是...简单的求和,所以可以有负边权!(真好)
2.bellman-ford算法
核心:松弛操作。
for (register int i=1;i<=n;i++)
f[i]= INF
for (register int i=1;i<=n;i++)
{
for (register int j=1;j<=m;j++)
{
if (Edge[i].from=i)
{
int to=Edge[i].to;
dis[to]=min(dis[from]+Edge[i].dis,dis[to]);
}
}
}
SPFA 队列优化:
核心:队列方式优化,更新dis值
求初始点到任意一点的值。
就是先开一个队列,然后更新与这个点有关的值,然后出队,然后再次用更新的进去的元素,就更新,然后更新,出队,入队......反复操作......直到队列里没东西了。
队列中就是所谓的白点,而队列外面就是所谓的蓝点。
一个点如果更新了其他的点,那么其他的点就将成为白点,而这个点就将回到蓝点的行列中。被更新的点由于更加优化,所以有可能会再去更新其他的点。
queue<int> qwq;
for (register int i=1;i<=n;i++)
dis[i]=INF;
dis[S]=0; //自己到自己=0
vst[S]=true; //源点将先成白色的
qwq.push(S); //将源点先塞进去
while (!qwq.empty())
{
int now=qwq.front();
qwq.pop();
vst[now]=false; //回归蓝点的行列
for (int i=head[now];i;i=Edge[i].next)
{ //遍历以now为起点的边的链
int to=Edge[i].to;//终点
if (dis[to]>dis[now]+Edge[i].dis)//如果距离可以缩减
{
dis[to]=dis[now]+Edge[i].dis;//当然还是缩减了好
if (!vst[to]) //如果还不是白点
{
qwq.push(to);//压进队列
vst[to]=true;//就染色成为白的
}
}
}
}
3.Dijkstra 算法
巨贪无比的算法......(邻接矩阵可用)
基本原理:Dijkstra算法采用的是一种贪心的策略。
首先有一些要开的数组,存一些数据,并且初始化操作。
int dis[maxn]={0},m,n,edge[maxn][maxn];
//声明一个数组dis来保存源点到各个顶点的最短距离
//初始时,原点 s 的路径权重被赋为 0 (dis[s] = 0)。
//edge[maxn][maxn]邻接矩阵表示边
bool visit[maxn];
//和一个保存已经找到了最短路径的顶点的数组visit。
void input()
{//输入数据
memset(edge,+OO,sizeof(edge));
scanf("%d%d",&n,&m);
int x,y,z;
for (register int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
edge[x][y]=z;
}
}
Dijstra的方式类似一种dp,采用更新每个点最短路的思想,但是是从一点出发的更新,这是和floyd的不同,这也是Dij只能跑单源最短路问题的根本原因。
因为一开始源点和源点距离是0,知道它的出边,所以把自己到自己更新成+OO,然后把所有出边到达点的距离都更新一个遍,剩下的就全部设置成+OO。
void init(int firstp)
{//初始化
memset(dis,+OO,sizeof(dis));//define +OO 0x7f
dis[firstp]=0;
for (int i=1;i<=n;i++)
if (edge[firstp][i]!=+OO)
dis[i]=edge[firstp][i];
}
/*
初始时,visit只有源点p是true,
然后,从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,
并且把该点加入到T中,此时完成一个顶点,
然后,我们需要看看新加入的顶点是否可以到达其他顶点,
并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,
如果是,那么就替换这些顶点在dis中的值。
然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。*/
void dijkstra()
{
while(!q.empty())
{
int lp=q.top().second;
q.pop();
if (visit[lp])continue;
visit[lq]=true;
for (int e=first[lp];e;e=next[e])
if (dis[to[e]]>dis[lp]+value[e])
{
dis[to[e]]=dis[lp]+value[e];
q.push(make_pair(dis[to[e]],to[e]));
}
}
}
三、最小生成树
真好啊,第一次使用最小生成树(逃)
一个有n个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边权。
这玩意听着咋这样珂幻?
首先我们经过一些珂幻的证明可以得出——最小生成树性质:
设 G=(V,E)是一个连通网络,U是顶点集V的一个非空真子集。若(u,v)是G中一条“一个端点在U中(例如:u∈U),另一个端点不在U中的边(例如:v∈V-U),且(u,v)具有最小权值,则一定存在G的一棵最小生成树包括此边(u,v)。
——摘自百度百科

这个性质有什么用呢?
别急。首先,我用汉语翻译一下刚刚那个百度百科上展示的中国珂学院展示的数学集合语言:首先我们有一个图叫G,然后我们用来存所有点的集合set叫V,存所有边的集合叫E(Edge) ,U是V的一个非空真子集,就是不完全包含V的存点的set集合U,这两个东西之间在图内存在一条边,一个端点在U,另一个端点不在U,这条边就必定是最小生成树的组成部分。
还是没啥感觉? 那待会就看下面的LCA部分。
4.Kruskal 算法
怎样实现最小生成树呢?
第一个算法就是Kruskal 算法。
算法的核心思想还是贪心(巨贪无比)。我们已经讲过优先队列(详见Day 3 STL模板库笔记),只需要用优先队列存一些边的集合...
是不是有点思路了?(并没有)
所以,要进行的操作是:
- 输入数据
- 初始化:(V_{new}= [x])(
bool visit[......];visit[x]=true;),其中x为集合V中的任一节点(起始点),(E_{new}= [Null])(优先队列玄学操作),为空; - 反复操作以下几个操作,直到把所有的点都遍历过一遍:
好消息是:一般prim用的是邻接矩阵(太棒了!)
如果还不明白就看一个图例明白一下:

但是当图特别稀疏的时候,prim的优势就显现不出来。这时候我们用到了Kruskal算法。
Kruskal?那是什么?
同样是贪心,这个贪的是边。我们要按照边权从小到大的顺序连边。
我们还是要用到并查集(往下看四、)。
首先我们有这样一个图:
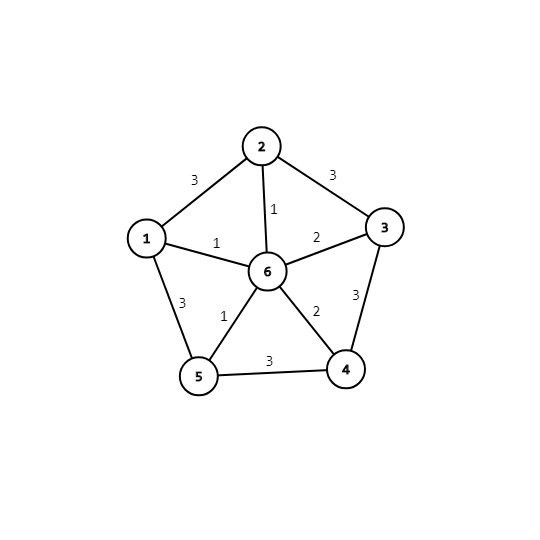
然后连边:
2->6 1 sum=1
1->6 1 sum=2
5->6 1 sum=3
4->6 2 sum=5
5->6 2 sum=7
但是注意:如果边的两侧是用一个父亲节点,那么证明连起来是一个环。
所以用到了并查集。并且还要路径压缩版。
然后我们如果遍历完所有点,那就退出来,因为所有的点都在“树”里面了。
上代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn=2*1e6+1,maxm=5*1e3+1;
struct Edge{
int from,to,value;
friend bool operator < (const Edge &a,const Edge &b)
{
return a.value<b.value;
}
}gragh[maxn];
bool vis[maxm];
int fa[maxm],num_p,num_e,sum,cnt,n,m;
inline int find(int son)
{
if (son==fa[son])return son;
else return fa[son]=find(fa[son]);
}
void kruskal()
{
sort(gragh+1,gragh+m+1);
for (register int i=1;i<=m;i++)
{
int fa_f=find(gragh[i].from);
int fa_t=find(gragh[i].to);
if (fa_f==fa_t){continue;}
sum+=gragh[i].value;
fa[fa_t]=fa_f;
if (++cnt==n-1)break;
}
}
int main()
{
cin>>n>>m;
for (register int i=1;i<=n;i++)
{
fa[i]=i;
}
for (register int i=1;i<=m;i++)
{
cin>>gragh[i].from>>gragh[i].to>>gragh[i].value;
}
kruskal();
cout<<sum;
return 0;
}
5.prim 算法
6.树上倍增算法和LCA(最近公共祖先)
Upd on 2019 7 25:
看到有这么多看这篇文章的
我就更新了最短路的那部分
剩下的最小生成树早晚要更新qwq